1.3. Геометрическое решение задач линейного программирования

Если система ограничений и целевая функция задачи линейного программирования содержат две переменные, то эту задачу можно решить геометрически.

Геометрическое решение задачи линейного программирования состоит в следующих действиях:

1. заменить в каждом ограничении знак неравенства на знак равно;

2. в прямоугольной системе построить соответствующие прямые,

3. выделить область точек на плоскости, координаты которых удовлетворяют системе ограничений (ограничению со знаком "" удовлетворяют точки, находящиеся выше прямой, а знаку "" – ниже прямой);

4. в целевой функции отбросить свободный член и построить соответствующую прямую;

5. при поиске максимума последнюю прямую параллельно перемещаем вверх, а минимума – вниз;

6. координаты точки области, которую прямая пересечёт последней, будут давать максимум (минимум) целевой функции, если эта точка существует.

Пример. Решить задачу линейного программирования:

f = x₁ + 2x₂ + 3  max

Решение.

1. Заменим в ограничениях знаки "" на знак равно, получим уравнения двух прямых:

Построим эти прямые в прямоугольной системе координат:

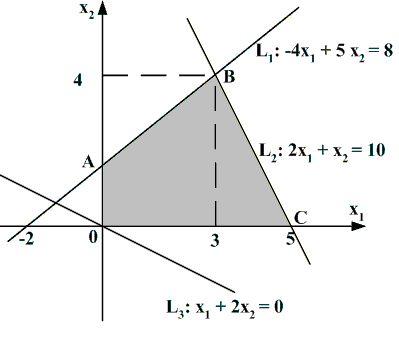
2. Выделим область точек на плоскости, координаты которых удовлетворяют системе ограничений (на рисунке эта область 0ABC закрашена):

первому ограничению удовлетворяют точки на плоскости, которые лежат ниже прямой L₁, второму ограничению – ниже прямой L₂, третьему – точки, находящиеся правее оси Ox₂, четвёртому – выше оси Ox₁

3. Отбросим свободный член в целевой функции, получим функцию y = x₁ + 2x₂, построим график этой функции (прямую L₃).

4. Перемещая прямую L₃ параллельно вверх, находим, что последней точкой области 0ABC, которую она пересечёт, будет точка B.

5. Для нахождения координат точки В решаем систему уравнений:

решение системы: x₁ = 3, x₂ = 4.

Вывод: максимальное значение целевой функции f равно 3 + 2*4 + 3 = 14 и достигается при x₁ = 3, x₂ =4.

Примечание.

Упражнения. Решить геометрически задачу линейного программирования, результат проверить в Microsoft Excel.

1. 2.

3. 4.

1.4. Симплекс-метод решения задач линейного программирования

Решение задач линейного программирования симплекс-методом осуществляется по следующему алгоритму.

1. Если требуется найти максимум целевой функции f,

то найти минимум целевой функции –f.

2. Найти любое опорное решение задачи линейного программирования.

3. Если опорное решение существует,

то

найти оптимальное (min) опорное решение;

4. Если требовалось найти максимум целевой функции,

то

умножить на -1 найденный минимум.

1.4.1. Поиск опорного решения задачи линейного программирования

1. Преобразовать систему ограничений к стандартному виду:

(1)

Примечание. Переменные слева от равенств называются базисными, а в круглых скобках – свободные.

2. Если в системе (1) все _i  0,

то

приравнять к нулю все свободные переменные и этим получить опорное решение.

3. Если в системе (1) найдётся _i < 0,

то

найти и поменять местами свободную переменную x_k и базисную переменную x_n (то есть свободную переменную x_k ввести в состав базисных, а базисную переменную x_n – в состав свободных).

4. Если обмен произвести удалось,

то

продолжить с п. 2,

иначе

опорного решения не существует.

Пример. Найти опорное решение следующей задачи линейного программирования

(2)

Решение.

1. Приводим систему ограничений к стандартному виду:

а) получаем систему линейных уравнений по правилу:

если в системе ограничений есть неравенства, то в левые части неравенств со знаком "" следует добавить новые переменные , а из левых части неравенств "" – вычесть новые переменные:

в системе ограничений (2) есть неравенства и все со знаком "", поэтому, добавляем к левым частям неравенств новые переменные:

(3)

б) Приводим систему линейных уравнений (3) к ступенчатому виду:

• записываем расширенную матрицу системы из коэффициентов при неизвестных и свободных членов:

;

• умножаем вторую строку на -1 и меняем местами первую и вторые строки:

;

• умножаем первую строку на 5 и складываем со второй, умножаем первую строку на 3 и складываем с третьей и получаем ступенчатый вид матрицы:

.

в) Приводим систему линейных уравнений к приведённому ступенчатому виду:

• первую строку умножаем на -1, третью строку делим на -3:

;

• умножаем третью строку на -3 и складываем со второй, складываем третью и первую строки и получаем приведённый ступенчатый вид матрицы:

или

или

• приводим систему к стандартному виду:

(4)

Базисные переменные: x₁, x₂ и x₃, свободные переменные: x₄, y₁, y₂ и y₃.

2. В системе (4) есть не отрицательные свободные члены, поэтому ищем для обмена свободную и базисную переменные:

• взять любое уравнение с отрицательным свободным членом,

в системе (4) берём первое уравнение;

• если во взятом уравнении нет отрицательных коэффициентов при свободных переменных, то опорного решения не существует,

в первом уравнении два отрицательных коэффициента при x₄ и y₃;

• взять любую свободную переменную с отрицательным коэффициентом и выделить столбец, содержащий взятую переменную,

возьмём переменную x₄ и выделим столбец с x₄;

			-	(					)
		9	-	(					)
			-	(					)

• в выделенном столбце найти наименьшее отношение свободных членов к коэффициентам при свободных переменных, знаки которых совпадают со знаками свободных членов,

в столбце с x₄ два коэффициента в первой и второй строках, знаки которых совпадают со знаками свободных членов, находим минимальное отношение:

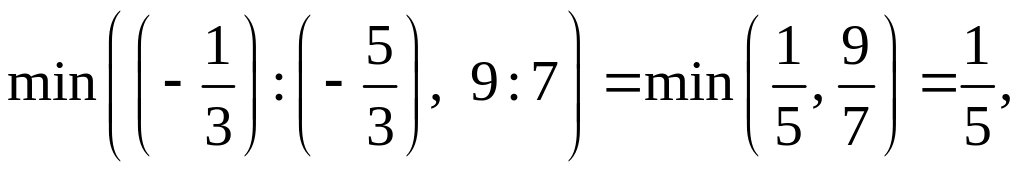
• взять базисную переменную, которая находится в строке с минимальным отношением,

минимальное отношение находится в первой строке, поэтому берём базисную переменную x₁:

			-	(					)
		9	-	(					)
			-	(					)

(выделенные столбец и строка)

• обменять местами выбранные свободную и базисную переменные, для этого:

• выразить в выбранной строке свободную переменную через все оставшиеся и подставить полученное выражение во все оставшиеся уравнения

в нашем случае меняем местами переменные x₄ и x₁:

в первой строке выражаем x₄ через оставшиеся переменные:

подставляем выражение для x₄ во второе и третье уравнения:

и получаем новый стандартный вид системы:

(5)

В этой системе все свободные члены не отрицательные, поэтому, приравнивая к нулю все свободные переменные, получим опорное решение: