2. Раздельное резервирование

При раздельном способе резервирования, вводится индивидуальный резерв для каждой части неизбыточной системы. Раздельное резервирование бывает общим и замещением. При раздельном замещении отказ системы может произойти только тогда, когда отказ дважды подряд произойдет в одном и том же устройстве, что маловероятно. Для оценки надежности при раздельном резервировании используется сложный, специфический математический аппарат. В целом, математический анализ показывает, что наиболее высокие показатели надежности можно получить в случае построения систем с использованием раздельного резервирования замещением ненагруженным резервом.

2. Использование метода статистических испытаний для расчета надежности информационных систем

   1. Сущность и обоснование метода статистических испытаний

Известные в настоящее время подходы (полумарковские и асимптотические методы, методы регенерирующих процессов и многомерных марковских процессов и т. д.) позволяют оценивать вероятность безотказной работы только для систем с всевозможными допущениями относительно их функционирования и обслуживания. Основными допущениями, как правило, являются экспоненциальность некоторых компонентов или быстрое восстановление элементов системы. В общем случае вычисление системы при произвольных распределениях времени безотказной работы и восстановления элементов сопряжено с большими вычислительными трудностями. Тем не менее, существует всеобъемлющий метод статистического моделирования, который, в принципе, позволяет решать перечисленные и другие аналогичные задачи. Метод, несмотря на его универсальность, имеет существенные недостатки: большое время решения задачи, сложность оценки погрешностей расчетов, отсутствие явных выражений показателей надежности. Однако в некоторых случаях он вполне может использоваться.

Метод статистических испытаний (Монте-Карло) базируется на использовании знаний случайных величин с заданным распределением вероятностей. Сущность метода статистического моделирования состоит в построении алгоритма, имитирующего поведение системы, и реализации этого алгоритма на ЭВМ. В результате статистического моделирования системы получается серия частных значений искомых показателей надежности. Эти значения обрабатываются и классифицируются методами математической статистики, что позволяет получить сведения о надежности реальной системы в произвольные моменты времени. Если количество реализаций достаточно велико, то результаты моделирования системы приобретают статистическую устойчивость и могут быть приняты в качестве оценок искомых показателей надежности.

Теоретической основой метода статистического моделирования на ЭВМ являются предельные теоремы теории вероятностей. Принципиальное значение предельных теорем состоит в том, что они гарантируют высокое качество статистических оценок показателей надежностей при весьма большом числе испытаний (реализаций). Практически приемлемые количественные оценки показателей надежности систем могут быть получены уже при сравнительно небольших значениях .

Предположим, что требуется вычислить неизвестную величину . Это может быть, например, математическое ожидание некоторой случайной величины , т. е. . Пусть при этом среднее квадратическое отклонение случайной величины равно .

Рассмотрим независимых случайных величин , распределения которых совпадают с распределением . Если достаточно велико, то, согласно центральной предельной теореме, распределение величины будет приблизительно нормальным с параметрами и . При этом имеет место приближенное равенство:

(1.1)

где – функция Лапласа.

Это чрезвычайно важное для метода Монте-Карло соотношение. Оно дает нам и метод расчета , и оценку погрешности. В самом деле, из ( 1 .1) видно, что среднее арифметическое значений случайной величины будет приближенно равно . С большой вероятностью ошибка такого приближения не превосходит величины . Очевидно, эта ошибка стремится к нулю с ростом . Уже при числе реализаций это равенство дает хорошее приближение.

Если доверительная вероятность 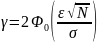, то для обеспечения точности количество испытаний должно быть равно величине . Так, например, при имеем . Конечно, зависит от среднего квадратического отклонения случайной величины , которое иногда заменяется соответствующим выборочным значением.