4.2. Расчет процессов при наддуве топливного бака с использованием газового редуктора

4.2.1. Расчет истечения газа из аккумулятора давления через газовый редуктор

Давление газа в баке по мере расходования компонента поддерживается в указанных пределах за счет подачи газа из системы наддува. Расход газа, поступающего в топливный бак из системы наддува, регулируется:

1) регулятором расхода с постоянной площадью проходного сечения (дроссельная шайба);

2) регулятором расхода с переменной площадью проходного сечения (газовым редуктором).

Первый способ конструктивно прост, но давление наддува в этом случае меняется в довольно широких пределах (прил. 4, рис. 6). Это вынуждает устанавливать в магистрали наддува, например, параллельно несколько шайб, подключенных для подачи газа в бак в процессе работы системы в определенной последовательности. Подключение дополнительной дроссельной шайбы увеличивает расход газа на наддув бака и тем самым давление газа в нем. Во втором способе регулятор может либо обеспечивать постоянство давления газа в баке, либо изменять его по заданной программе.

Использование высокопрочных материалов для изготовления обечайки бака, оптимизация конструкции топливных отсеков и некоторые другие факторы приводят к существенному сужению диапазона допускаемых пределов изменения давления наддува баков. Это вызывает потребность введения в систему наддува особых устройств, регулирующих давление в газовой подушке бака. Такие регуляторы, реагируя, например, на колебания давления в газовой подушке бака, будут изменять площадь проходного сечения специального регулирующего органа, изменяя тем самым количество газа, подаваемого на наддув бака.

Пункты 1–5 и 8 расчета (раздел 4.1) повторять не будем, так как исходные данные не изменились. Полученные значения используем для дальнейшего расчета. В случае коррекции исходных данных (например, при ужесточении требований по диапазону допустимых отклонений давления в баке) их необходимо повторить в полном объеме заново.

Вследствие того, что дроссельная шайба теперь заменена на газовый редуктор, пункты 6 и 7 (о выборе диаметра дросселя и расчете потребного расхода через дроссель) теряют смысл.

23. Определяем значения температуры, плотности, давления газа в аккумуляторе в зависимости от времени работы двигателя при истечении через газовый редуктор.

Законы изменения температуры, плотности и давления в аккумуляторе при опорожнении через газовый редуктор при линейном законе изменения свободного объема газовой подушки , где – скорость изменения объема газовой подушки, равная :

– при адиабатном законе

[Па]; [кг/м³]; [K];

где и ;

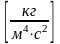– при изотермическом законе

; ; .

Результаты расчетов заносим в таблицу (табл. 3).

24. Строим графики зависимостей давления, плотности, температуры газа в аккумуляторе давления от времени работы двигателя при истечении через газовый редуктор (см. приложение 5).

4.2.2. Расчет геометрических параметров газового редуктора

25. Расчет площади открытия клапана редуктора в зависимости от времени работы двигателя.

Потребный расход газа наддува

[кг/с], где ;

здесь  – коэффициент расхода клапана газового редуктора, примем  = 0,81; f_кл – площадь проходного сечения в газовом редукторе, м².

Выразим площадь клапана из предыдущего уравнения:

.

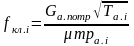Результаты расчетов площади заносим в таблицу (табл. 3).

26. Определение максимальных высоты подъема и площади проходного сечения клапана.

Максимальная площадь клапана будет в конце работы ( = _кон , f_кл.кон = f_кл.max), в момент, когда высота подъема будет максимальной (z_кл.кон= z_кл.max).

Для тарельчатого клапана это значение можно определить следующим образом (см. рис. 6). Площадь проходного сечения клапана

,

где z – высота подъема клапана, м.

Максимальная площадь проходного сечения клапана при z = z_max будет равна площади отверстия

.

С учетом последних двух выражений

.

Таким образом, максимальная высота подъема тарельчатого клапана будет

.

Для конического клапана максимальное значение высоты подъема клапана можно принять

.

Таким образом,

.

27. Определяем диаметр клапана:

,

где f_кл.кон = f_кл.max – площадь проходного сечения клапана в конце работы двигателя (из табл. 3). Округляем до целого полученное значение в миллиметрах.

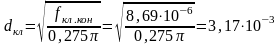м.

Принимаем d_кл=310^-3 м.

28. Определяем высоту подъема клапана в зависимости от времени работы двигателя:

.

Результаты расчетов заносим в таблицу (табл. 3).

29. Строим зависимости площади открытия клапана и высоты подъема клапана от времени работы (см. приложение 5).

Таблица 3

Расчет параметров состояния газа в аккумуляторе давления

при истечении через газовый редуктор

c = 8,37310⁶ , D = 0,33110⁶ , d_кл = 3 мм

, с	0	10	20	30	40	50	60	70	80	90	100
рa, МПа	35,00	32,63	30,27	27,90	25,53	23,16	20,80	18,43	16,06	13,69	11,33
a, кг/м3	409,3	381,6	353,9	326,3	298,6	270,9	243,2	215,5	187,8	160,1	132,5
Тa, K	288	288	288	288	288	288	288	288	288	288	288
fкл , мм2	2,81	3,02	3,25	3,53	3,85	4,25	4,73	5,34	6,13	7,19	8,69
z, мм	0,30	0,32	0,35	0,37	0,41	0,45	0,50	0,57	0,65	0,76	0,92
рп, МПа	0,42	0,51	0,59	0,67	0,73	0,77	0,80	0,79	0,75	0,64	0,42

30. Составим баланс сил, действующих на подвижную систему редуктора с компенсирующей мембраной (рис. 7):

где с₁ – жесткость пружины мембраны; с₂ – жесткость пружины клапана; z_i – высота подъема клапана в любой момент времени; l_зат.1 и l_зат.2 – начальная затяжка соответствующих пружин; p_п – давление газа на выходе из редуктора (давление подачи); F_кл – площадь поверхности клапана, на которую действует давление газа; p₀ – давление окружающей среды; p_а.i – давление газа на входе в редуктор (в газовом аккумуляторе) в любой момент времени; F_м.эф.1 и F_м.эф.2 – эффективные площади соответствующих мембран (основной 1 и компенсирующей 2).

Находим величину давления на выходе из редуктора:

.

Представив это выражение в виде ряда слагаемых, получим

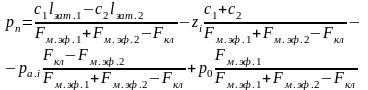(59)

Из уравнения (59) видно, что первый и четвертый члены постоянны и не зависят от условий работы редуктора. Второй член зависит от величины подъема клапана, а третий – от двух величин: давления газа на входе в редуктор и разности площадей клапана и эффективной площади второй мембраны. Поэтому величина третьего слагаемого может легко изменяться по желанию конструктора.

31. Площадь второй мембраны выбирают исходя из следующих соображений. Поскольку закон изменения величин второго и третьего членов разный, то получить их сумму постоянной в соответствии с выражением (59) на всем диапазоне давлений на входе в редуктор не представляется возможным. Но задавшись равенством давления на выходе из редуктора для двух любых точек характеристики (обычно это делают для начала и конца работы двигательной установки, т.е. ), можно получить следующее соотношение:

,

из которого легко определить необходимый размер второй мембраны:

.

В этом случае, как и для основной мембраны, площадь F_м.эф.2 является эффективной, а ее геометрические размеры рассчитываются в соответствии с выражением

,

где F_м.2, D₂, D_м.2 – геометрическая площадь, диаметр жесткого днища и наружный диаметр компенсирующей мембраны соответственно:

; .

Определяем площадь поверхности клапана:

м².

Начальные и конечные значения давления газа в аккумуляторе и высоты подъема клапана выбираем из таблицы 3:

p_а.нач = 35,0010⁶ Па, p_а.кон = 11,3310⁶ Па,

z_нач = 0,3010^-3 м, z_кон = 0,9210^-3 м.

32. Выбираем пружины и производим их расчет (по ГОСТ 13765-86) [1].

Пружина клапана

Выбираем винтовую цилиндрическую пружину сжатия 110 по ГОСТ 13767-86 (класс I, разряд 2) со следующими параметрами:

– сила F₃ пружины при максимальной деформации – 5 Н;

– диаметр проволоки d – 0,4 мм;

– наружный диаметр пружины D₁ = 3 мм;

– жесткость с₁^' одного витка – 14,290 Н/мм;

– наибольший прогиб одного витка s₃^' – 0,351 мм.

Назначаем число витков пружины: n = 3.

Полное число витков: n₁ = n + n₂ = 3 + 1,5 = 4,5,

где n₂ – число нерабочих витков.

Жесткость пружины: с = с₁^' / n = 14,290 / 3 = 4,763 Н/мм = 4763 Н/м.

Средний диаметр пружины: D = D₁ – d = 3 – 0,4 = 2,6 мм.

Рабочая деформация пружины (соответствует наибольшему принудительному перемещению подвижного звена в механизме) s₂: для нашего газового редуктора наибольшее перемещение соответствует максимальной высоте подъема клапана, которую выбираем из таблицы 3,

s₂ = z_кон = 0,92 мм.

Сила пружины при рабочей деформации: F₂ = cs₂ = 4,7630,92 = 4,382 Н.

Сила пружины при максимальной деформации:

,

где  – относительный инерционный зазор пружины сжатия (для пружин классов I и II  = 0,05…0,25).

Н.

Значение силы при максимальной деформации выбранной пружины F₃ = 5 Н попадает в полученный интервал, значит пружина выбрана правильно.

Максимальная деформация пружины: s₃ = F₃ / c = 5 / 4,763 = 1,05 мм.

Длина пружины при максимальной деформации:

l₃ = (n₁ + 1 – n₃)d = (4,5 + 1 – 1,5)0,4 = 1,60 мм,

где n₃ – число обработанных витков.

Длина пружины в свободном состоянии: l₀ = l₃ + s₃ = 1,60 + 1,05 = 2,65 мм.

Длина пружины при рабочей деформации: l₂ = l₀ – s₂ = 2,65 – 0,92 = 1,73 мм.

Пружина мембраны

По аналогичной методике подбираем пружину для мембраны:

винтовая цилиндрическая пружина сжатия 186 по ГОСТ 13767-86 (класс I, разряд 2) со следующими параметрами:

– сила F₃ пружины при максимальной деформации – 12,5 Н;

– диаметр проволоки d – 0,6 мм;

– наружный диаметр пружины D₁ – 4 мм;

– жесткость с₁^' одного витка – 32,310 Н/мм;

– наибольший прогиб одного витка s₃^' – 0,387 мм.

Число витков пружины: n = 3.

Полное число витков: n₁ = 4,5.

Жесткость пружины: с = 10,77 Н/мм = 10770 Н/м.

Средний диаметр пружины: D = 3,4 мм.

Рабочая деформация пружины: s₂ = 0,92 мм.

Сила пружины при рабочей деформации: F₂ = 9,908 Н.

Сила пружины при максимальной деформации: Н.

Максимальная деформация пружины: s₃ = 1,16 мм.

Длина пружины при максимальной деформации: l₃ = 2,40 мм.

Длина пружины в свободном состоянии: l₀ = 3,56 мм.

Длина пружины при рабочей деформации: l₂ = 2,64 мм.

33. Определяем эффективную площадь компенсирующей мембраны:

где с₁ = 10770 Н/м – жесткость пружины мембраны; где с₂ = 4763 Н/м – жесткость пружины клапана.

34. Находим геометрические размеры компенсирующей мембраны 2:

– наружный диаметр компенсирующей мембраны

м;

– диаметр жесткого днища

м.

Анализируя геометрические размеры пружин, клапана и компенсирующей мембраны можно сделать вывод, что пружины могут быть установлены в габаритах клапана и мембраны.

35. Определяем геометрические размеры основной мембраны 1.

Задаемся наружным диаметром мембраны D_м.1 = 3,5 мм = 3,510^-3 м.

Диаметр жесткого днища мембраны 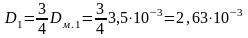м.

Геометрическая площадь мембраны

м².

Эффективная площадь основной мембраны

м².

36. Находим начальные затяжки пружины 1 мембраны l_зат.1 и пружины 2 клапана l_зат.2.

Из выражения (59) получим:

.

Задаемся начальной затяжкой пружины 2 клапана l_зат.2 = 0,510^-3 м.

Давление окружающей среды принимаем нормальным атмосферным:

р₀ = 101325 Па.

Остальные параметры выбираем соответствующими началу работы двигательной установки: р_п.нач = р_ном = 0,42 МПа; z_нач = 0,310^-3 м; p_а.нач = 3510⁶ Па.

Тогда начальная затяжка пружины 1 мембраны:

.

37. Определяем значения давления газа наддува в подушке бака в зависимости от времени работы двигателя при истечении через газовый редуктор по выражению (59):

.

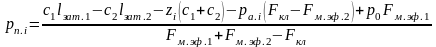Результаты расчетов заносим в таблицу (табл. 3).

38. Строим график зависимости давления газа наддува в подушке бака от времени работы двигателя при истечении через газовый редуктор (прил. 5).