
- •Расчет процессов в аккумуляторе давления и газовой подушке бака
- •1. Основные положения
- •1.1. Цель и задачи расчетно-графической работы
- •1.2. Содержание расчетно-графической работы и требования к ней
- •2. Рекомендации по выполнению основной части расчетно-пояснительной записки
- •2.1. Процессы в топливных баках ракет при их наддуве
- •2.2. Основные уравнения термодинамического тела переменной массы
- •2.3. Расход газа при истечении
- •2.4. Опорожнение емкости через отверстие постоянной площади
- •2.5. Опорожнение емкости через газовый редуктор
- •2.6. Наполнение емкости постоянного объема
- •2.7. Наполнение емкости переменного объема
- •3. Цель и задачи расчета, исходные данные
- •4. Пример расчета процессов в аккумуляторе давления и газовой подушке бака
- •4.1. Расчет процессов в аккумуляторе давления и газовой подушке бака при использовании дроссельной шайбы
- •4.1.1. Расчет истечения газа из аккумулятора давления через дроссель постоянного проходного сечения
- •4.1.2. Расчет процессов в газовой подушке бака при использовании дроссельной шайбы
- •4.2. Расчет процессов при наддуве топливного бака с использованием газового редуктора
- •4.2.1. Расчет истечения газа из аккумулятора давления через газовый редуктор
- •4.2.2. Расчет геометрических параметров газового редуктора
- •Вопросы для самоконтроля
- •Библиографический список
- •Приложения
- •Приложение 3
2.2. Основные уравнения термодинамического тела переменной массы
Основной особенностью термодинамических процессов, происходящих при наддуве топливного бака, является изменение энергии, которое вызывается изменением массы рабочего тела. При исследовании процессов с переменным количеством газа существенное значение имеет зависимость, представляющая собой закон изменения состояния переменного количества газа:
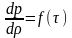 ,
,
где p, – давление и плотность газа соответственно; – время.
Из последнего уравнения видно, что в процессах с переменным количеством газа для однозначного определения состояния газа необходимо иметь значения не двух параметров, как в случае процессов с постоянным количеством газа, а трех, при этом дополнительным параметром является время . Остальные величины, входящие в приведенное уравнение, являются функциями времени.
При известных значениях давления p = p() и плотности = () в емкости, температуру T() можно найти из уравнения состояния
 ,
(1)
,
(1)
где R0 – удельная газовая постоянная.
При выводе первого закона термодинамики для переменной массы рабочего тела воспользуемся физической моделью системы наддува емкости (рис. 1).
В процессе наддува параметры газа в емкости изменяются во времени. Кроме того, изменяется масса газа внутри емкости как в результате физических процессов испарения и конденсации, так и в результате протекания химических реакций между газом наддува и жидкостью, а также сброса газа через дренажный клапан. Таким образом, процесс наддува протекает с переменным количеством газа в емкости.
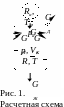 Рассмотрим
расчетную схему для определения
параметров системы наддува (рис. 1). В
момент времени
= 0 начинается
наддув емкости газом из газогенератора,
состав которого, как и давление pa
и температура Ta,
известны. Рассмотрим теперь энергетический
баланс газа наддува, заключенного
в
свободном пространстве емкости. Обозначим
через Gа,
GИ,
GК,
GД
массовые расходы газа, поступающего в
емкость; испаряющейся жидкости;
конденсата, выпадающего из рабочего
тела наддува внутри емкости; газа,
удаляющегося через дренажный клапан
из емкости.
Рассмотрим
расчетную схему для определения
параметров системы наддува (рис. 1). В
момент времени
= 0 начинается
наддув емкости газом из газогенератора,
состав которого, как и давление pa
и температура Ta,
известны. Рассмотрим теперь энергетический
баланс газа наддува, заключенного
в
свободном пространстве емкости. Обозначим
через Gа,
GИ,
GК,
GД
массовые расходы газа, поступающего в
емкость; испаряющейся жидкости;
конденсата, выпадающего из рабочего
тела наддува внутри емкости; газа,
удаляющегося через дренажный клапан
из емкости.
Пусть а – удельный приток энергии с поступающим в емкость газом; iИ, iК и iД – энтальпии паров компонента, конденсата и газа, удаляющегося из емкости через дренажный клапан.
Обозначим: dQW, dQЖ – потери теплоты в результате теплообмена между стенками емкости и поверхностью жидкости соответственно; dQХ – тепловой эффект химических реакций и физико-химических превращений на границе раздела; dU – изменение удельной внутренней энергии газа в емкости; pdV – работа вытеснения жидкости из емкости; аGad – приход энергии в емкость в связи с притоком массы газа Gadτ; iИGИd – приход энергии в емкость с испаряющейся массой жидкости GИdτ; iДGДd – уход энергии из емкости с массой газа GДd через дренажный клапан; iКGКd – уход энергии из емкости в связи с выпадением в конденсат массы газа GКd.
В соответствии с уравнением баланса энергии для газа, заключенного в свободном объеме бака, имеем

или
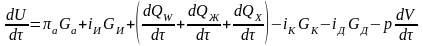 . (2)
. (2)
Удельный приток энергии с поступающим газом можно выразить следующим образом:
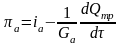 , (3)
, (3)
где iа – энтальпия газа на выходе из газогенератора (аккумулятора); dQтр – секундная потеря энергии на теплоотдачу в газоподводящем канале.
Состав газа внутри емкости изменяется в результате химических реакций в самом рабочем теле, а также в результате тепло- и массообмена между жидкостью и газом наддува.
Дифференцируя по времени выражение для внутренней удельной энергии

и учитывая, что
 ,
,
находим
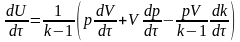 .
(4)
.
(4)
После подстановки в уравнение (2) выражения (3) имеем
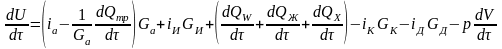 .
(5)
.
(5)
Полученное уравнение представляет собой аналитическое выражение первого закона термодинамики применительно к тепловым процессам, протекающим с переменным количеством газа, и называется энергетическим уравнением переменного количества рабочего тела.
Из последнего уравнения с учетом выражения (4) легко получить после преобразования так называемое уравнение скорости изменения давления газа:
 .
(6)
.
(6)
Для изменения количества газа в свободном объеме емкости за время d можно записать закон сохранения массы в следующем виде:
 ,
,
откуда получаем уравнение изменения количества газа
 . (7)
. (7)
Найдем
теперь зависимость
,
которая имеет существенное значение
при исследовании характера процесса с
переменным количеством газа. Дифференцируя
выражение
 с учетом уравнения (7), находим
с учетом уравнения (7), находим
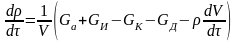 , (8)
, (8)
откуда,
используя выражение (6) для
 ,
получаем уравнение
изменения состояния переменного
количества газа
,
получаем уравнение
изменения состояния переменного
количества газа
 .
(9)
.
(9)
Выражения (6)–(9) совместно с уравнением состояния (1) составляют систему уравнений однозначно описывающих термодинамическое тело переменной массы.
Из полученной системы можно найти уравнения при следующих допущениях:
1) потеря теплоты в единицу времени в газоподводящем канале пренебрежимо мала, т.е.
 ;
;
2) состав газа внутри емкости не изменяется, т.е.
 и
и  ;
;
3) количество конденсата и испаряющейся жидкости пренебрежимо мало, т.е.
 и
и  .
.
Система уравнений (6)–(9) при этих допущениях выглядят следующим образом:
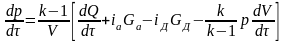 ;
(10)
;
(10)
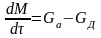 ; (11)
; (11)
 ; (12)
; (12)
 . (13)
. (13)
Уравнения (10)–(13) в дальнейшем будут использоваться для определения параметров газа в емкости при ее опорожнении и наполнении.
