-15.2 16. Оптимальное распределение нагрузки между агрегатами электростанций. Оптимальная последовательность включения

агрегатов электростанций

где , – относительные приросты расхода тепла при изменении величины отбора и постоянстве электрической мощ­ности; – относительный прирост расхода тепла при изменении электрической мощности.

Распределение нагрузки между агрегатами ГЭС. Для ГЭС наивыгоднейшее распределе­ние нагрузки будет в том случае, когда агрегаты рабо­тают с равными относительными приростами:

Из условий наивыгоднейшего распределения нагрузки следует, что методика решения задачи о наивыгоднейшем распреде­лении нагрузки между агрегатами электростанций проста, если известны их характеристики относительных приростов.

В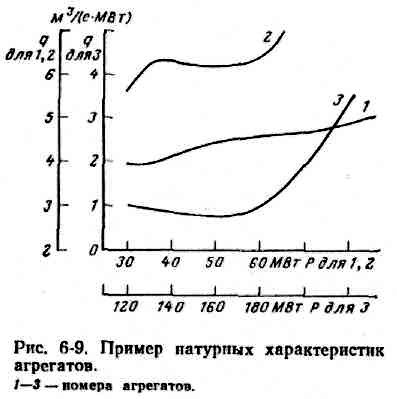 условиях эксплуатации желательно было бы при распределении нагрузки между агрегатами использовать не характеристики, а текущие измерения относительных приростов. Для ГЭС, чтобы получить относительный прирост агрегата, нужно измерить расходы Q₁ и Q₂ и мощности Р₁ и Р₂ с малым шагом дискретности, т. е. получить

Этот дифференциальный показатель очень чувствителен к погрешностям измерения расходов и мощностей, может резко меняться, поэтому измеренные характеристики относительных приростов обычно не являются выпуклыми, не удовле­творяют требованиям метода неопределенных множите­лей Лагранжа и точность их низка.

На рис. 6-9 показаны характеристики относительных приростов различных гидроагрегатов, полу­ченные при натурных испытаниях. Прежде чем воспользоваться такими характеристиками, нужно их обработать. Некачественность хар-к приво­дит к снижению эффекта оптимального распределения нагрузки между агрегатами.

17. 18. Оптимизация режима с учетом потерь активной мощности при передаче. Метод линейных коэффициентов токораспред-я.

Один из возможных м-дов, примен-х для определения потерь активной мощ-ти при передаче эл/энергии, явл. м-д линейных коэф-в токорас-я.

Суть данного м-да заключается в следующем: ток каждой ветви сети в рассмат-м режиме м. б. получен как сумма токов частных режимов, в каждом из кот-х генерация и нагрузка присутствуют только в одном из независимых узлов. Таким образом, число таких частных режимов равно п - числу независимых узлов. Коэф-т токораспределения α_ij (где i-номер ветви, j – номер узла)

В соответствии с методом наложения ток каждой ветвей I_ni есть сумма токов протекающих по этой ветви во всех частных режимах:

При равенстве всех узловых напряжений, для j=1..n+1, где n+1-число узлов, комплексная мощность S_лi протекающая по i-й линии

Тогда потери при передаче мощн по i-й линии составят:

в том числе активная составляющая потерь

и суммарные по энергосистеме потери активной мощности при передаче, МВт

Знание зависимости позволяет определить относительные приросты суммарных потерь передаваемой мощности при изменении мощности какой либо электростанции , где s=1,2..n-

номер эл/ст., и условие оптимального распределения активной мощности м/у эл/ст. с учётом потерь