Практикум по эконометрике разработан в Новгородском Государственном Университете на кафедре прикладной математики, май 2002 г.

Авторы:

• Беляева А.А.

• Савина Т.А.

• Смолина А.П.

    Практикум по эконометрике представляет собой учебное пособие, призванное предоставить в распоряжение студентов экономических специальностей достаточно простое и доступное руководство по изучению основ эконометрики. Изложение каждой темы сопровождается экспериментами по методу Монте-Карло, иллюстрирующими проблемы, изучаемые в курсе эконометрики и в заключение каждой темы предлагается тест для самопроверки.

Содержание

Свойства коэффициентов регрессии

• Случайные составляющие коэффициентов регрессии

• Эксперимент по методу Монте-Карло

• Предположения о случайном члене

• Несмещенность коэффициентов регрессии

• Точность коэффициентов регрессии

• Теорема Гаусса-Маркова

Последствия неправильной спецификации модели

• Введение

• Влияние невключения значимой переменной

• Влияние включения в модель "лишней" переменной

Гетероскедастичность

• Введение

• Гомоскедастичность и гетероскедастичность

• Влияние гетероскедастичности на оценивание

• Обнаружение гетероскедастичности

• Коррекция модели при гетероскедастичности

Автокорреляция

• Причины возникновения автокорреляции

• Проблема автокорреляции

• Обнаружение автокорреляции первого порядка: критерий Дарбина-Уотсона

• Исправление автокорреляции

• Методы оценивания коэффициента автокорреляции

• Автокорреляция как следствие неправильной спецификации модели

• Автокорреляция в модели с лаговой зависимой переменной

• Самостоятельная работа

Приложения

• Приложение 1.1

• Приложение 1.2

• Приложение 2.1

• Приложение 2.2

• Приложение 3.1

Свойства коэффициентов регрессии

Случайные составляющие коэффициентов регрессии

 Коэффициенты регрессии, вычисленные методом наименьших квадратов- это особая форма случайной величины , свойства которой зависят от свойств остаточного члена в уравнении. Мы продемонстрируем это сначала теоретически, а потом посредством контролируемого эксперимента. В частности, мы увидим, какое значение для оценки имеют предположения относительно характера остаточного члена.

      В ходе рассмотрения мы будем постоянно иметь дело с моделью парной регрессии, в которой y связан с x следующей зависимостью:

      

      и на основе N выборочных наблюдений будем оценивать уравнение регрессии:

      

      Будем также предполагать, что x-неслучайная экзогенная переменная, а случайная эндогенная переменная y включает неслучайную составляющую, которая не имеет ничего общего с законами вероятности ( a и b могут быть неизвестными, но тем не менее это постоянные величины), и случайную составляющую и. Отсюда следует, что, когда мы вычисляем b по обычной формуле: (1.3)

      

       b также содержит случайную составляющую. Cov (x, у) зависит от значений у, а у зависит от значений u.

      Если случайная составляющая принимает разные значения в N наблюдениях, то мы получаем различные значения у и, следовательно, разные величины Cov (x, у) и b.

      Теоретически мы можем разложить b на случайную и неслучайную составляющие. Воспользовавшись соотношением (1.1), а также свойством ковариации, получим:

      

      По свойствам ковариации равна нулю, а ковариация равна . Причем Cov(х, х) это тоже, что и Var(x). Следовательно, мы можем записать:

      

      и, таким образом,

      

      Итак, мы показали, что коэффициент регрессии b, полученный по любой выборке, представляется в виде суммы двух слагаемых: 1) постоянной величины, равной истинному значению коэффициента ; 2) случайной составляющей, зависящей от Cov (x, u), которой обусловлены отклонения коэффициента b от константы .

      Аналогичным образом можно показать, что а имеет постоянную составляющую, равную истинному значению , плюс случайную составляющую, которая зависит от случайного фактора u.

      Следует заметить, что на практике мы не можем разложить коэффициенты регрессии на составляющие, так как не знаем истинных значений или фактических значений и в выборке. Они интересуют нас потому, что при определенных предположениях позволяют получить некоторую информацию о теоретических свойствах а и Ь.

Эксперимент по методу Монте-Карло

Проблема состоит в том, что мы никогда не знаем истинных значений (иначе зачем бы мы использовали регрессионный анализ для их оценки?). Поэтому мы не можем сказать, хорошие или плохие оценки дает наш метод.

       Эксперимент по методу Монте-Карло — это искусственный контролируемый эксперимент, дающий возможность такой проверки. Простейший возможный эксперимент по методу Монте-Карло состоит из трех частей.

      Во-первых: 1) выбираются истинные значения ; 2) в каждом наблюдении выбирается детерминированное значение x; 3) используется некоторый процесс генерации случайных чисел (или берется последовательность из таблицы случайных чисел) для получения значений случайного фактора и в каждом из наблюдений.

      Во-вторых, в каждом наблюдении генерируется значение y с использованием соотношения (1.1) и значений , x и u.

      В-третьих, применяется регрессионный анализ для оценивания параметров а и Ь с использованием только полученных указанным образом значений у и данных для x.

      При этом вы можете видеть, являются ли a и b хорошими оценками , и это позволит почувствовать пригодность метода построения регрессии.

      На первых двух шагах проводится подготовка к применению регрессионного метода. Мы полностью контролируем модель, которую создаем, и знаем истинные значения параметров , потому что сами их определили. На третьем этапе мы определяем, может ли поставленная нами задача решаться с помощью метода регрессии, т. е. могут ли быть получены хорошие оценки для при использовании только данных об у и x.

      Заметим, что проблема возникает вследствие включения случайного фактора в процесс получения у. Если бы этот фактор отсутствовал, то точки, соответствующие значениям каждого наблюдения, лежали бы точно на прямой (1.1) и точные значения можно было бы очень просто определить по значениям у и x.

      Поясним суть метода на примере:

      Произвольно положим , так что истинная зависимость имеет вид:

      

      Предположим для простоты, что имеется 20 наблюдений и что х принимает значения от 1 до 20. Случайный член и нормально распределен с нулевым мат. ожиданием и единичной дисперсией. Нам потребуется набор из 20 значений, обозначим их . Случайный член u в первом наблюдении просто равен , и т. д.

      Зная значения х и и в каждом наблюдении, можно вычислить значения у, используя уравнение (1.7); это сделано в табл. 1.1.

      

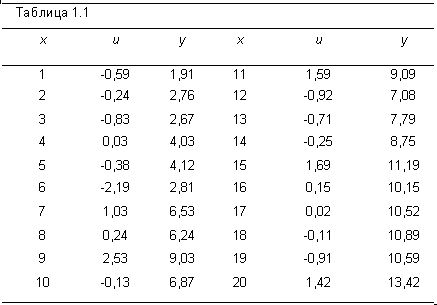
       Теперь при оценивании регрессионной зависимости у от х получим:

      

      В данном случае оценка а приняла меньшее значение (1,63) по сравнению с (2,00), a b немного выше (0,54 по сравнению с 0,50). Расхождения вызваны совместным влиянием случайных членов в 20 наблюдениях.

      Очевидно, что одного эксперимента такого типа едва ли достаточно для оценки качества метода регрессии. Он дал довольно хорошие результаты, но, возможно, это лишь счастливый случай. Для дальнейшей проверки повторим эксперимент с тем же истинным уравнением (1.7) и с теми же значениями х, но с новым набором случайных чисел для остаточного члена, взятых из того же распределения (нулевое среднее и единичная дисперсия). Используя эти значения и значения х, получим новый набор значений у.

      В целях экономии места таблица с новыми значениями и и у не приводится. Вот результат оценивания регрессии между новыми значениями у и х:

      

      Второй эксперимент также был успешным. Теперь а оказалось больше , a b — несколько меньше . В табл. 1.2 приведены оценки a и b при 10-кратном повторении эксперимента с использованием разных наборов случайных чисел в каждом варианте.

      

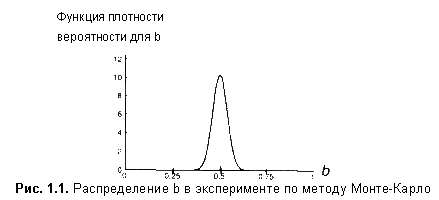
      Можно заметить, что, несмотря на то что в одних случаях оценки принимают заниженные значения, а в других — завышенные, в целом значения a и b группируются вокруг истинных значений , равных соответственно 2,00 и 0,50. При этом хороших оценок получено больше, чем плохих. Например, фиксируя значения b при очень большом числе повторений эксперимента, можно построить таблицу частот и получить аппроксимацию функции плотности вероятности, показанную на рис. 1.1. Это нормальное распределение со средним 0,50 и стандартным отклонением 0,0388.

      

      Выше говорилось, что расхождения между коэффициентами регрессии и истинными значениями параметров вызваны случайным членом и. Отсюда следует, что чем больше элемент случайности, тем, вообще говоря, менее точными являются оценки.

      Этот вывод будет проиллюстрирован с помощью второй серии экспериментов по методу Монте-Карло, связанной с первой. Мы будем использовать те же значения , что и раньше, те же значения х и тот же источник случайных чисел для генерирования случайного члена, но теперь будем брать удвоенные значения случайного члена в каждом наблюдении. Выразим через , значения случайного члена, которые равны удвоенному случайному числу: . Фактически мы используем в точности ту же выборку случайных чисел, что и раньше, но на этот раз удвоим их значения. Теперь на основе данных табл. 1.1 рассчитаем табл. 1.3. Далее, оценивая регрессию между у и х, получим уравнение:

      

      Это уравнение гораздо менее точно, чем уравнение (1.8). В табл. 1.4 приведены результаты всех 10 экспериментов при u'= 2rn.

      

      Мы будем называть это серией экспериментов II, а первоначальную серию экспериментов, результаты которых приведены в табл. 1.2, — серией I. При сравнении табл. 1.2 и 1.4 можно видеть, что значения а и b во второй таблице являются значительно более неустойчивыми, хотя в них по-прежнему нет систематической тенденции к занижению или завышению значений оценок. Детальное исследование позволяет обнаружить важную особенность. В серии I значение b в эксперименте 7 было равно 0,54, и завышение оценки составило 0,04. В серии II значение b в эксперименте 7 равнялось 0,58 и завышение составило 0,08, т. е. оно было ровно вдвое больше, чем раньше. То же самое повторяется для каждого из 9 других экспериментов, а также для коэффициента регрессии а в каждом эксперименте. Удвоение случайного члена в каждом наблюдении приводит к удвоению ошибок в значениях коэффициентов регрессии.

      Этот результат следует непосредственно из разложения b в соответствии с уравнением (1.6). В серии I случайная ошибка в b задается в виде . В серии II она представлена как , и

      

      Увеличение неточности отражено в функции плотности вероятности для b в серии II, показанной на рис. 1.2.

      

      Эта функция вновь симметрична относительно истинного значения 0,50, однако если вы сравните ее с функцией, изображенной на рис. 1.1, то увидите, что данная кривая более полога и широка. Удвоение значений и привело к удвоению стандартного отклонения распределения.

Предположения о случайном члене

 Итак, очевидно, что свойства коэффициентов регрессии существенным образом зависят от свойств случайной составляющей. В самом деле, для того чтобы регрессионный анализ, основанный на обычном методе наименьших квадратов, давал наилучшие из всех возможных результаты, случайный член должен удовлетворять четырем условиям, известным как условия Гаусса—Маркова. Не будет преувеличением сказать, что именно понимание важности этих условий отличает компетентного исследователя, использующего регрессионый анализ, от некомпетентного. Если эти условия не выполнены, исследователь должен это сознавать. Если корректирующие действия возможны, то аналитик должен быть в состоянии их выполнить. Если ситуацию исправить невозможно, исследователь должен быть способен оценить, насколько серьезно это может повлиять на результаты.

      Рассмотрим теперь эти условия одно за другим, объясняя кратко, почему они имеют важное значение. Три последних условия будут также подробно рассмотрены в следующих главах.

      

      Первое условие состоит в том, что математическое ожидание случайного члена в любом наблюдении должно быть равно нулю. Иногда случайный член будет положительным, иногда отрицательным, но он не должен иметь систематического смещения ни в одном из двух возможных направлений.

      Фактически если уравнение регрессии включает постоянный член, то обычно бывает разумно предположить, что это условие выполняется автоматически, так как роль константы состоит в определении любой систематической тенденции в у, которую не учитывают объясняющие переменные, включенные в уравнение регрессии.

      

      Второе условие состоит в том, что дисперсия случайного члена должна быть постоянна для всех наблюдений. Иногда случайный член будет больше, иногда меньше, однако не должно быть априорной причины для того, чтобы он порождал большую ошибку в одних наблюдениях, чем в других.

      Эта постоянная дисперсия обычно обозначается , или часто в более краткой форме , а условие записывается следующим образом:

      

      

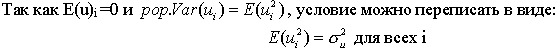
      Величина , конечно, неизвестна. Одна из задач регрессионного анализа состоит в оценке стандартного отклонения случайного члена.

      Если рассматриваемое условие не выполняется, то коэффициенты регрессии, найденные по обычному методу наименьших квадратов, будут неэффективны, и можно получить более надежные результаты путем применения модифицированного метода регрессии. Это будет рассмотрено в главе 3.

      

      Это условие предполагает отсутствие систематической связи между значениями случайного члена в любых двух наблюдениях. Например, если случайный член велик и положителен в одном наблюдении, это не должно обусловливать систематическую тенденцию к тому, что он будет большим и положительным в следующем наблюдении (или большим и отрицательным, или малым и положительным, или малым и отрицательным). Случайные члены должны быть абсолютно независимы друг от друга.

      В силу того, что , данное условие можно записать следующим образом:

      

      Если это условие не будет выполнено, то регрессия, оцененная по обычному методу наименьших квадратов, вновь даст неэффективные результаты. В главе 4 рассматриваются возникающие здесь проблемы и пути их преодоления.

      

      В большинстве глав мы будем в сущности использовать более сильное предположение о том, что объясняющие переменные не являются стохастическими, т. е. не имеют случайной составляющей. Значение любой независимой переменной в каждом наблюдении должно считаться экзогенным, полностью определяемым внешними причинами, не учитываемыми в уравнении регрессии.

      Если это условие выполнено, то теоретическая ковариация между независимой переменной и случайным членом равна нулю. Так как E(u_i)=0, то

      

      Следовательно, данное условие можно записать также в виде:

      

      В главах 3 и 4 рассматриваются два важных случая, в которых данное условие не выполнено, и последствия этого.

      Предположение о нормальности

      Наряду с условиями Гаусса—Маркова обычно также предполагается нормальность распределения случайного члена. Дело в том, что если случайный член и нормально распределен, то так же будут распределены и коэффициенты регрессии. Это условие пригодится, когда потребуется проводить проверку гипотез и определять доверительные интервалы для , используя результаты построения регрессии.

      Предположение о нормальности основывается на центральной предельной теореме. В сущности, теорема утверждает, что если случайная величина является общим результатом взаимодействия большого числа других случайных величин, ни одна из которых не является доминирующей, то она будет иметь приблизительно нормальное распределение, даже если отдельные составляющие не имеют нормального распределения.

      Случайный член u определяется несколькими факторами, которые не входят в явной форме в уравнение регрессии. Поэтому даже если мы ничего не знаем о распределении этих факторов (или даже об их сущности), мы имеем право предположить, что они нормально распределены.

Несмещенность коэффициентов регрессии

 На основании уравнения (1.6) можно показать, что b будет несмещенной оценкой , если выполняется 4-е условие Гаусса—Маркова:

      

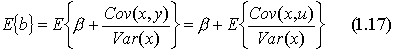
      так как — константа. Если мы примем сильную форму 4-го условия Гаусса-Маркова и предположим, что x— неслучайная величина, мы можем также считать Var (x) известной константой и, таким образом,

      

      Далее, если х — неслучайная величина, то E(Cov(x,u))=0 и, следовательно,

      

      Таким образом, b — несмещенная оценка . Можно получить тот же результат со слабой формой 4-го условия Гаусса—Маркова (которая допускает, что переменная х имеет случайную ошибку, но предполагает, что она распределена независимо от и).

      За исключением того случая, когда случайные факторы в N наблюдениях в точности «гасят» друг друга, что может произойти лишь при случайном совпадении, b будет отличаться от в каждом конкретном эксперименте. Однако с учетом соотношения (1.19) не будет систематической ошибки, завышающей или занижающей оценку. То же самое справедливо и для коэффициента a.

      

      Следовательно,

      

      Поскольку у определяется уравнением (1.1), то

      

      так как E(u_i)=0, если выполнено 1-е условие Гаусса—Маркова. Следовательно,

      

      Подставив это выражение в (1.21) и воспользовавшись тем, что получим:

      

      Таким образом, а — это несмешенная оценка при условии выполнения 1-го и 4-го условий Гаусса—Маркова. Безусловно, для любой конкретной выборки фактор случайности приведет к расхождению оценки и истинного значения.

Точность коэффициентов регрессии

Рассмотрим теперь теоретические дисперсии оценок а и b. Они задаются следующими выражениями (доказательства для эквивалентных выражений можно найти в работе Дж. Томаса [Thomas, 1983, section 8.3.3]):

      

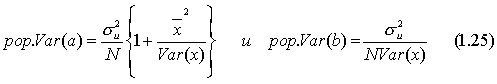
      Из уравнения (1.25) можно сделать три очевидных заключения. Во-первых, дисперсии а и b прямо пропорциональны дисперсии остаточного члена . Чем больше фактор случайности, тем хуже будут оценки при прочих равных условиях. Это уже было проиллюстрировано в экспериментах по методу Монте-Карло в разделе 1.2. Оценки в серии II были гораздо более неточными, чем в серии I, и это произошло потому, что в каждой выборке мы удвоили случайный член. Удвоив u, мы удвоили его стандартное отклонение и, следовательно, удвоили стандартные отклонения а и b. Во-вторых, чем больше число наблюдений, тем меньше дисперсии оценок. Это также имеет определенный смысл. Чем большей информацией вы располагаете, тем более точными, вероятно, будут ваши оценки. В-третьих, чем больше дисперсия х, тем меньше будет дисперсия коэффициентов регрессии. В чем причина этого?

      Напомним, что 1) коэффициенты регрессии вычисляются на основании предположения, что наблюдаемые изменения у происходят вследствие изменений х, но 2) в действительности они лишь отчасти вызваны изменениями х, а отчасти вариациями и.

      Чем меньше дисперсия х, тем больше, вероятно, будет относительное влияние фактора случайности при определении отклонений у и тем более вероятно, что регрессионный анализ может оказаться неверным. В действительности, как видно из уравнения (1.25), важное значение имеет не абсолютная, а относительная величина и Var (х).

      На практике мы не можем вычислить теоретические дисперсии а или b, так как неизвестно, однако мы можем получить оценку на основе остатков. Очевидно, что разброс остатков относительно линии регрессии будет отражать неизвестный разброс и относительно линии , хотя в общем остаток и случайный член в любом данном наблюдении не равны друг другу. Следовательно, выборочная дисперсия остатков Var(e), которую мы можем измерить, сможет быть использована для оценки которую мы получить не можем.

      Прежде чем пойти дальше, задайте себе следующий вопрос: какая прямая будет ближе к точкам, представляющим собой выборку наблюдений по х и у: истинная прямая или линия регрессии ? Ответ будет таков: линия регрессии, потому что по определению она строится таким образом, чтобы свести к минимуму сумму квадратов расстояний между ней и значениями наблюдений. Следовательно, разброс остатков у нее меньше, чем разброс значений и, и Var(e) имеет тенденцию занижать оценку . Действительно, можно показать, что математическое ожидание Var (e), если имеется всего одна независимая переменная, равно . Однако отсюда следует, что если определить как

      

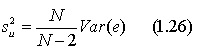
      то будет представлять собой несмещенную оценку (см. доказательство в работе Дж. Томаса).

      Используя уравнения (1.25) и (1.26), можно получить оценки теоретических дисперсий для a и b, и после извлечения квадратного корня — оценки их стандартных отклонений. Вместо слишком громоздкого термина «оценка стандартного отклонения функции плотности вероятности» коэффициента регрессии будем использовать термин «стандартная ошибка» коэффициента регрессии, которую в дальнейшем мы будем обозначать в виде сокращения «с. о.» Таким образом, для парного регрессионного анализа мы имеем:

      

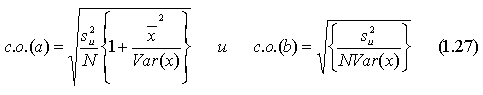
      Полученные соотношения будут проиллюстрированы экспериментами по методу Монте-Карло, описанными в разделе 1.2. В серии I и определялось на основе случайных чисел, взятых из генеральной совокупности с нулевым средним и единичной дисперсией ( = 1), а х представлял собой набор чисел от 1 до 20. Можно легко вычислить Var (х), которая равна 33,25. Следовательно,

      

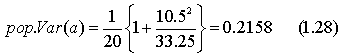
      и

      

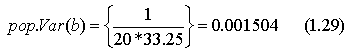
      Таким образом, истинное стандартное отклонение для b равно . В таблице 1.5 представлены результаты вычислений стандартного отклонения на основе 10-ти опытов. Как видите, большинство оценок достаточно хороши.

      

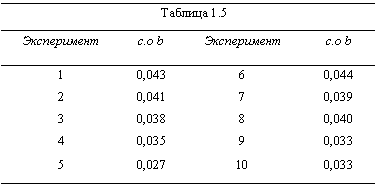
      Следует подчеркнуть один основной момент. Стандартная ошибка дает только общую оценку степени точности коэффициента регрессии. Она позволяет вам получить некоторое представление о кривой функции плотности вероятности, как показано на рис. 1.1. Однако она не несет информации о том, находится ли полученная оценка в середине распределения и, следовательно, является точной или в «хвосте» распределения и, таким образом, относительно неточна.

      Чем больше дисперсия случайного члена, тем, очевидно, больше будет выборочная дисперсия остатков и, следовательно, существеннее стандартные ошибки коэффициентов в уравнении регрессии, что позволяет с высокой вероятностью заключить, что полученные коэффициенты неточны. Однако это всего лишь вероятность. Возможно, что в какой-то конкретной выборке воздействия случайного фактора в различных наблюдениях будут взаимно погашены и в конечном итоге коэффициенты регрессии будут точны. Проблема состоит в том, что, вообще говоря, нельзя утверждать, произойдет это или нет.

Теорема Гаусса-Маркова

 Итак, мы имеем набор данных. Наша задача оценить все параметры модели : a, b, .

      Мы хотим оценить параметры “наилучшим” образом. Что означает “наилучшим”? Например, найти в классе несмещенных линейных оценок наилучшую в смысле минимальой дисперсии. Заметим, что когда такая оценка найдена, это вовсе не означает, что не существует нелинейной несмещенной оценки с меньшей дисперсией. Кроме того, наприме, можно отбросить требование несмещенности. И минимизировать среднеквадратическое отклонение оценки от истинного значения: .

      Теорема Гаусса-Маркова гласит, что в предположении четырех условий, рассмотреных в предыдущей главе, оценки , полученные по методу наименьших квадратов (МНК) имеют наименьшую дисперсию в классе всех линейных оценок несмещенных оценок.

      В данном изложении доказательство приводится не будет. Желающие могут ознакомиться с доказательством теоремы в лекциях С. С. Валландера.