Понятие системы

Система – это множество элементов с заданными отношениями иера­рхической подчиненности между ними. В системе выделяется главное, ос­новное и не основное. Системные отношения выстраивают структур­ные уровни по их важности, называемые таксонами, что осо­бенно характерно для социальных, экономических систем и группи­ровок в животном мире. Не всякая система имеет четко выраженную структуру, но структура часто бывает элементом системы. Систему может определять «организующий принцип» Очевидно, что для системы существенным фактором является не как элемент соотносится с другим элементом, а какое место занимает элемент в системе, важна не совокупность элементов, а их «целостность».

Солнечная система

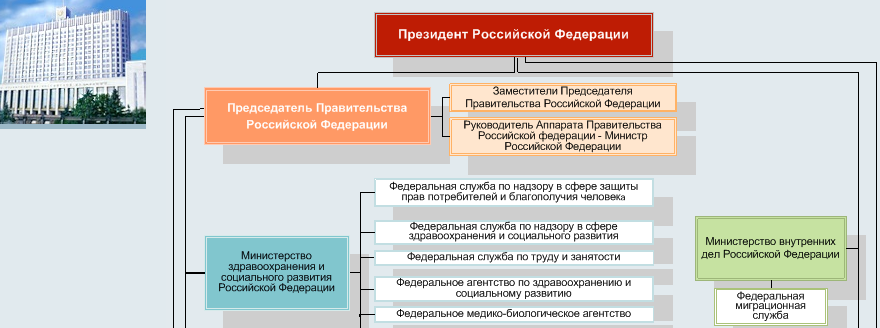
Федеральные органы исполнительной власти (фрагмент)

Рост структур и эволюция

Под рождением структуры будем понимать возникновение свя­зей между ее элементами при выходе из бесструктурного состояния. Гибель структуры, это, соответственно, обратный процесс перехода элемен­тов структуры в бесструктурное состояние хаоса. Структура изме­няется, если меняются характеристики параметров связи либо без их перестройки, либо при сохранении основной части параметров. Нако­нец, превращение структуры определяется изменением отношений связи между элементами. Происходит перестройка структуры (фазовый переход).

Увеличение количества элементов в системе с сохранением основных типов взаимодействия между ними характеризует процесс рос­та.

Математические модели роста (5 примеров).

1. Рост клеток.

Кривая состоит из трех частей: I - период, называемый Лаг - фазой, в течение которого идут под­готовительные (накопительные) процессы; II - период истинного роста, называемый экспоненциальной или логарифмической фазой и III - период, в течение которого рост клеток прекращается и попу­ляция вступает в стационарную фазу.

Нелинейное дифференциальное уравнение

может описывать рост "популяции" и в нем соотношение между коэффициентами "размножения" (a) и «потерь» (b) является ре­шающим.

2. Численность населения Земли

1. Геометрическая модель послойного роста кристаллов

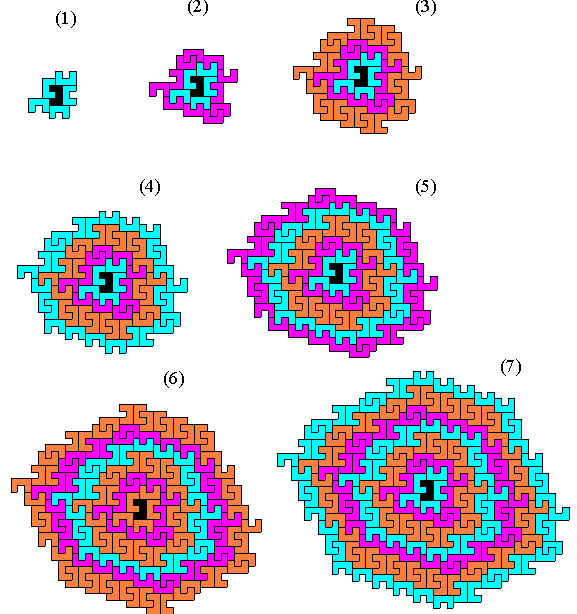
Поэтапное развитие структуры

3. Эволюционное дерево (граф).

5.Рост накоплений в пенсионном фонде

Из курса математики в разделе «пределы» установлено, что сумма накоплений в пенсионном фонде за n – лет определяется по формуле:

S = P₀( 1 + q + q² + q³ + …+ q^n-1), где P₀ – первоначальный вклад , а величина q = 1 + r/100 определяется процентной ставкой. Таким же образом, в изображенной мозаике количество пятиугольников поэтапно (слоями) разрастается по закону:

S = P₀(1 + q + q² + …+ q^n-1), где P₀ = 5, а q = 6.

Геометрическая модель финансовых накоплений

Энтропия и информация

Понятие энтропии как меры хаоса в системе возникло в молекулярной физике при анализе теплового (броуновского) движения частиц. При тепловом равновесии газа его макросостояние определяется средней энергией движения молекул, то есть постоянной температурой. В то же время энергия хаотического движения отдельных молекул все время меняется, их микросостояние не остается постоянным.

Таким же образом, в условиях рынка, доход каждого участника всегда характеризуется некоторой неопределенностью, мерой которой является вероятность или частота события. Фиксированная экспериментально доля людей с большими, средними или малыми доходами определяет эти вероятности. Следует ожидать, что доля участников с малыми и большими доходами невелика, а со средними – наибольшая. Это позволяет построить частотное распределение людей по величине дохода графически.

(ΔN/N)-доля людей

R_с

Шкала доходов (R)

Вид зависимости почти не изменяется со временем в условиях стабильности рынка или, как говорят физики, в условиях динамического равновесия. Макроэкономические параметры, такие как средний доход R_с,, при равновесии не меняются. Микроизменения с макроэкономическим равновесием могут сочетаться только в том случае, если люди не просто меняют свой доход, а обмениваются «местами» на шкале доходов, т.е. происходит случайная перестановка участников. Очевидно, что чем большее число микроизменений будет соответствовать определенному макросостоянию (с неизменными средними параметрами), чем больше случайных перестановок местами совершают участники рынка, тем больше хаоса заключено в таком макросостоянии. Обозначим количество микросостояний, соответствующих определенному макросостоянию символом W_T. Очевидно, что эта величина характеризует хаос. В состоянии равновесия она принимает наибольшее значение.

Действительно, если W_T = 1, никакого хаоса не будет, будет жестко определенное единственное состояние. Введем численную меру хаоса S ~ lnW_T, которая будет равна нулю (нет хаоса) при W_T = 1. Она называется энтропией, а выражение: S = k lnW_T является формулой Больцмана для энтропии.

Экспериментально установлено, что сложные системы (с большим числом элементов) самопроизвольно переходят из неравновесного в состояние равновесия, то есть в состояние хаотическое. Для изолированных систем этот экспериментальный факт выполняется всегда. В молекулярной физике и термодинамике его называют вторым законом термодинамики. В замкнутой системе хаос побеждает! «Побеждает» и энтропия, так как при переходе системы в состояние равновесия, энтропия становится наибольшей. Физик Клаузиус, опираясь на II – й закон термодинамики, высказал предположение, что наша Вселенная рано или поздно придет в состояние хаоса, в ней будут отсутствовать упорядоченные движения, направленные процессы. Такое состояние было названо «тепловой смертью Вселенной». Нобелевским лауреатом Пригожиным было показано, что существуют условия при которых из хаоса могут зарождаться упорядоченные структуры. Для этого система должна стать «открытой», то есть должна обмениваться с другими системами энергией и информацией. При получении и рецептировании информации энтропия уменьшается. Таким образом, любая система, в том числе и государство и человек, обязаны для своего существования развивать образовательный процесс, при котором накапливается и генерируется новая ценная информация. Простой пример.

При бросании кубика (игральной кости) существует неопределенность получения результата, так как 6 вариантов состояний равноправны: W_T = 6. До получения дополнительной информации S₁ = k ln 6. Если получена информация, что при бросании кубика выпало четное число, то неопределенность уменьшилась, так как таких состояний только 3, а величина энтропии стала равной S₂ = k ln 3. Очевидно, что она также уменьшилась. В природе существует много примеров таких процессов, когда из хаоса рождаются структуры при определенных условиях.

Снежинки при Охлаждении