12.4. Сортировки на деревьях
Простейший вид сортировки на деревьях уже упоминался: — это построение упорядоченного дерева и последовательное взятие значений узлов при обходе Слева направо.
Однако существуют и более эффективные сортировки, использующие древовидную структуру.
12.4.1. Турнирная сортировка
Идея турнирной сортировки фактически заимствована у организаторов спортивных чемпионатов. Участники соревнований разбиваются на пары, в которых разыгрывается первый тур; из победителей первого тура составляются пары для розыгрыша второго тура и т.д. Определяется победитель. При этом на каждом этапе сохраняется информация, полученная на предыдущих этапах, и для того, чтобы определить участника, занявшего второе место в турнире, нет нужды заново соревноваться всем оставшимся участникам.
Поэтому алгоритм сортировки состоит из двух шагов. Сначала строится дерево, аналогичное схеме розыгрыша кубка. Такое дерево представлено на форме, показанной на рис. 12.13.
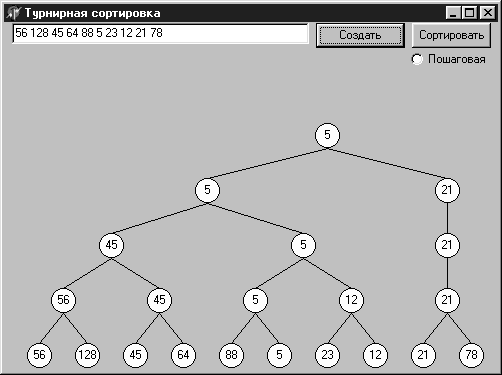
Рис. 12.13. Исходное дерево турнирной сортировки
На форме выставлены компоненты:
компонент Edit, предназначенный для ввода данных;
кнопка Создать, при нажатии на которую строится исходное турнирное дерево, имеющее вид пирамиды, и отображается на форме;
кнопка Сортировать, при нажатии на которую выполняется выбор значения с вершины дерева и перестройка дерева;
компонент RadioButton, установка которого позволяет по шагам проследить процесс сортировки.
Построение пирамиды выполняется функцией HeapCreate. Пирамида строится от основания к вершине. Элементы, составляющие каждый уровень, связываются в линейный список, поэтому каждый узел дерева помимо обычных указателей на сыновей — left и right — содержит и указатель на брата — next. При работе с каждым уровнем указатель pLevel содержит начальный адрес списка элементов в данном уровне. В первой фазе строится линейный список для нижнего уровня пирамиды, в элементы которого заносятся ключи из исходной последовательности. Следующий цикл while в каждой своей итерации надстраивает следующий уровень пирамиды. Условием завершения этого цикла является получение списка, состоящего из единственного элемента, то есть вершины пирамиды. Построение очередного уровня состоит в попарном переборе элементов списка, составляющего предыдущий (нижний) уровень. В новый (верхний) уровень переносится наименьшее значение ключа из каждой пары.
Для построения пирамиды необходимо, чтобы все значения были известны. Поэтому вводимые значения считываются из компонента Edit и заносятся в массив. При построении пирамиды одновременно производится рисование ее на форме. В листинге 12.11 приведены необходимые описания, обработчик события нажатия кнопки Создать и функция HeapCreate, строящая и рисующая пирамиду.
Листинг 12.11. Создание и рисование турнирной пирамиды
const M =50; // максимальный размер массива
N:integer=20; // число введенных элементов
type TKey = integer;
PNode = ^TNode;
TNode = record // узел дерева
key : TKey; // данные
Left,Right: PNode; // указатели на сыновей
Next : PNode; // указатель на брата
xN,yN : integer; // координаты узла для рисования
end;
Arr=array[1..M] of integer; // массив исходных значений
const diametr = 25;
radius = diametr div 2;
Geom = 1.5;
var
a : Arr;
Head : PNode;
x,y : integer; // координаты узла дерева-пирамиды
DrawingStep: Boolean; // разрешается ли рисование дерева
deltaX : integer; // расстояние между узлами по оси x
deltaY : integer; // расстояние между узлами по оси y
p : PNode;
xx,yy, delt: integer; // координаты узла и расстояние между
// узлами на нижнем уровне пирамиды
function TForm1.HeapCreate(a: Arr): PNode;
// Создание дерева-пирамиды -
// функция возвращает указатель на вершину
var i : integer;
pLevel : PNode; // адрес начала списка уровня
pNew : PNode; // адрес нового элемента
pOld : PNode; // адрес предыдущего элемента
comp1, comp2 : PNode;// адреса соревнующейся пары
begin
with canvas do begin
Brush.Style:=bsSolid;
Brush.Color:=clBtnFace;
FillRect(Rect(0,0,Width,Height));
end;
// *** построение самого нижнего уровня пирамиды ***
x:=deltaX; y:=Height-diametr-deltaY;
// создание первого элемента
new(pLevel);
with pLevel^ do begin
key:=a[1];
left:=nil; right:=nil; // потомков нет
xN:=x; yN:=y;
end;
DrawNode(x,y, IntToStr(a[1]), false);
pOld:=pLevel;
// включение в список остальных элементов массива
for i:=2 to N do begin
New(pNew);
x:=x+deltaX+diametr;
DrawNode(x,y, IntToStr(a[i]), false);
with pNew^ do begin
key:=a[i];
left:=nil; right:=nil; // потомков нет
xN:=x; yN:=y;
end;
pOld.next:=pNew; // связывание в линейный список по уровню
pOld:=pNew;
end;
pNew.next:=nil;
// построение других уровней
while pLevel.next<>nil do begin { цикл до вершины пирамиды }
y:=y-deltaY-diametr;
comp1:=pLevel; pLevel:=nil; { начало нового уровня }
while comp1<>nil do begin { цикл по очередному уровню }
comp2:=comp1.next;
New(pNew);
// адреса потомков из предыдущего уровня
pNew.left:=comp1; pNew.right:=comp2;
pNew.next:=nil; pNew.xN:=x; pNew.yN:=y;
// связывание в линейный список по уровню
if pLevel=nil then pLevel:=pNew else pOld^.next:=pNew;
pOld:=pNew;
// состязание данных за выход на уровень
if (comp2=nil) or (comp2.key>comp1.key) then begin
pNew.key:=comp1.key;
end
else pNew.key:=comp2.key;
if comp2=nil then x:= comp1.xN
else x:=(comp1.xN+comp2.xN)div 2;
with pNew^ do begin
xN:=x; yN:=y;
end;
// рисование узла и ветвей
DrawNode(x,y, IntToStr(pNew.key), false);
with Form1.Canvas do begin
if pNew.left<>NIL then begin
MoveTo(x+radius,y+diametr);
LineTo(pNew.left.xN+radius,pNew.left.yN);
end;
if pNew.right<>NIL then begin
MoveTo(x+radius,y+diametr);
LineTo(pNew.right.xN+radius,pNew.right.yN);
end;
end;
// переход к следующей паре
if comp2<>nil then comp1:=comp2.next else comp1:=nil;
end; // while comp1<>nil
end; // while comp2.next<>nil
HeapCreate:=pLevel;
end;
procedure TForm1.BtnCreateClick(Sender: TObject);
var ph : PNode;
i, num : integer;
s : String;
LenS : integer; // длина строки
begin
// формирование массива значений
s:=EdtIn.Text; LenS:=length(s);
i:=1; N:=0;
while i<=LenS do begin
while s[i]=' ' do inc(i); num:=0;
while s[i] in ['0'..'9'] do begin
num:=10*num+ord(s[i])-ord('0');
inc(i);
end;
inc(N); a[N]:=num;
end;
// расчет положения пирамиды на форме
deltaX:=round((Width-N*diametr)/(N+1));
i:=round(ln(N)/ln(2));
deltaY:=30;
// построение и отображение пирамиды
Head:=HeapCreate(a);
delt:=round(Width - N*diametr - 80)div (n+1);
xx:=delt; yy:=30;
end;
Процедура DrawNode — процедура рисования узла та же, что и в программе рисования упорядоченного дерева. Она дополнена еще одним параметром, учитывающим цвет узла.
Следующий этап состоит в выборке значений из вершины пирамиды и формирования из них упорядоченной последовательности. Значение в вершине пирамиды — это наименьшее из имеющихся в пирамиде значений ключа. Узел‑вершина при этом освобождается, освобождаются также и все узлы, занимаемые выбранным значением на более низких уровнях пирамиды. За освободившиеся узлы устраивается (снизу вверх) состязание между их потомками. Так, для пирамиды, исходное состояние которой было показано на рис 12.13, при выборке первых трех ключей (5 12 21) пирамида будет последовательно принимать вид, показанный на рис. 12.14а, б и в. Удаленные узлы содержат последние находящиеся в них значения и отмечены только контуром.
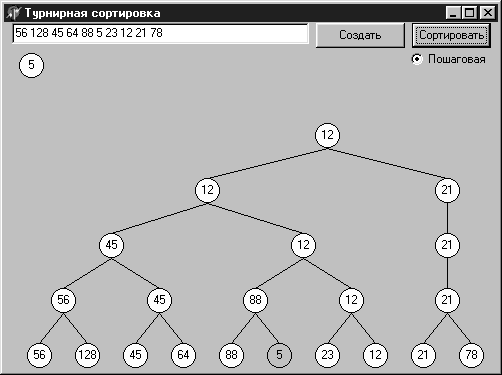
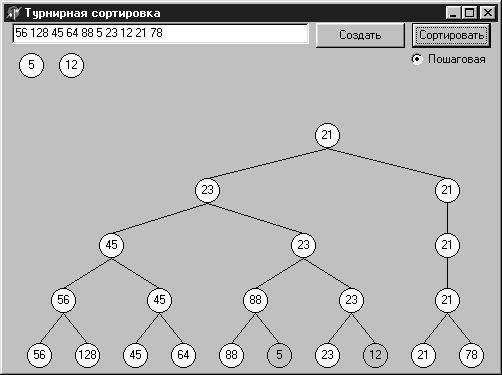
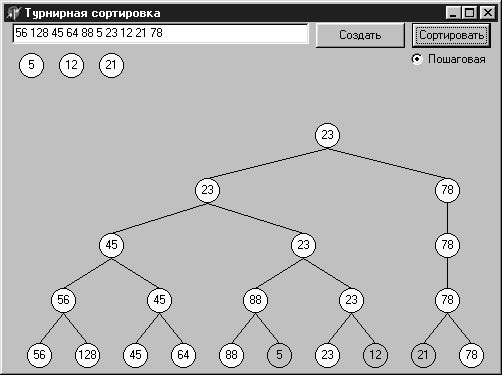
Рис. 12.14. Выборка значений из турнирной пирамиды
Обработчик события нажатия кнопки Сортировать имеет две ветви: пошаговой выборки значений из вершины пирамиды и выборки всех значений, осуществляемой циклом. После каждой выборки из вершины пирамида подлежит реорганизации, которая осуществляется функцией Competition.
Функция Competition рекурсивная, ее параметром является указатель на вершину того поддерева, которое подлежит реорганизации. Сначала функция определяет, есть ли у узла, составляющего вершину заданного поддерева, сын, значение данных в котором совпадает со значением данных в вершине. Если такой сын есть, то функция Competition вызывает сама себя для реорганизации того поддерева, вершиной которого является обнаруженный сын. После реорганизации адрес сына в узле заменяется тем адресом, который вернул рекурсивный вызов Competition. Если после реорганизации оказывается, что у узла нет детей (или он не имел детей с самого начала), то узел уничтожается и функция возвращает указатель, равный Nil. Если же у узла еще остаются сыновья, то в поле данных узла заносится значение данных из того сына, в котором это значение наименьшее, и функция возвращает прежний адрес узла.
Функция Competition и обработчик события нажатия кнопки Сортировать приведены в листинге 12.12.
Листинг 12.12. Реорганизация турнирной пирамиды
function TForm1.Competition(ph : PNode): PNode;
// Реорганизация поддерева
begin
// определение наличия потомков, выбор сына для
// реорганизации, реорганизация его
if ph.left<>nil then begin
if ph.left.key=ph.key then ph.left:=Competition(ph.left)
else ph.right:=Competition(ph.right);
end
else
if ph.right<>nil then ph.right:=Competition(ph.right);
if (ph.left=nil) and (ph.right=nil) then begin
DrawNode(ph.xN,ph.yN, IntToStr(ph.key), true);
Dispose(ph); ph:=nil; // освобождение пустого узла
end
else
// состязание данных сыновей
if (ph.left=nil)
or((ph.right<>nil)
and (ph.left.key>ph.right.key)) then begin
ph.key:=ph.right.key;
DrawNode(ph.xN,ph.yN, IntToStr(ph.key), false);
sleep(500);
DrawNode(ph.xN,ph.yN, IntToStr(ph.key), true);
sleep(500);
DrawNode(ph.xN,ph.yN, IntToStr(ph.key), false);
end
else begin
ph.key:=ph.left.key;
DrawNode(ph.xN,ph.yN, IntToStr(ph.key), false);
sleep(500);
DrawNode(ph.xN,ph.yN, IntToStr(ph.key), true);
sleep(500);
DrawNode(ph.xN,ph.yN, IntToStr(ph.key), false);
end;
Competition:=ph;
end;
procedure TForm1.BtnSortClick(Sender: TObject);
var i: integer;
begin
if DrawingStep then begin
if Head <> NIL then begin
DrawNode(xx,yy, IntToStr(Head.key), false);
Head:=Competition(Head); // реорганизация дерева
xx:=xx+delt+diametr;
sleep(1000);
end;
end
else begin
if Head <> NIL then begin
for i:=1 to N do begin
DrawNode(xx,yy, IntToStr(Head.key), false);
Head:=Competition(Head); // реорганизация дерева
xx:=xx+delt+diametr;
sleep(1000);
end;
end;
end;
end;
Рассматривая эффективность турнирной сортировки, следует отметить, что построение дерева требует N – 1 сравнений, выборка — N×log2(N) сравнений. Порядок алгоритма — N×log2(N). Сложность операций над динамическими структурами данных, однако, значительно выше, чем над статическими структурами. Кроме того, алгоритм неэкономичен в отношении памяти: дублирование данных на разных уровнях пирамиды приводит к тому, что рабочая область памяти содержит примерно 2×N узлов.