12.2.2. Поиск по дереву с включением
Вернемся теперь к задаче о построении частотного словаря, рассмотренной в главе 10. В этой задаче задана последовательность слов, и нужно установить число появлений каждого слова. С помощью упорядоченного дерева эту задачу можно решить следующим образом. Начиная с пустого дерева, каждое слово ищется в дереве. Если слово найдено, увеличивается его счетчик повторений, если нет — в дерево вставляется новое слово (с начальным значением счетчика, равным 1). Эта задача называется поиск по дереву с включением. Алгоритм приведен в листинге 12.5.
Листинг 12.5. Поиск по дереву с включением
type Tkey = string;
TNode = ^PNode;
PNode = record
key : TKey; // слово
count: integer; // счетчик повторений
left, right: TNode;
end;
procedure Search(x: Tkey; var Tree: TNode);
begin
if Tree = Nil then begin // слова в дереве нет, включить его
new(Tree);
with Tree^ do begin
key:=x; count:=1;
left:=Nil; right:=Nil
end
end
else
if x < Tree^.key then Search(x,Tree^.left) // ищем слева
else
if x > Tree^.key then Search(x,Tree^.right) // ищем справа
else inc(Tree^.count) // увеличиваем счетчик
end;
Представляется интересным сравнить две процедуры: Insert — вставки всех значений в упорядоченное дерево и Search — поиска и включения только новых значений.
Итак, если есть упорядоченное дерево, то его можно применять как для сортировки, так и для поиска.
Действительно, поиск значения x осуществляется перемещением по дереву линейно, выбирая на каждом этапе направление дальнейшего движения — влево или вправо. Осуществляя обход дерева алгоритмом Слева направо получим значения узлов в порядке возрастания, то есть отсортированную последовательность.
12.2.3. Удаление из упорядоченного дерева
Задача, обратная включению, — удаление заданного узла из упорядоченного дерева. После операции удаления дерево должно остаться упорядоченным.
Рассмотрим последовательное удаление узлов из дерева, представленного на рис. 12.3.
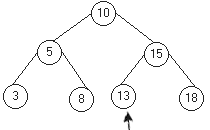
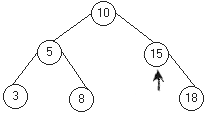
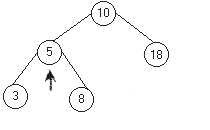
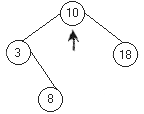
Рис. 12.3. Удаление из упорядоченного дерева
Удаление из упорядоченного дерева не всегда такое простое, как включение. Оно является простым в случае, когда удаляемый узел — лист (а). Тогда лист просто удаляется. Если удаляемый узел имеет только одного сына, то удаляемый узел заменяется узлом‑сыном (б). Трудность заключается в удалении узла с двумя сыновьями, поскольку невозможно указать одной ссылкой два направления. В этом случае удаляемый узел нужно заменить либо на самый правый элемент его левого поддерева, либо на самый левый элемент его правого поддерева. Ясно, что такие элементы не могут иметь более одного потомка. Деревья, полученные последовательным удалением узлов 13, 15, 5, 10 из дерева на рис. 12.3(а), показаны на рис. 12.3(б – д) .
Алгоритм удаления узла с ключом x из упорядоченного дерева реализован процедурой Delete, приведенной в листинге 12.6.
Процедура различает три случая:
в дереве нет узла с ключом x;
узел с ключом x имеет не более одного сына;
узел с ключом x имеет двух сыновей.
Листинг 12.6. Удаление из упорядоченного дерева
procedure TForm1.Delete(x: Tkey; var Tree: TNode; var moving:Boolean);
var q: TNode;
procedure Del(var r: TNode);
begin
if r^.right <> Nil then
Del(r^.right)
else begin
q^.key:=r^.key;
q:=r; r:=r^.left;
end;
end;
begin
if Tree = Nil then moving:=false
else
if x < Tree^.key then Delete(x, Tree^.left, moving)
else
if x > Tree^.key then Delete(x, Tree^.right, moving)
else begin // удаление узла
moving:=true;
q:=Tree;
if q^.right = Nil then Tree:=q^.left
else
if q^.left = Nil then Tree:=q^.right
else del(q^.left);
dispose(q);
end;
end;
Вспомогательная рекурсивная процедура del вызывается только в случае, когда удаляемый узел имеет двух сыновей. Она "спускается" вдоль самой правой ветви левого поддерева удаляемого узла q^ и затем заменяет ключ в q^ соответствующим значением самого правого узла r^ этого левого поддерева. После чего r^ удаляется.
Параметр‑переменная moving передает сведения о том, был ли удален требуемый узел Он принимает значение true, если узел был найден и удален, и false в противном случае.
На рис. 12.4 представлена форма создания и рисования дерева, дополненная кнопкой Удалить узел.
Рисунок 12.4. Форма удаления из упорядоченного дерева
На рис. 12.4.а видно, что удаляется корневой узел — 8. После удаления значение корня становится равным 7 — значению самого правого узла левого поддерева корня (б).
Обработчик события нажатия кнопки Удалить узел приведен в листинге 12.7.
Листинг 12.7. Обработчик события нажатия кнопки Удалить узел
procedure TForm1.Button1Click(Sender: TObject);
var mov: Boolean; // признак удаления узла
xDel: integer; // значение удаляемого узла
begin
xDel:=StrToInt(EdtIn.Text); // формирование значения
Delete(xDel, Tree, mov); // удаление узла
if mov then begin
with canvas do begin
Brush.Style:=bsSolid;
Brush.Color:=clBtnFace;
FillRect(Rect(0,0,Width,Height)); // очистка формы
end;
DrawTree(Tree,Tree.xN,Tree.yN) // рисование нового дерева
end
else ShowMessage('Такого узла нет!');
end;
Понятно, что форма упорядоченного дерева зависит от порядка добавления элементов. На рис. 12.5 показаны два различных упорядоченных дерева, построенных из одинаковых элементов, поступающих в разном порядке.
Рис. 12.5. Деревья, построенные при различном порядке поступления элементов
Высокие, тонкие деревья, как на рис. 12.5 а, могут иметь высоту ~N. Добавление элемента в такое дерево или поиск в нем могут потребовать ~N операций, поэтому такие деревья, представляющие собой сложную форму списка, неэффективны для работы. Для эффективного использования древовидной структуры желательно иметь упорядоченные и сбалансированные деревья.