Глава 12. Деревья

В главе 11 рассматривались рекурсивные определения и рекурсивные алгоритмы. Теперь рассмотрим структуры данных, определяемые с помощью рекурсии. Среди таких структур наиболее важными являются деревья.

Рис. 12.1. Эшер М. Три мира (фрагмент).

Деревья наилучшим образом приспособлены для решения задач искусственного интеллекта и синтаксического анализа.

12.1. Понятия и определения

Древовидная структура (дерево) определяется следующим образом: дерево (tree) с базовым типом T — это либо

• пустая структура; либо

• узел типа T, с которым связано конечное число древовидных структур, называемых поддеревьями (subtree).

Если с узлом связаны только два поддерева, то дерево называется бинарным. В этой главе будут рассматриваться только бинарные деревья.

Дерево обычно изображается так, как показано на рис. 12.2.

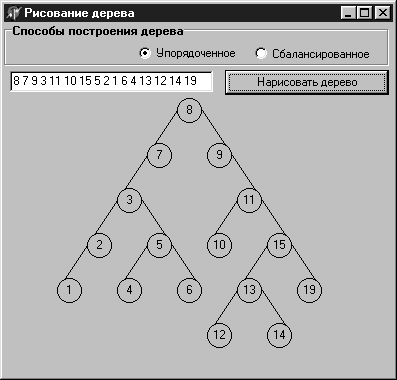
Рис. 12.2. Представление дерева

Деревья в информатике принято рисовать перевернутыми — растущими вниз. Или их можно рассматривать словно отраженными в воде, как на рис. 12.1.

Терминология, применяемая для описания деревьев, представляет собой смесь терминов, взятых как из ботаники, так и из генеалогии. Из ботаники взяты определения:

• узел (node) — это точка, где может возникнуть ветвь. На рис. 12.2 узлы — это, например, и ;

• корень (root) — верхний узел дерева. Для дерева на рис. 12.2 это — ;

• ветвь (brunch) — описывает связь между двумя узлами;

• лист (leaf) — узел, из которого не выходят ветви, то есть не имеющий поддеревьев. На рис. 12.2 листьями являются, например, , , и .

Термины, взятые из генеалогии, описывают отношения:

• родительским (parent) называется узел, который находится непосредственно над другим узлом;

• дочерним (child) называется узел, который находится непосредственно под другим узлом; дочерний узел также называют сыном (что не меняет "родственности" отношений);

• предки данного узла — все узлы на пути вверх от данного узла до корня. Например, предками узла являются узлы , и ;

• потомки — все узлы, расположенные ниже данного. Для узла узлами‑потомками являются: , , и ;

• сестринские (братские) — узлы, у которых один и тот же родитель. Братьями являются, например, и , и .

Термины, возникшие в программировании:

• внутренний узел (internal node) — узел, не являющийся листом;

• порядок узла (node degree) — количество его дочерних узлов;

• глубина(depth) узла — количество его предков плюс единица;

• глубина(высота) дерева — максимальная глубина всех узлов;

• длина пути к узлу — количество ветвей, которые нужно пройти, чтобы продвинуться от корня к данному узлу;

• длина пути дерева — сумма длин путей всех его узлов. Она также называется длиной внутреннего пути.

12.2. Основные операции с бинарными деревьями

В программировании, как и в природе, все деревья, даже одной породы, — разные: они отличаются количеством и направлением ветвей, количеством листьев. При работе программы дерево может модифицироваться: добавляются или удаляются узлы, меняются информационные части узлов. То есть дерево является динамической структурой. Поэтому узел дерева определяется как переменная с фиксированной структурой, содержащей информационную часть и две ссылки, указывающие на левое и правое поддерево данного узла. Ясно, что ссылка на пустое дерево равна Nil.

Описание узла дерева:

type TKey=integer; // тип информационного поля

TNode=^PNode;

PNode=record

key : TKey; // значение ключа

left, right: TNode; // ссылки на левое и правое поддеревья

end;

Динамический способ представления дерева — не единственно возможный, дерево можно также представить с помощью массива. Элементы массива будут содержать значения узлов дерева, а с помощью индексов можно установить структуру дерева. Так, в первом элементе, i = 1, хранится значение корня. Элемент с i = 2 хранит значение левого сына корня, элемент с i = 3 хранит значение правого сына корня. И так для любого элемента с индексом i индекс его левого сына равен 2×i, а правого — 2 × i +1. Индекс отца будет равен i div 2. Однако так можно хранить деревья со строго определенной структурой. Ниже будет рассмотрен пример сортировки частично упорядоченным деревом, представленным массивом. Для деревьев произвольной формы в массив приходится заносить специальные значения, соответствующие Nil, если у какого-то узла отсутствует тот или иной сын, или для каждого узла хранить индексы его сыновей. Так, в таблице 12.1 приведен массив, хранящий дерево, представленное на рис. 12.2. Верхняя строка содержит индексы массива, вторая строка — значения ключей, а третья и четвертая строки — индексы левого и правого сыновей. Значение 0 соответствует отсутствию сына.

Таблица 12.1. Дерево, представленное с помощью массива

Индекс	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
Ключ	8	7	9	3	11	2	5	10	15	1	4	6	13	19	12	14
Левый	2	4	0	6	8	10	11	0	13	0	0	0	15	0	0	0
Правый	3	0	5	7	9	0	12	0	14	0	0	0	16	0	0	0

В связи с двоичными деревьями (и деревьями вообще) вводится важная категория алгоритмов: алгоритмы обхода дерева. Такой алгоритм — это метод, который позволяет получить доступ к каждому узлу дерева один и только один раз.

Для каждого узла выполняются некоторые виды обработки (проверка, суммирование и т.п.), однако способ обхода не зависит от конкретных действий и является общим для всех алгоритмов обработки узлов.

Отдельные узлы посещаются в некотором определенном порядке.

Существуют три порядка, использующие обход в глубину:

1. Сверху вниз (PreOrder):

• обработать корень;

• обход левого поддерева;

• обход правого поддерева;

2. Слева направо (PostOrder):

• обход левого поддерева;

• обработать корень;

• обход правого поддерева;

3. Снизу вверх(InOrder):

• обход левого поддерева;

• обход правого поддерева;

• обработать корень.

Четвертый порядок обхода узлов дерева можно назвать обходом в ширину. В этом случае сначала обращаются ко всем узлам на данном уровне дерева, а затем переходят к следующему уровню. Обход в ширину часто используется в алгоритмах, осуществляющий полный поиск в дереве. Наиболее прост алгоритм обхода в ширину при представлении дерева в виде массива — это цикл по всем элементам.

Для дерева, представленного на рис. 12.2, четыре способа обхода дают следующий результат:

1. 8 7 3 2 1 5 4 6 9 11 10 15 13 12 14 19

2. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 19

3. 1 2 4 6 5 3 7 10 12 14 13 19 15 11 9 8

4. 8 7 9 3 11 2 5 10 15 1 4 6 13 19 12 14

Первые три метода легко представить в виде рекурсивных процедур. Процедуры просты, и это свидетельство того, что рекурсивные структуры естественнее всего описывать рекурсивными алгоритмами.

Процедуры представлены в листинге 12.1. Процедура Proc — некоторая процедура обработки узла. Учитывается приведенное выше описание узла дерева.

Листинг 12.1. Процедуры обхода дерева

procedure PreOrder(Tree: TNode); // Сверху вниз

begin

if Tree <> Nil then begin

Proc(Tree^); // обработка узла

PreOrder(Tree^.left);

PreOrder(Tree^.right);

end;

end;

procedure InOrder(Tree: TNode); // Слева направо

begin

if Tree <> Nil then begin

InOrder(Tree^.left);

Proc(Tree^); // обработка узла

InOrder(Tree^.right);

end;

end;

procedure PostOrder(Tree: TNode); // Снизу вверх

begin

if Tree <> Nil then begin

PostOrder(Tree^.left);

PostOrder(Tree^.right);

Proc(Tree^); // обработка узла

end;

end;

Примечание

Следует обратить внимание, что ссылка Tree передается как параметр‑значение. Это отражает тот факт, что здесь существенна сама ссылка (указатель) на рассматриваемое поддерево, а не переменная, значение которой есть эта ссылка и которая могла бы изменить значение, если бы Tree передавалась как параметр-переменная.

Пример процедуры, осуществляющий обход дерева, приведен ниже, в листинге 12.4. Обход дерева осуществляется с целью найти ближайший к указателю мышки узел нарисованного на канве дерева.