Код Шеннона-Фано

Основные этапы

1. Символы первичного алфавита m₁ выписывают в порядке убывания вероятностей.

2. Символы полученного алфавита делят на две части, суммарные вероятности символов которых максимально близки друг другу.

3. В префиксном коде для первой части алфавита присваивается двоичная цифра «0», второй части — «1».

4. Полученные части рекурсивно делятся и их частям назначаются соответствующие двоичные цифры в префиксном коде.

Когда размер под алфавита становится равен нулю или единице, то дальнейшего удлинения префиксного кода для соответствующих ему символов первичного алфавита не происходит, таким образом, алгоритм присваивает различным символам префиксные коды разной длины. На шаге деления алфавита существует неоднозначность, так как разность суммарных вероятностей   может быть одинакова для двух вариантов разделения (учитывая, что все символы первичного алфавита имеют вероятность больше нуля).

Алгоритм вычисления кодов

Код Шеннона — Фано строится с помощью дерева. Построение этого дерева начинается от корня. Всё множество кодируемых элементов соответствует корню дерева (вершине первого уровня). Оно разбивается на два подмножества с примерно одинаковыми суммарными вероятностями. Эти подмножества соответствуют двум вершинам второго уровня, которые соединяются с корнем. Далее каждое из этих подмножеств разбивается на два подмножества с примерно одинаковыми суммарными вероятностями. Им соответствуют вершины третьего уровня. Если подмножество содержит единственный элемент, то ему соответствует концевая вершина кодового дерева; такое подмножество разбиению не подлежит. Подобным образом поступаем до тех пор, пока не получим все концевые вершины. Ветви кодового дерева размечаем символами 1 и 0, как в случае кода Хаффмана.

При построении кода Шеннона — Фано разбиение множества элементов может быть произведено, вообще говоря, несколькими способами. Выбор разбиения на уровне n может ухудшить варианты разбиения на следующем уровне (n + 1) и привести к неоптимальности кода в целом. Другими словами, оптимальное поведение на каждом шаге пути ещё не гарантирует оптимальности всей совокупности действий. Поэтому код Шеннона — Фано не является оптимальным в общем смысле, хотя и дает оптимальные результаты при некоторых распределениях вероятностей. Для одного и того же распределения вероятностей можно построить, вообще говоря, несколько кодов Шеннона — Фано, и все они могут дать различные результаты. Если построить все возможные коды Шеннона — Фано для данного распределения вероятностей, то среди них будут находиться и все коды Хаффмана, то есть оптимальные коды.

Пример кодового дерева

Исходные символы:

• A (частота встречаемости 50)

• B (частота встречаемости 39)

• C (частота встречаемости 18)

• D (частота встречаемости 49)

• E (частота встречаемости 35)

• F (частота встречаемости 24)

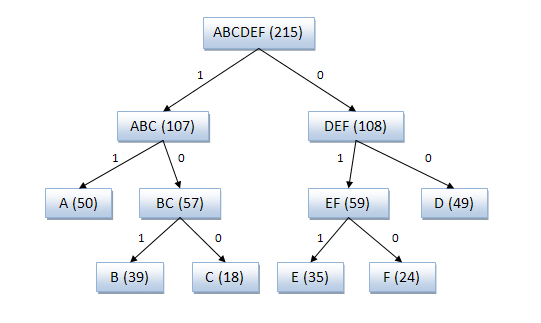
Кодовое дерево

Полученный код: A — 11, B — 101, C — 100, D — 00, E — 011, F — 010.

Код Хаффмана

Определение 1: Пусть A={a₁,a₂,_...,a_n} - алфавит из n различных символов, W={w₁,w₂,_...,w_n} - соответствующий ему набор положительных целых весов. Тогда набор бинарных кодов C={c₁,c₂,_...,c_n}, такой что:

(1) c_i не является префиксом для c_j, при i≠j

(2) минимальна (|c_i| длина кода c_i)

Называетсяминимально-избыточным префиксным кодом или иначе кодом Хаффмана.

Замечания:

1. Свойство (1) называется свойством префиксности. Оно позволяет однозначно декодировать коды переменной длины.

2. Сумму в свойстве (2) можно трактовать как размер закодированных данных в битах. На практике это очень удобно, т.к. позволяет оценить степень сжатия не прибегая непосредственно к кодированию.

3. В дальнейшем, чтобы избежать недоразумений, под кодом будем понимать битовую строку определенной длины, а под минимально-избыточным кодом или кодом Хаффмана - множество кодов (битовых строк), соответствующих определенным символам и обладающих определенными свойствами.

Известно, что любому бинарному префиксному коду соответствует определенное бинарное дерево.

Определение 2: Бинарное дерево, соответствующее коду Хаффмана, будем называть деревом Хаффмана.

Задача построения кода Хаффмана равносильна задаче построения соответствующего ему дерева. Приведем общую схему построения дерева Хаффмана:

буквы располагают в порядке убывания их вероятностей. Складывают вероятности двух последних букв, и ряд переписывают снова с учетом новой вероятности (суммы). Далее повторяют операцию, пока не получится 1. Нижнюю букву всегда кодируют нулем, а верхнюю – единицей.

Для составления кодовых комбинаций строится кодовое дерево. Двигаясь по кодовому дереву сверху вниз, можно записать для каждой буквы соответствующую ей кодовую комбинацию.

Код Хаффмана, также как и Шеннона-Фано является префиксным, то есть в таком коде ни одна комбинация не совпадает с началом более длинной комбинации, а это позволяет обеспечить однозначное декодирование без введения разделительных символов.

 

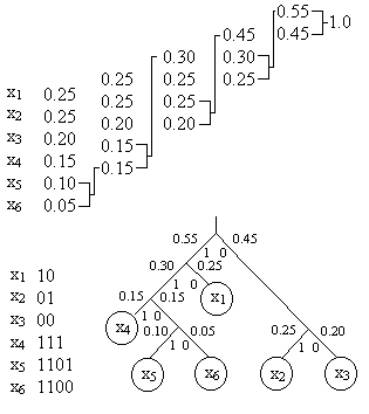
Среднее кол-во разрядов:

  

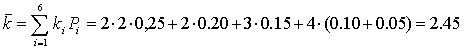
Энтропия

 

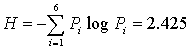
Как мы видим, величина среднего кол-ва разрядов получилась достаточно близкой к энтропии, следовательно, код можно считать эффективным. При этом для сравнения можно вычислить величину K для равномерного кода: 

1. ЗАДАЧА.

Пусть имеется случайная величина  X(x₁,x₂,x₃,x₄,x₅,x₆,x₇,x₈), имеющая восемь состояний  с распределением вероятностей

Закодировать буквы (x₁,x₂,x₃,x₄,x₅,x₆,x₇,x₈) в коде Шеннона-Фано.

Все буквы записываются в порядке убывания их вероятностей, затем делятся на равновероятные группы, которые обозначаются 0 и 1, затем вновь делятся на равновероятные группы и т.д.

2. ЗАДАЧА

построить дерево Хаффмана для сообщения S="AHFBHCEHEHCEAHDCEEHHHCHHHDEGHGGEHCHH".

УКАЗАНИЕ: в нашем случае A={A, B, C, D, E, F, G, H}, W={2, 1, 5, 2, 7, 1, 3, 15}.

3. ЗАДАЧА

Пусть имеется следующая таблица префиксных кодов:

а	л	м	р	у	ы
10	010	00	11	0110	0111

Требуется декодировать сообщение: 00100010000111010101110000110

УКАЗАНИЕ: Декодирование производится циклическим повторением следующих действий:

1. отрезать от текущего сообщения крайний левый символ, присоединить к рабочему кодовому слову;

2. сравнить рабочее кодовое слово с кодовой таблицей; если совпадения нет, перейти к (1);

3. декодировать рабочее кодовое слово, очистить его;

4. проверить, имеются ли еще знаки в сообщении; если «да», перейти к (1).

4. ЗАДАЧА

Пусть имеется первичный алфавит A, состоящий из шести знаков a₁ …a₆ с вероятностями появления в сообщении, соответственно, 0,3; 0,2; 0,2; 0,15; 0,1; 0,05.

Построить код Хаффмана

5. ЗАДАЧА

Закодируйте двоичным кодом Шеннона-Фано ансамбль сообщений Х = х1, х2, ..., х8, если все кодируемые сообщения равновероятны. Показать оптимальный характер полученного кода.

6. ЗАДАЧА

Определите количество элементов в кодовом слове, если известно общее число комбинаций N = 512, а основание кода 2.

7. ЗАДАЧА

Сколько двоичных чисел может быть представлено 7-разрядным кодом?

8. ЗАДАЧА

Дана совокупность символов х1, х2, х3, х4 со следующей статистикой соответственно: 0,28; 0,14; 0,48; 0,10. Закодируйте символы по методу Шеннона-Фано и определите эффективность кода.