Префиксные коды

Большинство кодов применяются для передачи и хранения информации без учета статистических характеристик поступающих сообщений. Учитывая статистические свойства источника сообщений, можно минимизировать среднюю длину кодовых сообщений.

Рассмотрим примеры кодирования. Понятно, что кодирование информации допускается тогда, когда возможно последующее однозначное декодирование 

Символ	Код1	Код2	Код3	Код4
x1	0	0	0	0
x2	0	00	01	10
x3	1	1	011	110
x4	11	11	0111	111

Видно, что код 1 не дает однозначного декодирования. Код 2, хотя и выражен более тонким образом, обладает тем же недостатком, так как при передаче последовательности x₁x_1, она будет закодирована в 00, что совпадает с кодовым словом для x₃. Коды 1 и 2 не являются, таким образом, различимыми. Код 3 также не позволяет производить однозначное декодирование. Однозначно декодируемыми являются только коды обладающие свойством префикса. 

Префиксные коды - это такие коды, в которых ни одна более короткая комбинация не является началом более длинной комбинации, а это позволяет производить однозначное декодирование, даже если последовательность кодов не содержит разделителей между кодами.

Коды 1,2,3 не обладают свойством префикса, а код 4 обладает.

Например, код  0111100 декодируется в последовательность символов x₁x₄x₂x₁.

Для  построения префиксных кодов используется двоичное дерево.  

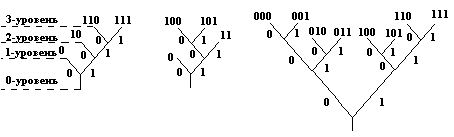
Разобьем дерево на уровни и тогда каждому коду можно присвоить определённый вес.

 - вес j-кода j=1,М, где М- число допустимых кодов, k - уровень дерева. Дерево может иметь и более двух ветвей D>2.

Тогда вес j - кода будет равен   , где D - основание системы счисления.

Оптимальное кодирование

Одно и то же сообщение можно закодировать различными способами. Оптимально закодированным будем считать такой код, при котором на передачу сообщений затрачивается минимальное время. Если на передачу каждого элементарного символа (0 или 1) тратиться одно и то же время, то оптимальным будет такой код, который будет иметь минимально возможную длину.

Пример 1.

Пусть имеется случайная величина  X(x₁,x₂,x₃,x₄,x₅,x₆,x₇,x₈), имеющая восемь состояний  с распределением вероятностей

Для кодирования алфавита из восьми букв без учета вероятностей равномерным двоичным кодом нам понадобятся три символа:

   Это         000, 001, 010, 011, 100, 101, 110, 111

Чтобы ответить, хорош этот код или нет, необходимо сравнить его с оптимальным значением, то есть определить энтропию

Определив избыточность L по формуле L=1-H/H₀=12,75/3=0,084,  видим, что возможно сокращение длины кода  на 8,4%.

Возникает вопрос: возможно ли составить код, в котором на одну букву будет, в среднем приходится меньше элементарных символов.

Такие коды существуют. Это коды ШеннонаФано и Хаффмана.

Принцип построения оптимальных кодов:

1.   Каждый элементарный символ должен переносить максимальное количество информации, для этого необходимо, чтобы элементарные символы (0 и 1) в закодированном тексте встречались в среднем одинаково часто. Энтропия в этом случае будет максимальной.

2.   Необходимо буквам первичного алфавита, имеющим большую вероятность, присваивать более короткие кодовые слова вторичного алфавита.