5.1.7. La courbe de demande collective d’un bien.

Quelque soit le nombre de demandeurs sur un marché, si leurs demandes individuelles sont bien définies, il suffit d’additionner les quantités qu’ils demandent aux différents prix pour obtenir la demande collective (ou sur un marché) pour ce bien. Celle-ci se définit donc comme la totalité des quantités alternatives d’un bien que l’ensemble des acheteurs sur un marché sont désireux d’acquérir en un temps donné aux divers prix possibles.

Une telle demande est fonction des mêmes variables que la demande individuelle mais elle dépend du nombre d’acheteurs potentiels sur le marché et donc indirectement de la population et de sa structure.

Si l’on considère 4 acheteurs hypothétiques dont les quantités demandées sont énumérées dans le tableau suivant, la quantité totale demandée sur le marché (la demande collective) est la somme des 4 demandes individuelles.

Prix sur le marché	Quantités demandées par unité de temps
	Individu 1	Individu 2	Individu 3	Individu 4	Marché
15	0	0	0	0	0
14	2	0	0	0	2
13	4	2	0	0	6
12	6	5	0	0	11
11	10	7	1	0	18
10	12	9	2	0	23
09	15	11	4	1	31
08	18	14	7	4	43
07	23	17	11	9	60
06	26	20	16	16	78
05	28	24	23	25	100

Graphiquement, cette agrégation des demandes individuelles se représente en traçant dans un même diagramme toutes les courbes de demande individuelles mais d’une marnière particulière : pour chacune d’elle l’abscisse (les quantités) est calculée à partir du niveau de consommation de la courbe précédente. La courbe la plus à droite est ainsi la courbe de demande collective.

On notera qu’en général, les demandeurs n’ont pas des courbes de demande individuelles identiques : selon les goûts et les préférences de chacun, la forme de chacune d’elle varie d’un individu à l’autre.

La courbe de demande sur le marché se déplace vers la droite ou vers la gauche dans deux catégories de cas : lorsqu’une ou plusieurs courbes de demande individuelles se déplace ou lorsque le nombre des demandeurs apparaissant sur le marché augmente ou diminue.

5.2. La courbe d’offre collective d’un bien.

5.2.1. Les choix des producteurs : production, coûts.

La première question que soulève l’analyse de l’activité d’un producteur est celle de savoir dans quelles conditions il lui est techniquement possible de produire en quantités diverses un ou plusieurs biens déterminés. Cela revient à s’interroger sur l’aptitude de ses ressources à réaliser telles ou telles productions. Tout choix rationnel suppose la connaissance des alternatives. Ce que l’économiste doit en savoir porte assez peu sur le détail des processus physiques par lesquels les ressources (inputs) sont transformés en produits (outputs) : il n’est concerné que par les relations entre quantités d’inputs et quantités d’outputs. Une telle relation est décrite au moyen d’un fonction de production : une fonction de production est une relation quantitative entre inputs et outputs, entièrement déterminée par la technologie qui décrit en termes physiques quelle est la quantité d’inputs nécessaire et suffisants pour produire une quantité quelconque d’outputs par unité de temps.

Pour simplifier, nous supposerons qu’il n’existe que deux types d’input : le travail (L) et le capital (K) qui combinés formerons le produit final (Q). Nous pouvons dors et déjà établir une propriété de cette fonction de production qui est la croissance suivant les deux variables capital et travail. Cependant, la relation ainsi définie ne fournit pas seulement des indications sur les quantités mais également sur la relation qui unit les inputs, ce qui permet de constater des phénomènes de substitution dans le domaine de la production.

Considérons en effet un niveau de production Q donné (Q=250) et maintenons le fixe à ce niveau. Il est alors possible de produire cette quantité en combinant 4 unités de capital et 4 de travail ou bien 8 unités de capital et 2 de travail ou encore 1 unité de capital et 16 de travail. Le fait qu’il soit possible d’envisager ces différentes combinaisons de facteurs pour une même quantité produite provient de l’existence de divers procédés techniques pour réaliser un même produit, mais ce passage d’un procédé à un autre implique nécessairement la substitution d’un type d’input à un autre. Pour un niveau donné de production, les substitutions entre facteurs sont résumées dans la notion d’isoquant déduit de la fonction de production.

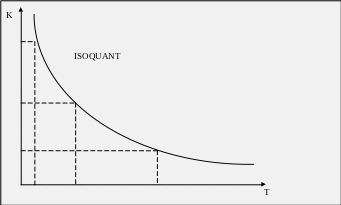
Deux caractéristiques de l’isoquant apparaissent clairement : la courbe est descendante de gauche à droite : cela reflète le fait qu’en cas de diminution de l’un des facteurs, il sera nécessaire d’avoir une augmentation compensatoire de l’autre facteur pour maintenir constant le niveau de production. La courbe est également convexe par rapport à l’origine des axes car plus on renonce à un facteur plus il sera nécessaire d’augmenter la quantité compensatoire de l’autre facteur pour maintenir constant le niveau de la production. La pente de l’isoquant résume ces deux propriétés : d’une part elle est négative, d’autre part, elle décroît en valeur absolue lorsque l’on se déplace de gauche à droite le long de la courbe. Cette pente de l’isoquant est appelée Taux Marginal de Substitution Technique. Le raisonnement peut être répété pour tout autre niveau de la production. Lorsque l’on fait ainsi varier les niveaux de production, on obtient alors une carte d’isoquant. Sur cette carte il est logiquement impossible que deux isoquants se coupent.

Fondamentalement, les producteurs sont appelés à transformer des inputs acquis par eux sur les marchés, en outputs ou produits qu’ils vendent également sur les marchés. L’acquisition des inputs entraîne des dépenses, ou coûts, et les ventes entraînent des recettes. En ce qui concerne les dépenses du producteur, leur étude peut être menée pratiquement en des termes semblables à ceux utilisés pour le consommateur : tandis que le consommateur alloue en fonction de ses préférences son budget à la consommation de divers biens, le producteur répartit sa dépense entre les différents facteurs dont il a besoin, compte tenu des possibilités qu’offrent sa fonction de production.

Le coût total d’un niveau de production donné (CT) est la somme en valeur aux prix du marché, de tous les inputs utilisés par le producteur pour réaliser cette production, pendant une période donnée.

On a, si l’on considère le facteur travail T au prix p_T et le facteur capital au prix p_K :

CT = p_T.T + p_K.K

Ainsi, pour un même coût total, le producteur a le choix entre diverses combinaisons d’input. Ces combinaisons sont alignées le long d’une droite qui est appelée la droite d’isocoût. Le même raisonnement que celui réalisé avec la droite de budget peut être réalisé. L’isocoût exprime un niveau de coût total dans la limite duquel il est possible de substituer du travail à du capital selon un certain rapport. Ce rapport est le TMST et est égal à l’inverse du rapport des prix des facteurs : dK/dT = -(p_T/p_K)

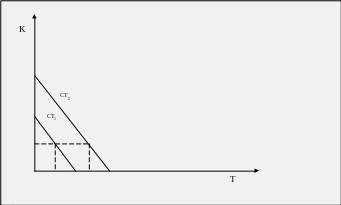
Une dépense globale plus élevée se traduit par un nouvel isocoût, situé à droite et au dessus du premier. Les prix n’ayant pas changé, la pente de la droite reste la même, mais sa position est différente en raison du changement dans le coût total.

Les isoquants font connaître avec précision les quantités de facteurs requis par les diverses techniques de production pour obtenir divers niveau de produit, les isocoûts font savoir, eux, ce que chacune des techniques va coûter au producteur pour tout niveau produit : en traçant isocoûts et isoquants dans un même diagramme, on met alors directement en relation les quantités de facteurs, les coûts et les quantités produites.

Analytiquement, la condition de tangence s’exprime par une relation caractéristique entre les pentes respectives de l’isoquant et de l’isocoût. La pente d’une courbe en un point étant définie par la pente de la tangente en ce point et la tangente se confondant avec l’isocoût au point optimal E, l’optimum est atteint lorsque la pente de l’isoquant est égale à celle de l’isocoût. Au point de coût minimum, les deux rapports sont donc égaux. Economiquement, cette dernière égalité permet de caractériser le choix des facteurs pour une production donnée : ce choix est optimal lorsque le taux marginal de substitution technique entre les facteurs est égal à l’inverse du rapport des prix.

Supposer que le producteur choisit toujours la combinaison des facteurs qui réalise le coût minimum c’est faire une hypothèse sur son comportement : le profit étant la différence entre la totalité des recettes et la totalité des coûts, minimiser ces derniers lorsque la production est fixée, revient à maximiser le profit.