Движение рабочей среды в мэп и захват продуктов эрозии.

При изучении выталкивания рабочей среды газовым пузырем на второй стадии разряда следует учесть, что плотность чистой жидкости _ж  (0,8 ... 1,0) 10³ кг/м³; динамическая вязкость  различных рабочих жидкостей существенно неодинакова (большая вязкость у масла, меньшая у воды, вязкость которой равна 10^-3 Пас) и величина ее с ростом температуры заметно снижается. Кроме того, обогащение рабочих жидкостей продуктами обработки изменяет их свойства.

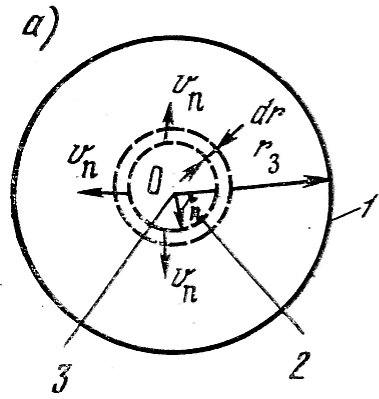
Движение жидкости определяется положением канала разряда относительно контура выходной области МЭП. Ее течение будет строго радиальным (рис. 15, а), когда место пробоя 3 совпадает с центром О упомянутого контура 1, имеющего в плане форму окружности. При радиальном течении жидкости граница газового пузыря 2, находящаяся на расстоянии r_п от центра, движется со скоростью v_n в противном же случае она в плане уже не является окружностью (рис. 15, б), и поэтому вязкая жидкость выталкивается быстрее к ближайшим выходным областям МЭП, а следовательно, газовый пузырь оказывается вытянутым по направлению к ним.

Пусть симметричный пробой произошел в центре МЭП, образованного круглыми торцевыми поверхностями электродов радиусом r₃. Тогда для оценки можно принять, что на выталкивание среды расходуется некоторая доля _в от мгновенной мощности разряда ui, причем для простоты положим ui = const. Расчеты показывают, что при ЭЭО течение в основном ламинарное. Поскольку расходы жидкости для некоторого сечения радиусом r и для границы газового пузыря радиусом r_п одинаковы, то

v = (r_п/r)v_п,

где v_n и v - скорость стенок газового пузыря и средняя скорость жидкости в данном сечении.

Если на расстоянии r от канала разряда выбрать в жидкости кольцо малой ширины dr (см. рис. 15, а), то кинетическая энергия в таком объемесоставит (2adr) _mv²/2. Интегрирование по всему МЭП дает полную кинетическую энергию W_кин, производная которой по времени означает мощность, необходимую для изменения кинетической энергии растекающегося потока:

При течении жидкости через рассматриваемое кольцо затрачивается мощность на преодоление вязкостного трения v2radp_nот, где dp_noт - потери давления на длине dr, согласно формуле Пуазейля равные 3vdt/a². Проведя интегрирование по всему МЭП, получают мощность затрат энергии на преодоление вязкости.

Из закона сохранения энергии вытекает линейное дифференциальное уравнение

_вui = (dW_кин/dt) + (dW_вязк/dt). (42)

Решая уравнение (42) относительно неизвестной величины

(v_nr_n)² = [(dr_п/dt) r_п]2 = [(1/2) dr²_п/dt],

С учетом начальных условии получаем

где r_п.ср - некоторый средний радиус газового пузыря, например, в два раза меньший максимального при t  _и (обычно ln (r₃/r_n.cp)  2,5. Радиус пузыря быстро растет и начальными значениями t_ф.исп и r_ф._исп можно пренебречь. Тогда, обозначив k_r ={4_вuia/[6(lnr_з –lnr_п.ср)]^1/4, получим при t >> t_ф радиус пузыря и скорость его расширения

r_п = k_rt^1/2, (43)

v_n =drп/dt = k_rr^-1/2/2. (44)

Для оценок по формулам (43) и (44) можно принять, что _в  1. Когда r_п = r₃, то МЭП целиком заполняется газом. Чтобы этого не произошло, необходимо с уменьшением г₃ укорачивать длительность разряда пропорционально квадрату радиуса r₃, т. е. площади обработки.

Перепад давлений на упоминавшемся ранее кольце dr определяется повышением давления благодаря меньшей скорости жидкости на внутренней стороне кольца (согласно уравнению Бернулли) и потерями давления вследствие вязкости (по формуле Пуазейля): dp = (_жv²/r) dr - dp_пoт. Проинтегрировав последнее от r₃ до r_п, учтя, что давление в пузыре равно р_п а на выходе из промежутка р_о (причем р_п >>р_о), получим:

(45)

Из уравнения (45) следует, что, действительно, электрический разряд при ЭЭО - это нестационарная дуга высокого давления, поскольку р_п намного превышает атмосферное давление (100 кПа). По аналогии с формулой (15) рассчитывают силу, действующую на электроды, которая оказывается довольно большой:

После прекращения импульса газовый пузырь еще некоторое время медленно расширяется до тех пор, пока давление в нем все еще больше, чем на выходе из промежутка р_о (р_о - обычно атмосферное).

Конечно, наиболее типично такое растекание жидкости (см. рис. 15, б), когда место пробоя 3 несимметрично относительно контура 1. Если в какой-либо точке граница пузыря 2 достигает выхода из МЭП, то здесь газ из пузыря, не встречая сопротивления, устремится во внешнюю среду. Разряды вблизи границы МЭП вызывают довольно непродолжительные течения, а при этом объем вытесняемой из промежутка жидкости невелик. Самые сильные потоки возникают при разрядах в центральных областях МЭП. Объем вытесняемой жидкости в таком случае наибольший и примерно равен максимальному объему газового пузыря.

Захват потоком жидкости инородных включений имеет свои особенности в торцевой (горизонтальной) и вертикальной частях МЭП.

Взвешенные частицы обычно считают сферическими с радиусом r_ч.- Силу G_ч, действующую на такую частицу со стороны потока, молено рассчитать, зная напор жидкости на круг площадью r_ч²,

где v - средняя скорость потока на расстоянии r от оси канала, определяемая по формулам (41) и (44); v_ч - скорость частицы; k_ф - коэффициент формы, который для сферы определяется по экспериментальному соотношению:

k_ф = 10(v-v_ч)^-0,5r_ч^-0,5^0,5_ж^-0,5.

Ускорение частицы под действием силы G_ч согласно закону Ньютона равно G_ч/m_ч, где т_ч - масса частицы, определяемая ее объемом и удельной плотностью материала _ч : т_ч = (4/3) r_ч³_ч.

В итоге получаем уравнение, по которому, зная v, можно найти смещение взвешенной частицы за один разряд

(46)

Сомножитель K_захв = 3,9_ж^0,5^0,5(_ч^-1r_ч^-1,5) определяет степень захвата частиц потоком. В торцевой части МЭП в первую очередь увлекаются взвешенные частицы из вещества с малой плотностью, например, газообразные и мелкие частицы материала электродов.

Общее решение уравнения (46) очень громоздко. Для потока с постоянной скоростью v₀, не зависящей от координаты r, оно имеет вид:

v_ч = v_о – [2/K_захвt - 2v_o^-1/2)]^-2. (47)

Проинтегрировав уравнение (47) но времени, можно найти смещение частицы r_ч в потоке за интервал t. Легкие частицы передвигаются вместе с потоком на расстояние v₀t, для тяжелых частиц, для которых справедливо 2 >>v₀К_захвt, r_ч = 0,5K_захвv_о^1,5t².

Если взять в качестве интервала t длительность разряда _и, т. е. продолжительность расширения газового пузыря, то можно оценить горизонтальное смещение частиц, считая v₀ некоторой скоростью, усредняемой за время импульса. Воспользовавшись формулами (41), (43) и (44), подставив средние значения плотностей жидкости _ж = 10³ кг/м³ и материала заготовки _ч = 10⁴ кг/м³, для крупных частиц находим:

r  410^-4_и²(uia)3/4(r_ч^-1,5r^-1,5^-1/4) (48)

Крупные частицы продуктов эрозии выводятся из МЭП медленнее всех; скорость их удаления из МЭП иногда может не успевать за скоростью их возникновения из лунок *. Происходящее вследствие этого накопление крупных частиц в МЭП ведет к серии пробоев через них. В результате уменьшается объем средних лунок (падает производительность), крупные частицы дробятся разрядами до тех размеров, которые соответствуют большой скорости удаления из МЭП. Данный процесс заканчивается выравниванием обеих скоростей, но при пониженной производительности и более мелких иастицах.

Возможен также захват мелких частиц стенкой набегающего на них газовогo пузыря. Скорее всего, это облегчает развитие последующего электрического пробоя именно вдоль границы газового пузыря. Образовавшиеся, из него более мелкие пузырьки в результате следующих разрядов переходят в вертикальные (боковые) части МЭП, где поднимаются вверх подъемной архимедовой силой, унося с собой налипшие частицы. Тем самым может осуществляться флотационный способ выведения мелких частиц, что имеет основное значение при тех режимах обработки, когда частицы невелики, а кратковременные периоды течения жидкости не обеспечивают вывод их из МЭП.

Удаление частиц из боковой части МЭП - конечный этап их выведения из МЭП вообще. Когда применяют прокачку рабочей среды, то в вертикальной части существует стационарный поток со средней скоростью течения v = (Q + Q_газ)/F_бок, где Q - объемный расход жидкости; Q_газ - объем газа, образующегося в единицу времени в результате разрядов; F_бок - площадь сечения выходной части МЭП.

Для подъема частицы в боковой части МЭП необходимо, чтобы сила G_ч со стороны потока превышала бы силу тяжести, действующую на частицу в жидкости, т. е. согласно выражению (46) скорость v должна быть больше некоторого наименьшего значения v_min = [9,8(1 - _ж/_ч)]^3/2K^-3/2_захв. Подставив в последнее выражение средние величины _ж и _ч, получим:

v_min  180r_ч (49)

Если пренебречь естественным удалением частиц и положить Q_гaз = 0, то знание скорости v_min позволяет установить минимальный расход прокачиваемой жидкости; Q_min = V_minF_бок.

Скорость естественного удаления частиц по мере углубления инструмента в заготовку заметно снижается. Это объясняется двумя причинами: а) ростом площади обрабатываемой поверхности; б) увеличением площади выходного сечения МЭП. При этом искусственная прокачка способствует стабилизации ЭЭО.