12

Квп: Измеритель искажений

1. Цели и задачи исследований

Уровень 1: Изучить параметры гармонических сигналов и способы их оценки, а также изучить органы управления и метрологические характеристики специализированного комплекса виртуальных приборов (КВП). Приобрести практические навыки работы с приборами.

Уровень 2: Применить КВП для исследования спектральных составляющих полигармонического, шумового и комбинированного сигнала. Оценить влияние соотношения амплитуд, частот и начальных фаз компонент спектра на форму и параметры полигармонического сигнала: его пиковых значений и коэффициент амплитуд.

Уровень 3: Изучить и освоить на практике методику поверки измерителя нелинейных искажений (ИНИ) путем определения его основных метрологических характеристик. Выполнить учебную поверку (ИНИ) с помощью образцовых виртуальных приборов.

2. Параметры сигналов и их измерение

Сигналы могут быть непрерывными и модулированными, узкополосными и широкополосными, импульсными и гармоническими, детерминированными и случайными. В измерительных технологиях все большую популярность приобретают полигармонические сигналы, образованные в результате суммирования отдельных гармонических составляющих с заданными амплитудами, частотами и начальными фазами.

Гармонические и полигармонические сигналы характеризуют следующие параметры:

1. Мгновенные значения сигнала в характерных точках наибольшей крутизны, локальных экстремумов и т.д..

2. Амплитудные значения – максимум мгновенных значений.

3. Пиковые значения – максимумы и минимумы полуволн несинусоидальных колебаний (для симметричных полуволн амплитуда равна пику).

4. Размах – сумма пиковых значений.

5. Среднеквадратическое за период напряжение

Для гармонического колебания получим , а для негармонического U_СК определяется амплитудами гармоник (U_i) и постоянной составляющей (U_o) сигнала:

Для различных законов изменения напряжения связь амплитудного значения и среднеквадратического определяется коэффициентом амплитуды:

Для гармонического - К_аг=1,41;

Для пилообразного - К_ап=1,73;

Для меандра - К_ам=1,00.

Искажения гармонического сигнала оценивают коэффициентом гармоник (К_Г), который также называют коэффициентом несинусоидальности или коэффициентом нелинейных искажений (КНИ). КНИ показывает вес высших гармонических составляющих в спектре сигнала по отношению к первой гармонике в относительном масштабе или в процентах:

Методы измерения КНИ

1. Спектральные – на базе селективных приборов (АС, СВ).

2. Квазиспектральные – на базе подавления первой гармоники (ИНИ).

Спектральный метод с применением АС сложен аппаратно, а с применением СВ требует длительных измерений и вычислений, поэтому в автономных приборах (подгруппа С6) широкое распространение получил квазиспектральный метод, который прост аппаратно и отличается от спектрального тем, что в выражении для К_Г другой знаменатель:

, где .

Подобная замена упрощает схему прибора и алгоритм его работы, но вносит методическую погрешность в уравнение измерения, хотя заметные отличия результатов проявляются только при К_Г >10 %.

Спектр любого периодического сигнала является дискретным или линейчатым. В общем случае периодический сигнал содержит постоянную составляющую и набор гармонических колебаний с частотами _=K_, K=1,2,3…, кратными основной частоте _.

Например, сигнал пилообразной формы может быть представлен суперпозицией бесконечного количества синусоидальных сигналов, частоты которых кратны основной частоте. Амплитуда и мощность этих синусоид уменьшаются с увеличением их частоты. По мере добавления каждой гармоники, форма сигнала становится более похожей на идеальную. Ряд Фурье пилообразного сигнала имеет вид:

.

Идеальный сигнал прямоугольной формы включает в себя бесконечное количество нечетных гармоник. В таком случае ряд Фурье выглядит как:

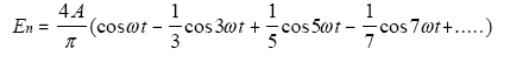
Так как амплитуда гармоник высоких порядков во много раз меньше амплитуды основной частоты, то, как правило, вычисляют ограниченное число гармоник.

В вычислительных ИНИ применяются методы обработки дискретизированных сигналов в частотной области. В частности, в виртуальном ИНИ, используемом в лабораторных исследованиях, реализован принцип оценки К_Г на основе алгоритма БПФ.