1)Кинематика поступательного движения материальной точки.

Кинематика изучает движение тел, не рассматривая причины, которые это движение обусловливают.

Материальная точка — тело, обладающее массой, размерами которого в данной задаче можно пренебречь.

Поступательное движение — это движение, при котором любая прямая, жестко связанная с движущимся телом, остается параллельной своему первоначальному положению.

Система отсчета — совокупность системы координат и часов.

Кинематические уравнения движения материальной точки

В общем случае ее движение определяется скалярными уравнениями x=x(t), y=y(t),z=z{t)

векторному уравнению r = r(t).

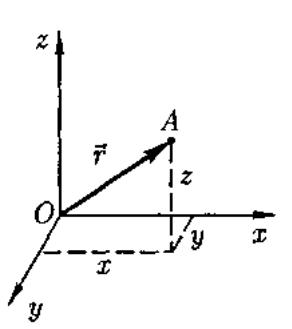
В декартовой системе координат, используемой наиболее часто, положение точки А в данный момент времени по отношению к этой системе характеризуется тремя координатами х, у и z или радиусом-вектором г, проведенным из начала системы координат в данную точку

Движение материальной точки будет описано полностью, если известно ее положение в любой момент времени относительно выбранной системы отсчета. Полное описание движения сводится к нахождению трех координат: x = x(t); y = y(t); z = z(t); или к нахождению векторной функции r = r(t)

Число независимых величин, полностью определяющих положение точки в пространстве, называется числом степеней свободы.

Траектория — линия, описываемая в пространстве движущейся точкой

2)Путь, перемещение, скорость, ускорение.

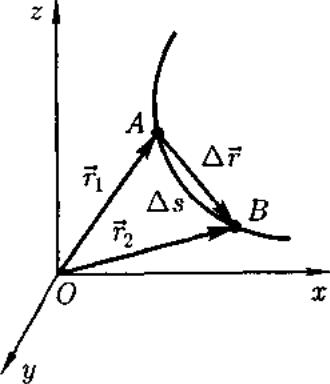
Длина участка траектории А В, пройденного материальной точкой с момента начала отсчета времени, называется длиной пути (дельта)S является скалярной функцией времени: As = As(t).

Вектор (дельта)г = г2 — Г1 проведенный из начального положения движущейся точки в положение ее в данный момент времени (приращение радиуса-вектора точки за рассматриваемый промежуток времени), называется перемещением.

Скорость – векторная величина, быстрота движения.

Скорость- векторная физическая величина, служащая для характеристики направления и быстроты движения точки в механике. Средней скоростью точки в промежутке времени от

до называется вектор , равный отношению приращения радиуса-вектора точки за этот промежуток времени к его продолжительности :

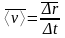
Средняя скорость направлена так же, как вектор перемещения , то есть вдоль хорды, стягивающей соответствующий участок траектории точки.

Скоростью точки в момент времени называется вектор 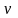, равный первой производной по времени от радиуса-вектора этой точки:

.

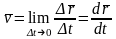
Вектор можно разложить по базису , то есть на три составляющие по осям прямоугольной декартовой системы координат.

.

.

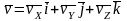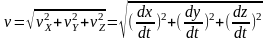Вектором средней скорости (v) называется отношение приращения (дельта)г радиуса-вектора точки к промежутку времени At:

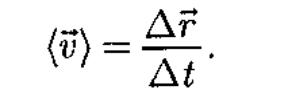Направление вектора средней скорости совпадает с направлением (дельта)г. При неограниченном уменьшении At средняя скорость стремится к предельному значению, которое называется мгновенной скоростью v:

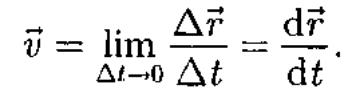
Ускорение – это величина, показывающая, как изменяется скорость за одну секунду.

Ускорение.

Ускорение- векторная физическая величина, характеризующая быстроту изменения скорости .

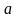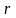Ускорением называется вектор , равный первой производной по времени от скорости этой точки. Ускорение точки также равно второй производной по времени от радиуса-вектора этой точки:

.

Разложение ускорения точки по базису , то есть на составляющие по осям прямоугольной декартовой системы координат, имеет вид:

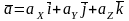, где

, , .

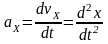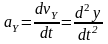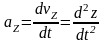Здесь 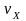, ,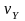 - компоненты скорости точки, а 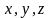- координаты точки в рассматриваемый момент времени.

За единицу скорости принимают скорость такого равномерного прямолинейного движения, при котором тело за одну секунду перемещается на один метр.

Ускорение – это величина, показывающая, как изменяется скорость за одну секунду.

Равномерное прямолинейное движение

Равномерным прямолинейным движением называется такое прямолинейное движение, при котором материальная точка (тело) движется по прямой и в любые равные промежутки времени совершает одинаковые перемещения.

Вектор скорости равномерного прямолинейного движения материальной точки направлен вдоль ее траектории в сторону движения. Вектор скорости при равномерном прямолинейном движении равен вектору перемещения за любой промежуток времени, поделенному на этот промежуток времени:

Примем линию, по которой движется материальная точка, за ось координат ОХ, причем за положительное направление оси выберем направление движения точки. Тогда, спроецировав векторы r и v, на эту ось, для проекций ∆rx = |∆r| и ∆vx = |∆v| этих векторов мы можем записать:

, отсюда получаем уравнение равномерного движения:

Т.к. при равномерном прямолинейном движении S = |∆r|, можем записать: Sx = Vx · t. Тогда для координаты тела в любой момент времени имеем:

где - координата тела в начальный момент t = 0.

Равнопеременное прямолинейное движение

Равнопеременным называется движение, при котором скорость тела (материальной точки) за любые равные промежутки времени изменяется одинаково, т.е. на равные величины. Это движение может быть равноускоренным и равнозамедленным.

Если направление ускорения а совпадает с направлением скорости V точки, движение называется равноускоренным. Если направление векторов а и V противоположны, движение называется равнозамедленным.

При равнопеременном прямолинейном движении ускорение остается постоянным и по модулю и по направлению (а = const). При этом среднее ускорение а_ср равно мгновенному ускорению а вдоль траектории точки. Нормальное ускорение при этом отсутствует (а_n=0).

Изменение скорости ∆v = v - v₀ в течении промежутка времени ∆t = t - t₀ при равнопеременном прямолинейном движении равно: ∆v = a·∆t, или v - v₀ = a·(t - t₀). Если в момент начала отсчета времени (t₀) скорость точки равна v₀ (начальная скорость) и ускорение а известно, то скорость v в произвольный момент времени t: v = v₀ + a·t. Проекция вектора скорости на ось ОХ связана с соответствующими проекциями векторов начальной скорости и ускорения уравнением: v_х = v_0х ± a_х·t. Аналогично записываются уравнения для проекций вектора скорости на другие координатные оси.

Вектор перемещения ∆r точки за промежуток времени ∆t = t - t₀ при равнопеременном прямолинейном движении с начальной скоростью v₀ и ускорением а равен:

а его проекция на ось ОХ (или перемещение точки вдоль соответствующей оси координат) при t₀ = 0 равна:

Путь S_x, пройденный точкой за промежуток времени ∆t = t - t₀ в равнопеременном прямолинейном движении с начальной скоростью v₀ и ускорением а, при t₀ = 0 равен:

Так как координата тела равна х = х₀ + S, то уравнение движения тела имеет вид:

Возможно так же при решении задач использовать формулу: