5.4. Выбор оптимальной величины и размещения оперативного резерва мощности в оэс

Надежность электроснабжения потребителей в ОЭС определяется величинами установленных мощностей агрегатов в отдельных узлах (подсистемах), аварийностью агрегатов, а также параметрами ЛЭП и их аварийностью. Для обеспечения оптимальной надежности ОЭС необходимо так выбрать установленные мощности агрегатов в каждой из подсистем и пропускные способности межсистемных связей, чтобы было выполнено условие минимума приведенных затрат (целевой функции), включающих и математическое ожидание ущерба.

,

при условии .

Здесь - дополнительные капиталовложения: :в резервные агрегаты мощностью размещаемые в -м узле;

- издержки производства, связанные с использованием резерва в -м узле;

- математическое ожидание ущерба у потребителей в ОЭС;

- число узлов в ОЭС;

- переток мощности по ЛЭП при дефиците мощности в -м или -м узле;

- пропускная способность -й ЛЭП.

При определении резервов мощности в ОЭС примем, что маневренные потоки мощности, возникающие при дефиците мощности в узле, передаются только по ЛЭП, непосредственно примыкающим к дефицитному узлу (рис. 24).

Рис. 24. Модель ОЭС для определения дефицита мощности

Если при определении резерва мощности в концентрированной ЭЭС минимизируемые затраты являются нелинейной функцией одной дискретно изменяющейся переменной, то при оптимизации резерва мощности в ОЭС затраты являются нелинейной функцией L дискретных переменных (L - число узлов). Для минимизации функций такого вида, помимо перебора всех вариантов, можно использовать метод динамического программирования, метод дискретного

покоординатного спуска. Минимизация методом покоординатного спуска заключается в последовательной минимизации функции одной переменной при фиксированном значении остальных.

Варианты резервирования в -м узле представим в виде множества дискретных значений, принимаемых -й переменной

где - число вариантов резервирования: в -м узле.

Всю совокупность возможных значений переменных представим таблицей возможных дискретных значений оптимизируемых параметров

.

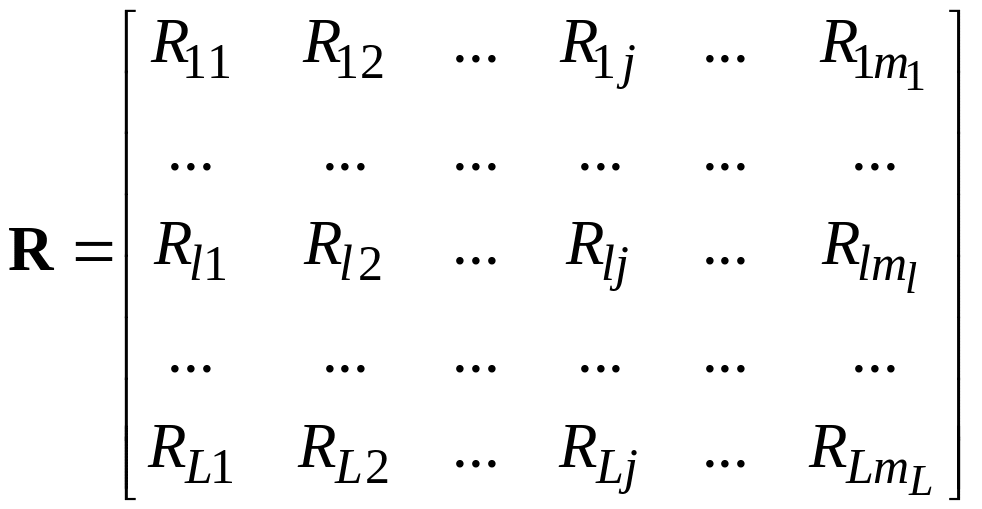Процесс спуска по заданной совокупности L переменных является одним циклом расчета. На первом цикле расчета спуск по -й координате начинается с выявления той величины или , при которой значение затрат меньше. Затем рассматривается значение переменной ближайшее к предыдущему. Поскольку функция выпукла вниз, то последовательный просмотр значений переменной проводится до выполнения: условия

,

где определена при фиксированном значении всех переменных кроме -й. Спуск по -й координате заканчивается на значении которое фиксируется при движении по другим координатам. Процесс спуска заканчивается в точке тогда, когда дополнительный цикл расчета не дает снижения затрат.

Для расчета ущерба у потребителей и топливных затрат, входящих в целевую функцию, необходимо определить математическое ожидание недоотпуска электроэнергии в ОЭС при различных вариантах размещения резерва мощности. В ОЭС, состоящей из 6-8 энергетических узлов, вероятность одновременного дефицита в нескольких узлах очень мала и такие события можно не рассматривать. Тогда математическое ожидание недоотпуска электроэнергии и ущерба в ОЭС определим путем последовательного перебора состояний с дефицитом мощности в каждом узле объединения.

Для того, чтобы учесть ограничения на перетоки мощности по ЛЭП и аварийные отключения ЛЭП, необходимо рассматривать изменения нагрузок узлов по характерным суточным графикам нагрузки. Суточные графики нагрузок узлов представим: в виде ступенчатых графиков снижения мощности относительно максимума нагрузки (рис. 25).

Рис. 25. График нагрузки узла

Для учета аварийного отключения: агрегатов и ошибок: прогнозирования нагрузки воспользуемся рядами вероятностей дефицитов и избытков мощностей, рассчитанными для моментов максимумов нагрузок каждого узла. Обозначим через ( ) и ( ) соответственно ряды вероятностей дефицитов и избытков мощности при максимальной нагрузке системы. Члены рядов и найдем по формулам:

где - вероятность дефицита мощности в размере при нагрузке ;

- вероятность из6ытка мощности - при нагрузке ;

- вероятность отключения агрегатов суммарной мощностью ;

М - наибольший номер члена ряда вероятностей аварийного отключения агрегатов.

В некотором интервале t суточного графика (рис. 25) в i-м узле может 6ыть дефицит мощности в размере

с вероятностью или избыток мощности в размере

с вероятностью . Здесь - вероятность дефицита мощности в i-м узле из-за отключений агрегатов и отклонений нагрузки от максимальной в размере МВт; - вероятность избытка мощности в i-м узле в размере - ; - снижение нагрузки по отношению к максимальной в интервале t суточного графика; - резерв мощности в i-м узле.

Дефициты мощности в ОЭС определяются последовательно для всех интервалов t суточного графика нагрузки. Если дефицитный узел i имеет связь только с одним бездефицитным узлом j (рис. 24), то вероятность дефицита мощности в ОЭС в t -м интервале времени в размере равна

,

где - вероятность отключения ЛЭП, связывающей -й и -й узлы;

- интегральная вероятность из6ытка мощности в -м узле.

= + + +…

- наименьшее из двух чисел: пропускной способности ЛЭП i- и наибольшего избытка мощности в j–м узле:

.

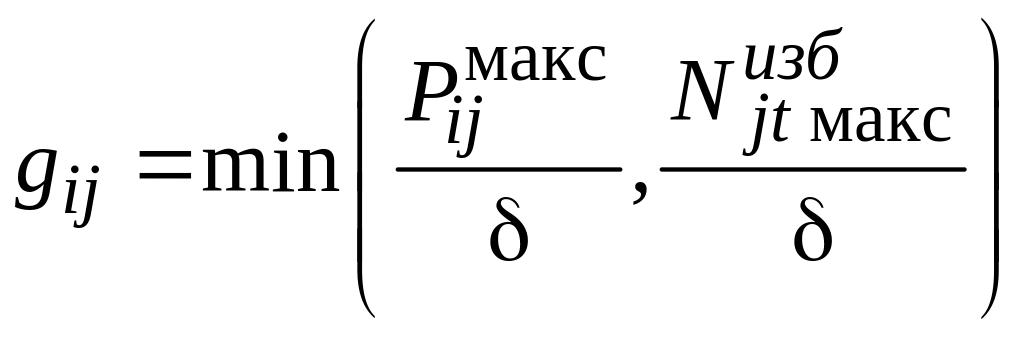Математические ожидания недоотпуска электроэнергии и ущерба в t-м интервале времени в ОЭС при дефиците мощности в i-м узле определяются по следующим выражениям:

,

,

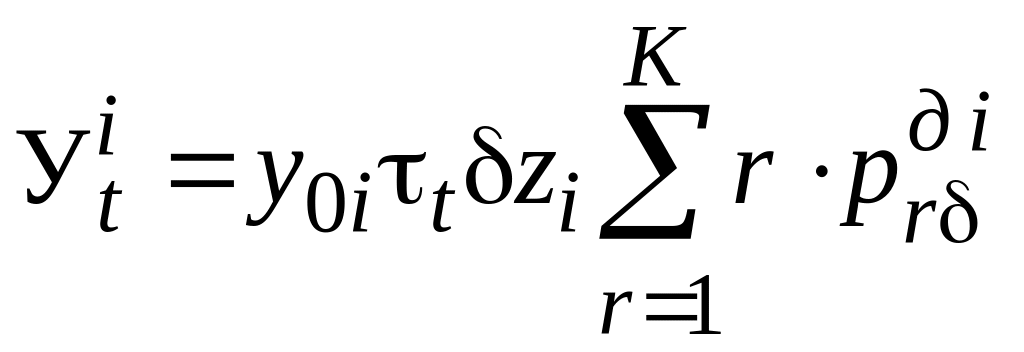где - длительность t-гo интервала времени;

- вероятность бездефицитного состояния в узлах, не связанных непосредственно с i-м узлом; .

- максимальная ступень дефицита мощности в i-м узле;

- удельный ущерб от недоотпуска электроэнергии в i-м узле.

,

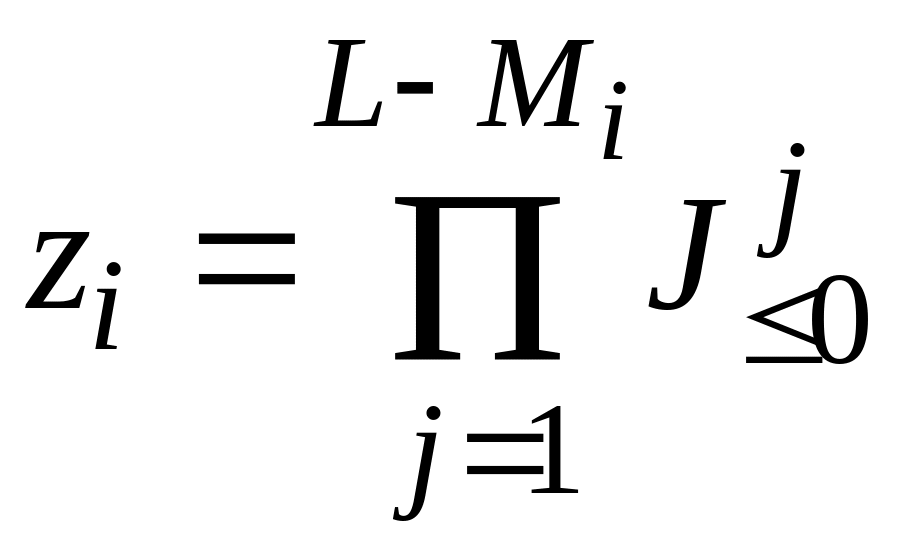где L - число узлов, входящих в объединение;

- число узлов, непосредственно связанных с i-м.

Суммируя и по всем узлам вначале в разрезе суток, а затем года, определим математические ожидания недоотпуска. электроэнергии и ущерба за год, которые используются при расчете затрат по ОЭС:

,

,

Здесь Н число характерных суточных графиков нагрузки в году; - число суток работы по h-му графику нагрузки; - число интервалов в h -м графике.