Показатели надежности электроснабжения
Степень выполнения функций системы характеризуется показателями надежности. В зависимости от исследуемых функций системы рассматривают следующие виды отказов:
1. Частичная или полная потеря работоспособности какого-либо элемента системы независимо от того отражается это на электроснабжении потребителей или нет.
2. Ограничение электроснабжения потребителей системы (района), вызываемое повреждением. элементов или непредвиденным ростом нагрузки.
3. Недопустимое отклонение напряжения: из-за повреждений или роста нагрузки.
4. Нарушение статической или динамической устойчивости.
Используют следующие показатели надежности:
А.
Показатель, связанный с частотой отказов:
параметр потока отказов
- математическое ожидание числа отказов
в единицу времени.
Б. Показатели, связанные с продолжительностью безотказной
работы и отказов:
1. Средняя
продолжительность безотказной работы
(наработка на отказ) -
.
Функция: распределения вероятностей продолжительности безотказной работы
.Функция распределения вероятностей продолжительности откaза
.
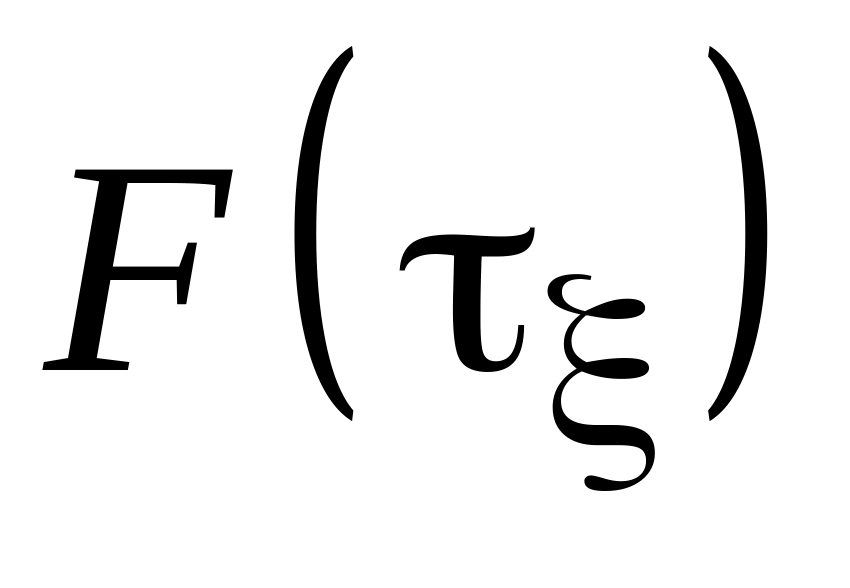4. Средняя
продолжительность отказа (среднее время
восстановления) -
или
.
5. Математическое ожидание случайной суммарной продолжительности безотказной работы за расчетный период, отнесенное к продолжительности этого периода (вероятность работоспособности) p.
6. Математическое ожидание случайной суммарной продолжительности отказов за расчетный период, отнесенное к продолжительности этого периода (вероятность нахождения системы в состоянии отказа) q.
В. Показатели, интегрально учитывающие частоту, продолжительность и глубину отказов:
1.
Функция распределения вероятностей
недоотпyска электроэнергии потребителям
в течение расчетного периода -
.
2.
Среднее значение математического
ожидания недоотпyска электроэнергии
потребителям в течение расчетного
периода -
.
3.
Относительное удовлетворение потребителей
электроэнергией в течение расчетного
периода
(
W
– необходимое количество энергии).
4. Среднее значение математического ожидания ущерба потребителей от недоотпуска электроэнергии и понижения ее качества в течение расчетного периода - У.
Применение тех или иных показателей надежности определяется содержанием решаемых задач и проектным или эксплуатационным уровнем решения.
1.
При определении величины и размещения
резервов генерирующей мощности при
проектировании ЭЭС используют
или У.
2. При распределении резервов генерирующей мощности в условиях эксплуатации ЭЭС - р и .
3. При расчете надежности электроснабжения (электрической сети) на проектных уровнях - p, q и .
4. При расчете надежности электроснабжения (электрической сети) при эксплуатации - , , , и др.
1.3. Методы расчета показателей надежности
Показатели надежности определяют, если известны:
- расчетная схема ЭЭС;
- состав работающего, ремонтируемого оборудования, резервного оборудования;
- показатели надежности элементов расчетной схемы;
- значения нагрузок потре6ителей, представленных в расчетной схеме;
- энергоресурсы.
В зависимости от рассматриваемой расчетной схемы различают ЭЭС со слабыми и сильными внутренними связями. ЭЭС со слабыми связями - это система, у которой пропускная способность связей (определяемая статической или динамической устойчивостью, нагревом проводов и т.п.) ограничивает использование мощности электростанций для питания нагрузки в некоторых режимах. В таких: ЭЭС возможно нарушение устойчивости. При расчете надежности учитывают отказы и генерирующего и сетевого оборудования. ЭЭС с сильными связями - система, у :которой пропускная способность не ограничивает использования мощности электростанций в любой точке системы при любых режимах. При расчете надежности учитывают отказы только генерирующего оборудования. Это - концентрированная ЭЭС.
Поведение исследуемой системы во времени можно представить как случайный процесс, который определяется случайным характером отказов элементов, изменением нагрузки и т.п. (рис. 1). В зависимости от различных предположений о характере случайного процесса можно использовать тот или иной математический аппарат для расчета показателей надежности. Для неизменного режима ЭЭС и, если частота отказов постоянна, а время восстановления определяется экспоненциальным законом распределения, используют аппарат марковских случайных процессов.
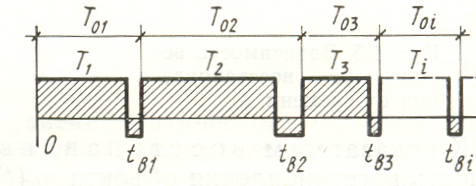
Рис.1 Поток отказов и восстановлений
Если определяют средние значения показателей надежности (p, q, , У),то задача может быть решена на уровне случайных событий с использованием теорем теории вероятностей. В общем случае, не накладывая никаких ограничений на характер случайного процесса, используют метод статистических испытаний.