Аnоvа с повторными измерениями
АNОVА с повторными измерениями применяется, когда, по крайней мере, один из факторов изменяется по внутригрупповому плану, то есть различным градациям этого фактора соответствует одна и та же выборка объектов (испытуемых). Соответственно, в модели АNОVА с повторными измерениями выделяются внутригрупповые и межгрупповые факторы.
Различают одномерные и многомерные модели ANOVA с повторными измерениями.
Одномерная модель предполагает, что каждому уровню внутригруппового фактора соответствует повторное измерение одной и той же зависимой переменной (то есть эти измерения положительно коррелируют).
Многомерная модель свободна от допущения о корреляции измерений зависимой переменной.
Для начала рассмотрим задачу, в которой исследуется влияние двух факторов на одну и ту же выборку.
Задача 11.33. В выборке курсантов военного училища (юноши в возрасте 18–20 лет) измерялась способность к удержанию физического волевого усилия на динамометре. В первый день эксперимента у них, наряду с другими показателями, измерялась мышечная сила каждой из рук. На второй день эксперимента им предлагалось выдерживать на динамометре мышечное усилие, равное ½ максимальной мышечной силы данной руки. На третий день эксперимента испытуемым предлагалось проделать то же самое в парном соревновании на глазах у всей группы. Пары соревнующихся были подобраны таким образом, чтобы сила обеих рук у них примерно совпадала. Результаты эксперимента представлены в таблице (Таблица 11 .9).
Таблица 11.9
Длительность удержания усилия (сек\10) на динамометре правой и левой руками в разных условиях измерения
№ |
Вне группы |
В группе |
||
Правая рука |
Левая рука |
Правая рука |
Левая рука |
|
1 |
11 |
10 |
15 |
10 |
2 |
13 |
11 |
14 |
10 |
3 |
12 |
8 |
8 |
5 |
4 |
9 |
10 |
7 |
8 |
Зависимая переменная — длительность удержания физического волевого усилия. Фактор А — соревнование в группе (две градации): 1 — вне группы (наедине с экспериментатором); 2 — в группе соревнующихся. Фактор В — рука испытуемого (две градации): 1 — правая; 2 — левая.
Проверяются гипотезы (H1):
Фактор соревнования в группе влияет на продолжительность волевого усилия.
Правая рука более «социальна» (правая рука в меньшей степени «сдаётся» под влиянием усталости в ситуации соревнования в группе, чем вне группы).
Применяется одномерная модель двухфакторного ANOVA с повторениями.
Одномерная модель двухфакторного anova с повторениями в пакете Анализ данных
Д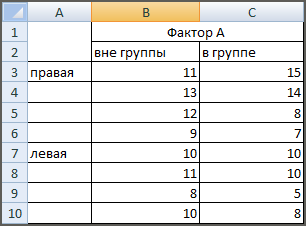
ля
применения двухфакторного анализа в
MS
Excel
необходимо ввести исходные данные так
как указано на рисунке.
Выбрать пункт меню Сервис \ Анализ данных… \ Двухфакторный дисперсионный анализ с повторениями.
В поле Входной интервал ввести ссылку на массив, содержащий данные измерений (прямоугольный диапазон A2:C10).
В поле Число строк для выборки ввести объём выборки (4).
Выделить мышью выходной интервал, предварительно щёлкнув по радиокнопке Выходной интервал. Нажать ОК.
Таблица 11 .10 показывает основной результат работы двухфакторного ANOVA c повторениями. Из таблицы видно, что гипотеза о влиянии фактора соревнования отвергается (p-значение для столбцов больше 0,05). Гипотеза о «социальности» правой руки также отвергается (p-значение для взаимодействия больше 0,05).
Таблица 11.10
Дисперсионный анализ |
|
|
|
|
|
|
Источник вариации |
SS |
df |
MS |
F |
P-Значение |
F критическое |
Выборка |
18,0625 |
1 |
18,0625 |
2,700935 |
0,126214481 |
4,747225336 |
Столбцы |
3,0625 |
1 |
3,0625 |
0,457944 |
0,511420432 |
4,747225336 |
Взаимодействие |
1,5625 |
1 |
1,5625 |
0,233645 |
0,637533939 |
4,747225336 |
Внутри |
80,25 |
12 |
6,6875 |
|
|
|
|
|
|
|
|
|
|
Итого |
102,9375 |
15 |
|
|
|
|