МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РФ ФГБОУ ВПО «БАШКИРСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ» ЗАУРАЛЬСКИЙ ФИЛИАЛ

Экзаменационный билет №1 Кафедра: ФИЗИКИ, МАТЕМАТИКИ И ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ Дисциплина: Теоретические основы электротехники Направления «Агроинженерия» II курс

УТВЕРЖДЕНО НА ЗАСЕДАНИИ КАФЕДРЫ « » 2012 г. Зав. кафедрой ____________Музафаров С. М.

Элементы электрических цепей.

Способы представления периодических несинусоидальных величин.

Задача.

1. Электрическая цепь представляет собой совокупность источников электрической энергии, приёмников (потребителей) и соединяющих их проводников, по которым электрическая энергия передаётся от источников потребителям.

Все элементы электрической цепи условно можно разделить на активные и пассивные. Активным называется элемент, содержащий в своей структуре источник электрической энергии. К пассивным относятся элементы, в которых рассеивается (резисторы) или накапливается (катушка индуктивности и конденсаторы) энергия. К основным характеристикам элементов цепи относятся их вольт-амперные, вебер-амперные и кулон-вольтные характеристики, описываемые дифференциальными или (и) алгебраическими уравнениями. Если элементы описываются линейными дифференциальными или алгебраическими уравнениями, то они называются линейными, в противном случае они относятся к классу нелинейных. Строго говоря, все элементы являются нелинейными. Возможность рассмотрения их как линейных, что существенно упрощает математическое описание и анализ процессов, определяется границами изменения характеризующих их переменных и их частот. Коэффициенты, связывающие переменные, их производные и интегралы в этих уравнениях, называются параметрами элемента.

Если параметры элемента не являются функциями пространственных координат, определяющих его геометрические размеры, то он называется элементом с сосредоточенными параметрами. Если элемент описывается уравнениями, в которые входят пространственные переменные, то он относится к классу элементов с распределенными параметрами. Классическим примером последних является линия передачи электроэнергии (длинная линия).

Цепи, содержащие только линейные элементы, называются линейными. Наличие в схеме хотя бы одного нелинейного элемента относит ее к классу нелинейных.

Рассмотрим пассивные элементы цепи, их основные характеристики и параметры.

1. Резистивный элемент (резистор)

Условное графическое изображение резистора приведено на рис. 1,а. Резистор – это пассивный элемент, характеризующийся резистивным сопротивлением. Последнее определяется геометрическими размерами тела и свойствами материала: удельным сопротивлением  (Ом м) или обратной величиной – удельной проводимостью (См/м).

В простейшем случае проводника длиной и сечением S его сопротивление определяется выражением

.

В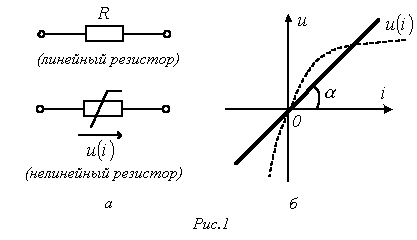 общем случае определение сопротивления связано с расчетом поля в проводящей среде, разделяющей два электрода.

Основной характеристикой резистивного элемента является зависимость (или ), называемая вольт-амперной характеристикой (ВАХ). Если зависимость представляет собой прямую линию, проходящую через начало координат (см.рис. 1,б), то резистор называется линейным и описывается соотношением

или

,

где - проводимость. При этом R=const.

Нелинейный резистивный элемент, ВАХ которого нелинейна (рис. 1,б), как будет показано в блоке лекций, посвященных нелинейным цепям, характеризуется несколькими параметрами. В частности безынерционному резистору ставятся в соответствие статическое и дифференциальное 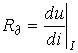сопротивления.

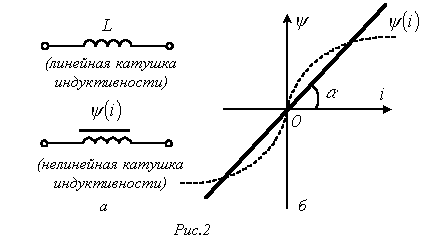
2. Индуктивный элемент (катушка индуктивности)

Условное графическое изображение катушки индуктивности приведено на рис. 2,а. Катушка – это пассивный элемент, характеризующийся индуктивностью. Для расчета индуктивности катушки необходимо рассчитать созданное ею магнитное поле.

Индуктивность определяется отношением потокосцепления к току, протекающему по виткам катушки,

.

В свою очередь потокосцепление равно сумме произведений потока, пронизывающего витки, на число этих витков , где .

Основной характеристикой катушки индуктивности является зависимость , называемая вебер-амперной характеристикой. Для линейных катушек индуктивности зависимость представляет собой прямую линию, проходящую через начало координат (см. рис. 2,б); при этом

.

Нелинейные свойства катушки индуктивности (см. кривую на рис. 2,б) определяет наличие у нее сердечника из ферромагнитного материала, для которого зависимость магнитной индукции от напряженности поля нелинейна. Без учета явления магнитного гистерезиса нелинейная катушка характеризуется статической и дифференциальной 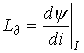индуктивностями.

3. Емкостный элемент (конденсатор)

Условное графическое изображение конденсатора приведено на рис. 3,а.

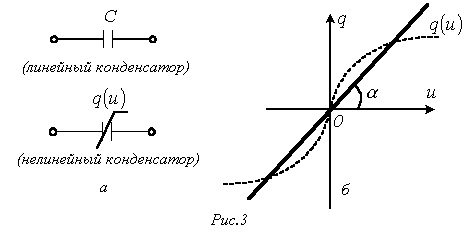
Конденсатор – это пассивный элемент, характеризующийся емкостью. Для расчета последней необходимо рассчитать электрическое поле в конденсаторе. Емкость определяется отношением заряда q на обкладках конденсатора к напряжению u между ними

и зависит от геометрии обкладок и свойств диэлектрика, находящегося между ними. Большинство диэлектриков, используемых на практике, линейны, т.е. у них относительная диэлектрическая проницаемость =const. В этом случае зависимость представляет собой прямую линию, проходящую через начало координат, (см. рис. 3,б) и

.

У нелинейных диэлектриков (сегнетоэлектриков) диэлектрическая проницаемость является функцией напряженности поля, что обусловливает нелинейность зависимости (рис. 3,б). В этом случае без учета явления электрического гистерезиса нелинейный конденсатор характеризуется статической и дифференциальной 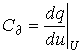емкостями.

2. Способы представления периодических несинусоидальных величин.

Периодические несинусоидальные величины могут быть представлены временными диаграммами, тригонометрическим рядом Фурье, а также эквивалентными синусоидами. Наиболее наглядными, дающими полное представление о несинусоидальной величине являются временные диаграммы, т. е. графики зависимости мгновенных значений от времени (рис. 4.1 - рис. 4.2)

Несинусоидальные ЭДС, токи и напряжения, с которыми приходится встречаться в электротехнике и промышленной электронике, являются периодическими функциями, удовлетворяющими условиям Дирихле и, следовательно, могут быть представлены тригонометрическим рядом Фурье:

Тригонометрический ряд может быть представлен как в виде суммы синусов (синусный ряд), так и суммы косинусов (косинусный ряд) гармонических составляющих.

В зависимости от характера реальной кривой f(ωt) тригонометрический ряд может не содержать постоянной составляющей, четных или нечетных высших гармоник, а также начальных фаз. Например, тригонометрические ряды Фурье некоторых несинусоидальных напряжений имеют вид:

напряжение на нагрузке при однополупериодном выпрямлении (см. рис. 4.1а)

напряжение на нагрузке при двухполупериодном выпрямлении (см. рис. 4.1б)

напряжение треугольной формы (см. рис. 4.2а)

напряжение прямоугольной формы (см. рис. 4.2б)

В практических расчетах цепей с несинусоидальными ЭДС, токами и напряжениями их мгновенные значения приближенно отображают конечным рядом Фурье (3—7 членов ряда). Число членов ряда определяется необходимой точностью расчета.

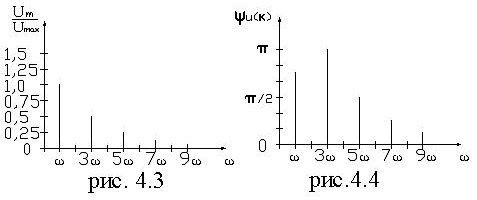
Характеристика несинусоидальных величин, представленных рядом Фурье, может быть осуществлена графически с помощью диаграмм амплитудно-частотного (рис. 4.3), фазо - частотного (рис. 4.4) спектров.

Данные диаграммы характеризуют форму несинусоидальных кривых, причем первая диаграмма показывает спектральный состав по амплитудам, т. е. представляет зависимость амплитуд гармоник в относительных единицах от частоты, вторая диаграмма выражает зависимость начальных фаз гармоник от частоты.

Периодические несинусоидальные ЭДС, напряжения и токи могут быть представлены так же эквивалентными синусоидами.

3. Задача.

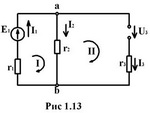
Записать уравнения по законам Кирхгофа для расчета токов цепи, представленной на рис.1.13.

МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РФ ФГБОУ ВПО «БАШКИРСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ» ЗАУРАЛЬСКИЙ ФИЛИАЛ

Экзаменационный билет №2 Кафедра: ФИЗИКИ, МАТЕМАТИКИ И ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ Дисциплина: Теоретические основы электротехники Направления «Агроинженерия» II курс

УТВЕРЖДЕНО НА ЗАСЕДАНИИ КАФЕДРЫ « » 2012 г. Зав. кафедрой ____________Музафаров С. М.

Схемы замещения источников электрической энергии.

Влияние резистивного, индуктивного и емкостного элементов цепи при несинусоидальном токе на форму кривой тока.

Задача.

1. Схемы замещения источников электрической энергии

Свойства источника электрической энергии описываются ВАХ , называемой внешней характеристикой источника. Далее в этом разделе для упрощения анализа и математического описания будут рассматриваться источники постоянного напряжения (тока). Однако все полученные при этом закономерности, понятия и эквивалентные схемы в полной мере распространяются на источники переменного тока. ВАХ источника может быть определена экспериментально на основе схемы, представленной на рис. 4,а. Здесь вольтметр V измеряет напряжение на зажимах 1-2 источника И, а амперметр А – потребляемый от него ток I, величина которого может изменяться с помощью переменного нагрузочного резистора (реостата) R_Н.

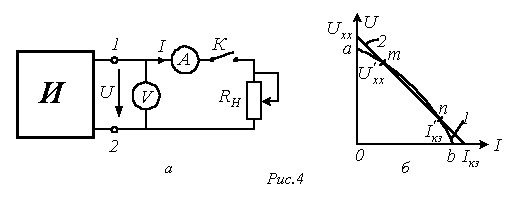
В общем случае ВАХ источника является нелинейной (кривая 1 на рис. 4,б). Она имеет две характерные точки, которые соответствуют:

а – режиму холостого хода ;

б – режиму короткого замыкания .

Для большинства источников режим короткого замыкания (иногда холостого хода) является недопустимым. Токи и напряжения источника обычно могут изменяться в определенных пределах, ограниченных сверху значениями, соответствующими номинальному режиму (режиму, при котором изготовитель гарантирует наилучшие условия его эксплуатации в отношении экономичности и долговечности срока службы). Это позволяет в ряде случаев для упрощения расчетов аппроксимировать нелинейную ВАХ на рабочем участке m-n (см. рис. 4,б) прямой, положение которой определяется рабочими интервалами изменения напряжения и тока. Следует отметить, что многие источники (гальванические элементы, аккумуляторы) имеют линейные ВАХ.

Прямая 2 на рис. 4,б описывается линейным уравнением

,

(1)

где - напряжение на зажимах источника при отключенной нагрузке (разомкнутом ключе К в схеме на рис. 4,а); - внутреннее сопротивление источника.

Уравнение (1) позволяет составить последовательную схему замещения источника (см. рис. 5,а). На этой схеме символом Е обозначен элемент, называемый идеальным источником ЭДС. Напряжение на зажимах этого элемента не зависит от тока источника, следовательно, ему соответствует ВАХ на рис. 5,б. На основании (1) у такого источника . Отметим, что направления ЭДС и напряжения на зажимах источника противоположны.

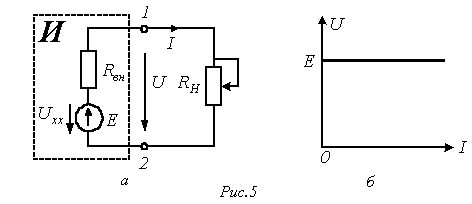
Если ВАХ источника линейна, то для определения параметров его схемы замещения необходимо провести замеры напряжения и тока для двух любых режимов его работы.

Существует также параллельная схема замещения источника. Для ее описания разделим левую и правую части соотношения (1) на . В результате получим

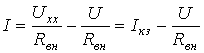
или

,

(2)

где ; - внутренняя проводимость источника.

Уравнению (2) соответствует схема замещения источника на рис. 6,а.

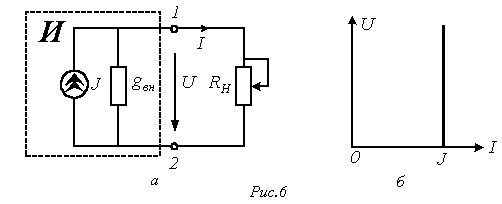
На этой схеме символом J обозначен элемент, называемый идеальным источником тока. Ток в ветви с этим элементом равен и не зависит от напряжения на зажимах источника, следовательно, ему соответствует ВАХ на рис. 6,б. На этом основании с учетом (2) у такого источника , т.е. его внутреннее сопротивление .

Отметим, что в расчетном плане при выполнении условия последовательная и параллельная схемы замещения источника являются эквивалентными. Однако в энергетическом отношении они различны, поскольку в режиме холостого хода для последовательной схемы замещения мощность равна нулю, а для параллельной – нет.

Кроме отмеченных режимов функционирования источника, на практике важное значение имеет согласованный режим работы, при котором нагрузкой RН от источника потребляется максимальная мощность

,

(3)

Условие такого режима

,

(4)

В заключение отметим, что в соответствии с ВАХ на рис. 5,б и 6,б идеальные источники ЭДС и тока являются источниками бесконечно большой мощности.

2. Влияние резистивного, индуктивного и емкостного элементов цепи на форму кривой тока. Резонансные явления.

При резистивной нагрузке токи всех гармоник совпадают по фазе с соответствующими гармониками напряжений и форма кривой несинусоидального тока аналогична форме кривой напряжения.

В цепи с индуктивным элементом амплитуда тока основной гармоники определяется как

Так как сопротивление индуктивного элемента увеличивается с переходом к высшим гармоникам, то амплитуда каждой гармоники тока будет уменьшаться обратно пропорционально порядку гармоники, и высшие гармоники тока будут проявляться в меньшей степени в общей кривой тока. Таким образом, кривая тока меньше отличается от синусоиды, чем кривая напряжения. Аналогично в цепи с емкостным элементом амплитуды токов основной и высших гармоник определяются как:

Так как сопротивление емкостного элемента уменьшается с переходом к высшим гармоникам, то амплитуды гармоник тока будут увеличиваться пропорционально порядку гармоники, форма кривой тока будет искажаться еще больше в сравнении с кривой напряжения.

Поскольку с ростом частоты сопротивление индуктивного элемента увеличивается, а емкостного уменьшается, в электрической цепи (см. рис. 4.5а) может возникнуть резонанс напряжений либо для первой, либо для одной из высших гармоник. Условие возникновения резонанса напряжений для некоторой k-гармоники:

При этом амплитуда тока резонансной гармоники может значительно превысить амплитуды тока всех остальных гармоник (см. пример 4.3), а на участках электрической цепи как с индуктивным, так и с емкостным элементом могут возникнуть перенапряжения.

В электрических цепях несинусоидального тока при параллельном соединении катушки и конденсатора возможно возникновение резонанса тока либо для первой, либо для одной из высших гармоник с присущими данному резонансу явлениями.

3. Задача.

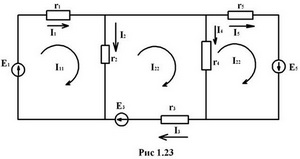
Найти токи в схеме (рис. 1.23) при помощи метода контурных токов.

r₁ = r₂ = r₃ = r₄ = r₅ = 10 Ом

E₁ = E₅ = 50 В; E₃ = 90 В

МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РФ ФГБОУ ВПО «БАШКИРСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ» ЗАУРАЛЬСКИЙ ФИЛИАЛ

Экзаменационный билет №3 Кафедра: ФИЗИКИ, МАТЕМАТИКИ И ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ Дисциплина: Теоретические основы электротехники Направления «Агроинженерия» II курс

УТВЕРЖДЕНО НА ЗАСЕДАНИИ КАФЕДРЫ « » 2012 г. Зав. кафедрой ____________Музафаров С. М.

Основные понятия об электрической цепи.

Возникновение переходных процессов. Законы коммутации.

Задача.

1. Основные понятия об электрической цепи.

Электрической цепью называют совокупность гальванически соединенных друг с другом источников электрической энергии и ее потребителей (нагрузок), в которых может возникать электрический ток. С помощью источников тот или иной вид энергии (энергия сжигаемого топлива, падающей воды, атомная и химическая энергия и т.д.) преобразуется в электрическую энергию.

Приемники, наоборот, преобразуют электрическую энергию в другие ее виды (механическую, тепловую, химическую, энергию светового излучения и т.д.).

Графическое изображение электрической цепи с помощью условных обозначений ее элементов называется электрической схемой цепи.

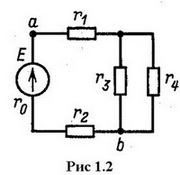
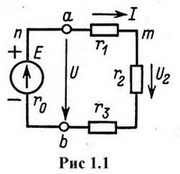
Электрические цепи подразделяются на разветвленные и неразветвленные. Простейшая неразветвленная цепь представлена на рис.1.1. Во всех элементах неразветвленной цепи действует один и тот же ток. Разветвленная цепь (рис.1.2) имеет в своем составе ветви, узлы, контуры. Ветвь - это участок цепи, состоящий из последовательно соединенных элементов и заключенный между двумя узлами. В каждой ветви существует свой ток.

Узел - это точка в электрической схеме цепи, где гальванически соединяются не менее трех ветвей. Любой замкнутый путь на схеме называется контуром. Независимым называется контур, содержащий хотя бы одну ветвь, не включенную в иной контур.

Пример разветвленной электрической цепи приведен на рис.1.2. В схеме два узла обозначенные буквами «а» и «b», три ветви, расположенные между узлами и два независимых контура.

2. Возникновение переходных процессов. Законы коммутации.

В электрических цепях могут происходить включения и отключения пассивных или активных цепей, короткие замыкания отдельных участков, различного рода переключения, внезапные изменения параметров и т.д.

В результате таких изменений, называемых коммутационными или просто коммутациями, которые будем считать происходящими мгновенно, в цепи возникают переходные процессы, заканчивающиеся спустя некоторое (теоретически бесконечно большое) время после коммутации.

Примем следующие обозначения:

t = 0 – начало отсчета времени переходного процесса;

0_– – момент времени непосредственно перед мгновенной коммутацией;

0₊ – момент времени непосредственно сразу после мгновенной коммутации.

В индуктивном элементе ток (и магнитный поток) непосредственно после коммутации в момент, который и назван моментом коммутации, сохраняет значение, которое он имел непосредственно перед коммутацией, т.е. при t = 0_– и дальше начинает изменяться именно с этого значения. Записанное в математической форме это явление называется первым законом коммутации:

.

Так, при включении ветви с катушкой, в которой не было тока, ток в этой ветви в момент коммутации равен нулю. Если для такой ветви допустить, что в момент коммутации ток изменяется скачком, то напряжение на индуктивном элементе будет бесконечно большим и не будет выполняться II закон Кирхгофа.

На емкостном элементе напряжение (и заряд) сохраняет в момент коммутации то значение, которое оно имело непосредственно перед коммутацией, и в дальнейшем изменяется, начиная именно с этого значения. Это явление называется вторым законом коммутации:

.

Так, при включении ветви с конденсатором, который не был заряжен, напряжение в момент коммутации равно нулю. Если допустить, что в момент коммутации напряжение на емкостном элементе изменится скачком, то ток будет бесконечно большим, и в цепи не будет выполняться II закон Кирхгофа.

С энергетической точки зрения невозможность мгновенного изменения тока i_L и напряжения u_C объясняется невозможностью скачкообразного изменения запасенной в индуктивном и емкостном элементах энергии, так как такое изменение энергии требует бесконечно большой мощности.

3. Задача.

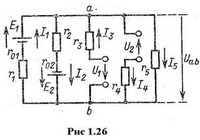
В электрической цепи рис.1.26

Пользуясь методом узлового напряжения, определить токи в ветвях.

МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РФ ФГБОУ ВПО «БАШКИРСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ» ЗАУРАЛЬСКИЙ ФИЛИАЛ

Экзаменационный билет №4 Кафедра: ФИЗИКИ, МАТЕМАТИКИ И ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ Дисциплина: Теоретические основы электротехники Направления «Агроинженерия» II курс

УТВЕРЖДЕНО НА ЗАСЕДАНИИ КАФЕДРЫ « » 2012 г. Зав. кафедрой ____________Музафаров С. М.

Ток, напряжение и мощность в электрической цепи.

Уравнения линии с распределенными параметрами.

Задача.

1. Ток, напряжение и мощность в электрической цепи.

Электрический ток и напряжение являются основными величинами, характеризующими состояние электрических цепей. Электрический ток в проводниках представляет явление упорядоченного движения электрических зарядов под действием электрического поля. Под словами ток понимают также интенсивность или силу тока, измеряемую количеством электрического заряда q, прошедшего через поперечное сечение проводника в единицу времени:

где Δq - электрический заряд, прошедший за время Δt через поперечное сечение проводника.

Следовательно, ток характеризует скорость изменения заряда во времени.

В системе СИ заряд измеряется в кулонах (Кл), время - в секундах, а ток - в амперах (А).

Ток является скалярной алгебраической величиной, знак которой зависит от направления движения одноименных зарядов, а именно условно принятого положительного заряда. Для однозначного определения знака тока достаточно произвольно выбрать одно из двух возможных направлений за положительное, которое отмечается стрелкой (см. рис.1.2). Перед началом анализа электрической цепи необходимо отметить во всех ветвях положительные направления токов, выбор которых может быть произвольным. Закон изменения тока во времени может быть выражен функцией времени произвольной формы.

Постоянным называется ток, значение которого неизменно во времени при неизменных параметрах электрической цепи. Постоянный ток принято обозначать буквой I.

Прохождение электрического тока в цепи связано с преобразованием или потреблением энергии. Для определения энергии, затрачиваемой при перемещении заряда между двумя рассматриваемыми точками проводника, вводят новую величину - напряжение.

Электрическим напряжением между двумя точками называют количество энергии, затрачиваемой на перемещение заряда из одной точки в другую.

где W – энергия электрического поля. При измерении энергии в джоулях (Дж) и заряда в кулонах (Кл) напряжение измеряется в вольтах (В).

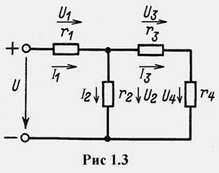
Для однозначного определения знака напряжения между двумя выводами рассматриваемого участка цепи одному из выводов условно приписывают положительную полярность, которую отмечают либо знаком "+", либо стрелкой, направленной от вывода (рис.1.3). Напряжение положительно, если его полярность совпадает с выбранной.

Обычно условно положительную полярность напряжения выбирают согласованной с выбранным положительным напряжением тока, когда стрелки для тока и напряжения совпадают. В цепях постоянного тока напряжение принято обозначать буквой U.

Из определения напряжения (1.2) получается выражение энергии W, затраченной на перемещение заряда q на участке цепи с напряжением U к моменту времени t :

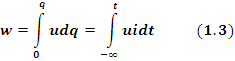
Дифференцирование этого равенства во времени дает выражение мгновенной мощности p - скорости изменения энергии во времени :

Мощность измеряется в Ваттах (Вт). Мощность в электрической цепи постоянного тока обозначается буквой P и равна P=UI. Она является алгебраической величиной, знак которой определяется знаком напряжения и тока: при совпадении этих знаков мощность положительна (Р > 0), что соответствует потреблению энергии в рассматриваемом участке цепи; при несовпадении знаков тока и напряжения мощность отрицательна (P < 0), что означает выделение ее из участка цепи (такой участок является источником энергии).

2. Уравнения линии с распределенными параметрами.

Напряжения и ток в линии являются функциями двух независимых переменных – пространственной координаты x, определяющей место наблюдения, и времени t, определяющей момент наблюдения. Считается, что направление координаты x совпадает с осью линии.

Необходимо найти пространственно-временное распределение величины тока в линии i(x, t) и напряжения между проводами u(x, t). В этом случае также можно определить процесс передачи энергии по линии, когда приемники и источники находятся на обоих концах линии.

Приняв положительное направление тока в линии слева направо, условимся называть "началом" левый конец линии. Расстояние от начальной точки до произвольной обозначим через x, а от конца – через x'. Вся длина линии l = x + x'.

Выделим элементарный участок Δx на расстоянии x от начала. Пользуясь первичными параметрами R₀,L₀, C₀, G₀, отнесенными к единице длины линии, представим приближенно участок Δx в виде схемы замещения (рис. 13.1).

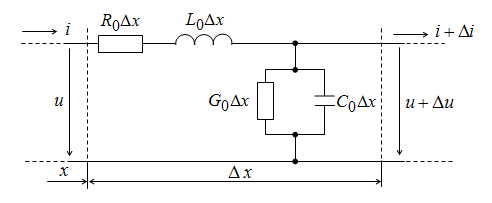
Рис. 13.1. Схема замещения участка линии

Обозначим:

u – напряжение между верхним и нижним проводом в точке x;

Δu – приращение напряжения на участке Δx;

i – ток в точке x;

Δi – приращение тока на участке Δx.

Уравнения для приращений напряжения и тока на элементе Δx линии запишутся:

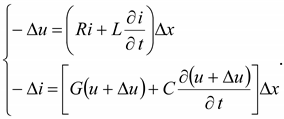(13.1)

Это уравнение в частных производных. По мере стремления Δx к нулю степень точности этих уравнений повышается, причем величина второго порядка малости 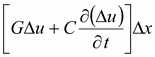  в правой части второго уравнения может быть опущена.

В этом случае длинная линия рассматривается как цепная схема с бесконечно большим количеством звеньев, электрические параметры которых бесконечно малы.

Разделив обе части уравнений на Δx и перейдя к пределу Δx  0, получим дифференциальные уравнения линии

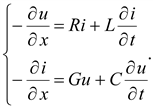 (13.2)

Эти уравнения носят название телеграфных.

Если за начало отсчета принять конец линии, т.е. ввести координату x', уравнения примут вид:

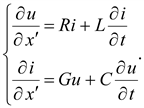 (13.3)

Уравнения (13.2) и (13.3) решаются однозначно при использовании начальных и граничных условий. Начальными условиями будут служить значения напряжения и тока в начале и конце линии в момент времени, принятый за нуль. Граничные условия определяются связями между напряжением и током в начале или в конце линии и зависят от заданного режима работы линии.

3. Задача.

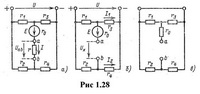
В электрической цепи (рис.1.28 а).

Пользуясь методом эквивалентного генератора определить ток I и напряжение U_ab.

МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РФ ФГБОУ ВПО «БАШКИРСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ» ЗАУРАЛЬСКИЙ ФИЛИАЛ

Экзаменационный билет №5 Кафедра: ФИЗИКИ, МАТЕМАТИКИ И ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ Дисциплина: Теоретические основы электротехники Направления «Агроинженерия» II курс

УТВЕРЖДЕНО НА ЗАСЕДАНИИ КАФЕДРЫ « » 2012 г. Зав. кафедрой ____________Музафаров С. М.

Источники в электрических цепях.

Основные характеристики электромагнитного поля.

Задача.

1. Источники в электрических цепях.

Под источником в электротехнике понимают электротехническое устройство, производящее электрическую энергию и питающее электрическую цепь. Источники являются причиной появления токов и напряжений в цепи. Электрическая энергия постоянного тока может быть получена путем преобразования различных видов энергии: химической (гальванические элементы и аккумуляторы), механической (генераторы постоянного тока), тепловой (термоэлектрогенераторы), лучистой, например, световой (солнечные батареи). Все источники электрической энергии характеризуются определенным значением либо электродвижущей силы Е (э.д.с.)-источники напряжения, либо тока I-источники тока. В источниках (активных элементах цепи) за счет энергии сторонних сил совершается перенос положительных зарядов от меньшего потенциала к большему. Работа сторонних сил, затрачиваемая на перенос единичного заряда от зажима с меньшим потенциалом к зажиму с большим потенциалом, называется электродвижущей силой - Э.Д.С. источника и обозначается, в цепях постоянного тока, буквой Е. Э.Д.С. источника численно равна напряжению между зажимами источника при отсутствии в нем тока.
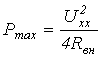