Порядок виконання лабораторної роботи
Відкрити програму Inkscape. Створіть новий малюнок.
Зробіть по 1 екземпляру кожної фігури.
Зробіть 2 фігури з обводкою пунктирними лініями.
Зафарбуйте всі крім 1 фігури різними кольорами і градієнтами (не менше 2-х різних градієнтів).
Згрупуйте об’єкти. Зробіть 5 копій групи, кожну наступну на 10% зменшіть і поверніть на 30 градусів.
Отримані групи розташуйте в композицію за власним смаком.
Оформіть звіт з 5 скріншотами, які відображують виконані дій в пунктах 2-6.
Подати звіт до захисту та підготуватись до контрольних питань.
Контрольні питання
Які основні фігури доступні для малювання в Inkscape?
Яким чином можна зафарбувати фігуру?
Які перетворення можна виконати з фігурою?
Як вибрати об’єкт, який знаходиться поза іншим об’єктом і його не видно?
Яким чином можна дублювати об’єкти?
Чи можна використовувати клавіатуру для створення зображення?
Література
сайт о бесплатном графическом редакторе http://inkscape.paint-net.ru/?id=21
http://inkscape.paint-net.ru/?id=22
Лабораторна робота № 10
Тема роботи: Робота з кривими Без’є в графічному редакторі Inscape
Мета: ознайомитися в з принципом побудови кривих ліній Без’є та навчитись будувати їх в графічному редакторі Inscape
Теоретичні відомості
Криві Без'є́ були запроваджені в 1962 році П'єром Без'є з автомобілебудівної компанії «Рено». Криві Без'є - один з найголовніших інструментів систем автоматизованого проектування і програм комп'ютерної графіки. Відрізки кривих Безьє – це окремий випадок відрізків кривих третього порядку. Вони описуються не одинадцятьма параметрами, як довільні відрізки кривих третього порядку, а лише вісьмома, і тому працювати з ними зручніше.
Метод побудови кривих Безьє базується на застосуванні пари дотичних проведених до лінії в точках її закінчення (рис. 1.1).
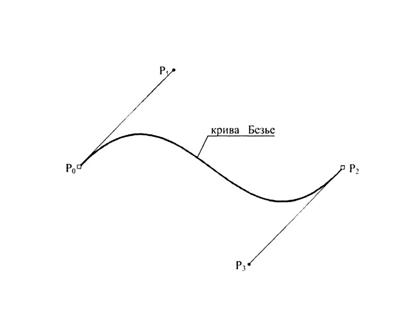
Рис. 10.1. Канонічний вид кривої Безьє
Для побудови кривої потрібно чотири контрольні точки. Проте крива фізично проходить тільки через дві з них, вони отримали назву опорних. Одна з цих точок називається початковою (start point), а інша – кінцевою (end point). Дві точки залишаються в стороні, вони отримали назву керуючих (control point). Для того, щоб їх не «втратити», в програмах векторної графіки керуючі точки з’єднуються з опорними точками лінією.
Для того щоб отримати величезну різноманітність форм, із яких можна скласти об’єкт будь-якої складності потрібно змінити форму канонічної кривої Безьє.
У програмах векторної графіки існує єдиний спосіб – це інтерактивне переміщення опорних і керуючих точок (рис. 10.2). Якщо переміщуються початкова чи кінцева точки, то крива стане відповідним чином змінюватися (витягуватися чи стискуватися як пружна резинка). Переміщення керуючих точок змінює кривизну відповідної частини кривої Безьє.
а) б) в)
Рис.10.1. Способи зміни форми сегмента: а) переміщення сегмента,
б) переміщення опорної точки, в) переміщення керуючої точки
Таким чином, за допомогою переміщення цих чотирьох точок отримують необмежену кількість форм кривих Безьє, яка може бути всього-навсього одним окремим сегментом складного векторного контуру.
У кожному сегменті можна добавляти опорні точки, які теж дозволяють змінювати форму кривої. Добавляння нових опорних точок у межах одного сегмента кривої не протирічить тій умові, що окремі криві з’єднуються в ланцюг. Просто крива Безьє добавляється не до кінця контуру, а розміщується всередині вже існуючого контуру.
Взагалі будь-яка конструкція (векторний контур або векторна форма) створюється з векторних сегментів, кожен із яких ідентичний окремій елементарній кривій Безьє.
Звідси слідує, що між ними утворюються з’єднувальні точки, які деколи називаються вузлами (наприклад, nodes – у графічному редакторі CorelDraw).
Для підтримання співвідношення між елементарними сегментами існують різні типи опорних точок.
Типи опорних точок
Існують такі типи опорних точок:
1) точки перегину,
2) гладка опорна точка,
3) симетрична опорна точка,
4) тангенціальна опорна точка.
Точки перегину Цей тип опорної точки, який з’єднує два сегменти, забезпечує незалежність керуючих точок у напрямку і довжині один від одного. Такий стан сегментів називається вигин (рис. 3.3).
Гладка опорна точка Кутове зчленування сегментів (вигин) далеко не завжди вигідне. Наприклад, для створення кола необхідно забезпечити з’єднання яке в кресленні і в геометрії називають гладким спряженням, коли одна крива плавно переходить у іншу. Таке зчленування забезпечує гладка опорна точка (smooth)(рис. 10.2).
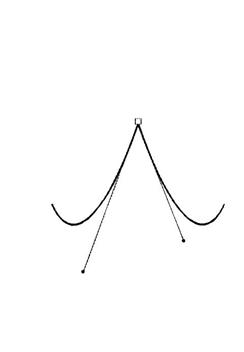
Рис. 10.2. Приклад точки перегину Рис. 3.4. Приклад гладкої точки
Симетрична опорна точка У програмах CorelDRAW передбачений підвид гладкого спряження, який називається симетричний вузол (symm від слова «symmetcal») (рис. 10.3). Сутність його в тому, що керуючі лінії фіксують не тільки по напрямку, але й по величині (довжина направляючих завжди однакова). Якщо одну з них збільшувати чи зменшувати, друга буде синхронно повторювати цю дію.
Тангенціальна опорна точка У свою чергу, в програмі FreeHand у окремий вид опорних точок виділений випадок гладкого спряженням, прямолінійного і криволінійного сегментів (рис. 10.4). Така точка отримала назву тангенціальної (connecter point). Під час виділення така точка позначається трикутником.
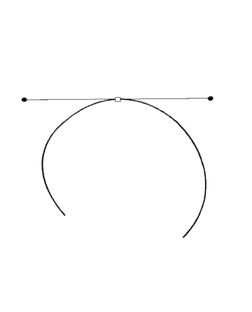
Рис.10.3 Симетрична опорна точка Рис. 10.4 Тангенціальна опорна точка
Зміст цієї точки в тому, що для того, щоб криволінійний сегмент гладко з’єднувався з прямою лінією, дотична криволінійного сегмента повинна співпадати з продовженням прямого сегмента. Тому керуюча точка криволінійного сегмента спроможна рухатися тільки вздовж цієї дотичної.