НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ
Московский институт стали и сплавов
ВЫКСУНСКИЙ ФИЛИАЛ
Кафедра Технологии и оборудования обработки металлов давлением
Е.А. Харитонов
Лабораторная (практическая) работа № 3
УПРУГИЕ ДЕФОРМАЦИИ РАБОЧЕЙ КЛЕТИ
(Уточнённая и дополненная)
Зав. кафедрой ТиООМД С.В. Самусев
Автор Е.А. Харитонов
2013
3.1 Цель работы
Определение усилий прокатки различных металлов, определение упругой деформации клети в зависимости от усилия прокатки.
3.2 Теоретическое введение
Рабочая клеть прокатного стана, как и всякая другая конструкция, представляет собой упругую систему. Под действием силы прокатки ее детали упруго деформируются: стойки станин растягиваются, поперечины станин прогибаются, валки прогибаются и сплющиваются, многие детали (подшипники, подушки, нажимные винты, гайки, подпятники и др.) сжимаются. В результате всех этих деформаций зазор между валками увеличивается. Разность между зазором во время прокатки и начальным зазором между ненагруженными валками называется пружиной рабочей клети. Зазор между валками в момент прокатки равен толщине выходящей полосы (если пренебречь очень малым упругим восстановлением толщины полосы после прокатки); поэтому пружину можно представить в виде:
δ = h1 – s0,
где h1 — толщина полосы на выходе из валков; s0 — зазор между ненагруженными валками.
Пружина рабочей клети δ зависит в основном от усилия прокатки и может быть представлена в виде графика (рисунок 3.1).
Р, Мн
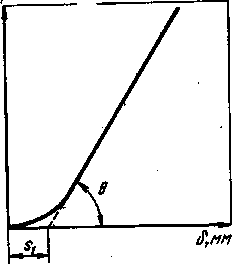
Рисунок 3.1 – Типичный вид зависимости пружины рабочей клети от силы прокатки
Линия, представленная на графике, называется упругой линией клети. Она состоит из двух участков — криволинейного и прямолинейного. Криволинейный участок показывает, что на начальной стадии нагружения пружина резко увеличивается даже при небольшом росте силы Р. Это, объясняется выборкой зазоров и неплотностей (люфтов) в сочленениях деталей и местной повышенной деформацией в точках локального контакта. Основная часть упругой линии клети прямолинейна. Ее наклон характеризуется углом θ. Очевидно, чем больше угол θ, тем выше жесткость рабочей клети. Тангенс угла θ называют модулем жесткости клети Мк. Нетрудно видеть, что:
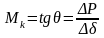
В качестве базы можно принять Δδ = 1мм. Тогда становится понятной физическая сущность модуля жесткости клети: это есть усилие, вызывающее увеличение пружины на 1мм. В зависимости от конструкции клети и величины приложенных сил упругая деформация может колебаться в весьма широких пределах: от 0,1–0,5 миллиметра в листовых, чистовых клетях проволочных станов до 5-10 мм на блюмингах, черновых клетях обжимных станов.
В расчетах часто используется величина, обратная модулю жесткости: 1/Мк. Ее называют податливостью клети. По своему смыслу податливость клети показывает, насколько изменяется пружина при увеличении или уменьшении усилия Р на 1МН (или 1т).
Многочисленные исследования упругих деформаций клетей приводят к выводу, что основную долю пружины, до 50—70%, составляет деформация валковой системы: прогиб и проседание опорных валков, сжатие в контакте рабочих и опорных валков, прогиб рабочих валков. Доля деформации других деталей и узлов меньше: станин – до 15 – 18%; подшипников – до 15%; нажимного узла – до 15%; остальных деталей – до 10 – 15%.
Определение пружины клети δ при заданных условиях прокатки необходимо для правильной установки валков, выбора величины начального зазора s0. С другой стороны, если известна пружина, то можно предсказать толщину полосы после прокатки h1 при заданном валковом зазоре.
h1 = s0 + δ
Из построения на рисунке 3.1 находим:
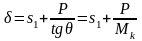
где s1 – приращение валкового зазора при очень малом усилии (сумма зазоров в контактах нагружаемых деталей).
Подставив выражение в приведенные выше формулы, получим:
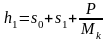
Если пренебречь величиной s1 или включить ее в s0, то получим:
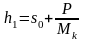
В литературе эта формула именуется уравнением Головина-Симса.