4. Решение уравнения теплопроводности методом конечных разностей
Рассмотрим решение уравнения теплопроводности
удовлетворяющее
начальному условию
и граничным условиям
.
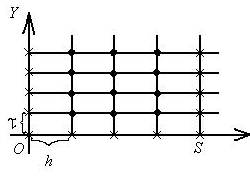
Рис. 5
Построим в полуполосе
два семейства параллельных прямых
обозначим
Обозначим
.
В каждом узле
заменим
.
Подставим в
уравнение
.
Обозначим
получим
.
Решим уравнение
относительно
.
Полученное сеточное уравнение дополним уравнениями, аппроксимирующими граничные и начальные условия на той же сетке узлов:
Получим систему разностных уравнений, называемую разностной схемой для уравнения теплопроводности при заданных начальном и граничных условиях:
(4)
Использованный в схеме шаблон узлов называется явным двухслойным шаблоном, он имеет вид
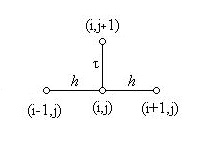
Рис. 6
Доказано, что
полученная сеточная схема сходится к
решению исходной задачи с погрешностью
и устойчива при
.
Наиболее удобный вид сеточное уравнение
имеет при
и при
Уравнение теплопроводности можно аппроксимировать, безусловно, устойчивой двухслойной неявной разностной схемой, если заменить в нем
Обозначим
и получим неявную сеточную схему
с шаблоном узлов
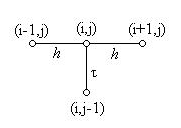
Рис. 7
Сеточное решение
сходится к точному с порядком погрешности
но нужно помнить, что погрешность
приближенного решения, полученного
методом конечных разностей, складывается
из трех погрешностей:
1) погрешности замены дифференциального уравнения разностным;
2) погрешности аппроксимации краевых и начальных условий;
3) погрешности решения системы уравнений.
Пример 2
Найти решение
уравнения теплопроводности
удовлетворяющее
начальному условию
и граничным
условиям
.
Взять
Решение
Составим явную
разностную схему задачи. Так как
то
Составим схему
Решение запишем в таблице
-
j
i
0
1
2
3
4
5
0
0,2
0,4
0,6
0,8
1,0
0
0,00
1
0,02
0,80
0,80
0,48
2
0,04
0
0,40
0,64
0,64
0,40
0
3
0,06
0
0,32
0,52
0,52
0,32
0
4
0,08
0
0,26
0,42
0,42
0,26
0
5
0,10
0
0,21
0,34
0,34
0,21
0
Первую строку
таблицы заполним, используя начальное
условие
.
Первый и последний столбцы заполним,
используя краевые условия:
остальные
строки и столбцы заполним, используя
сеточное уравнение
.