2. Метод конечных разностей приближенного решения дифференциального уравнения с частными производными

Суть метода конечных разностей такова: задачу решения дифференциального уравнения с непрерывной областью изменения аргументов и непрерывными краевыми и начальными условиями подменяют другой задачей. Вместо непрерывной области изменения аргументов рассматривают соответствующую дискретную область (сетку). Производные заменяют конечно-разностными соотношениями в выбранных точках (узлах сетки). Дифференциальное уравнение заменяют уравнением в конечных разностях. Граничные и начальные условия формулируют для новой задачи в соответствующих узлах сетки. Решение этой новой задачи сводится к решению системы алгебраических уравнений с большим числом уравнений и неизвестных. Нужно понимать, что сразу же возникают следующие вопросы:

- как выбрать точки дискретного изменения аргумента, как выбор этих точек сказывается на точности решения ;

- какой должна быть точность аппроксимации производных разностными отношениями, чтобы решение разностной задачи было достаточно близким к решению основной задачи;

- как влияют погрешности, внесенные в начале вычислений на точность результата. Если малые погрешности в начале расчета не сказываются заметно на результате, то говорят, что вычислительная разностная схема устойчива. В противном случае схема неустойчива. Можно пользоваться только устойчивыми схемами.

Проблемы аппроксимации и устойчивости вычислительных схем метода сеток решаются по-разному для различных типов дифференциальных уравнений. Заниматься этими вопросами не будем.

Рассмотрим построение простейшей разностной схемы.

Пусть на плоскости xoy задана область с границей .

Построим на плоскости два семейства параллельных прямых: ,

с шагом и с шагом . Точки пересечения прямых назовем узлами. Два узла назовем соседними, если они удалены друг от друга в направлении оси Ox или Oy на или соответственно. Выделим узлы, принадлежащие области и некоторые узлы, не принадлежащие этой области, но расположенные от границы в направлении Ox или Oy на расстоянии меньшем, чем или . Те узлы, у которых все четыре соседних узла принадлежат выделенному множеству узлов, называются внутренними. Оставшиеся узлы выделенного множества называются граничными.

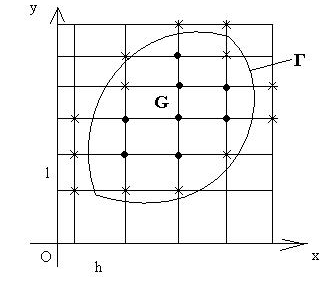
Рис. 1

Граничные узлы на рис. 1 обозначены крестом, внутренние узлы точкой. Значения искомой функции в узлах сетки обозначим . В каждом внутреннем узле заменим частные производные разностными отношениями

(1)

В граничных узлах используем формулы

. (2)

3. Уравнение Лапласа в конечных разностях

Составим разностную схему задачи Дирихле для уравнения Лапласа

.

В области , ограниченной кривой введем квадратную сетку с шагом . Во внутренних узлах сетки заменим частные производные конечными разностями

.

Подставим в уравнение

и найдем

. (3)

К полученной системе разностных уравнений (3) добавим систему значений функции в граничных узлах сетки и получим разностную схему уравнения.

Конфигурации внутренних узлов, связанных одним уравнением, называют шаблоном разностной схемы и для удобства построения схемы изображают на чертеже. Для схемы (3) шаблон изображен на рис. 2.

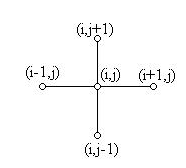
Рис. 2

В граничных узлах значение функции считают равным значению функции в ближайшей к этому узлу точке границы , т. е. (рис. 3) – это простой снос граничных условий или применяют линейную интерполяцию

(рис. 3),

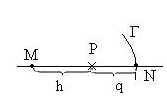
Рис. 3

или (рис. 4).

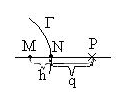
Рис. 4

-внутренний узел, -граничный узел, - ближайшая к точка границы Г.

Пример 1

Найти решение уравнения Лапласа в области, ограниченной эллипсом (Г), если на границе Г области функция удовлетворяет условию .

Решение

Так как граница область, ограниченная , и граничные условия симметричны относительно обеих осей координат, достаточно найти решение задачи только в первой четверти координатной плоскости.

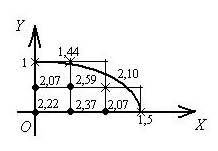
Составим таблицу точек границы

	0	1	2	3
	2	1,89	1,49	0

Сделаем чертеж, построив и квадратную сеть с шагом

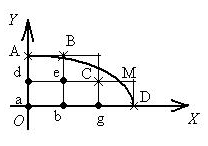
Граничные узлы A; B; C; D.

Внутренние узлы .

Вычислим значения функции в граничных узлах

(простой снос граничного условия из точки

(1; 1,89) границы ).

. Найдем координаты точки границы: ,

.

Для вычисления в точке применим линейную интерполяцию

.

, обозначим ,

, где

Обозначим значения решения во внутренних узлах сетки

(узлов мало, обозначения можно не использовать).

Выберем шаблон

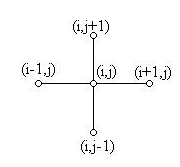
Составим разностную схему .

Получим систему уравнений

Решив систему, получим

Получили значения в узлах сетки