3. Квадратурный метод решения уравнений Вольтерра второго рода
Уравнение Вольтерра второго рода
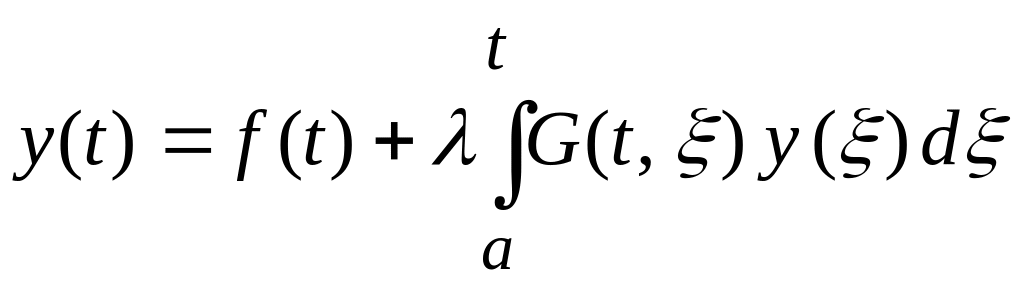
имеет единственное
решение при любом
,
если ядро
- непрерывная функция в области
,
и функция
непрерывна на отрезке
.
Для вычисления
интеграла выберем формулу серединных
прямоугольников. Разобьем отрезок
точками
.
В каждом частичном промежутке разбиения
выберем среднюю точку
.
Искомую функцию
заменим ступенчатой функцией, принимающей
постоянное значение
на каждом частичном промежутке
.
Считаем, что верхняя граница интеграла
изменяется дискретно, принимая значения
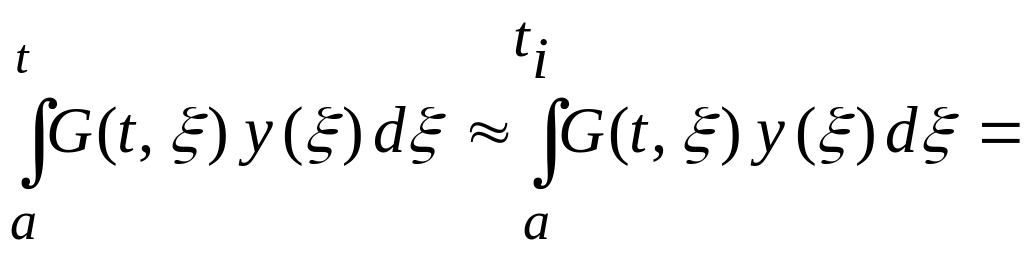
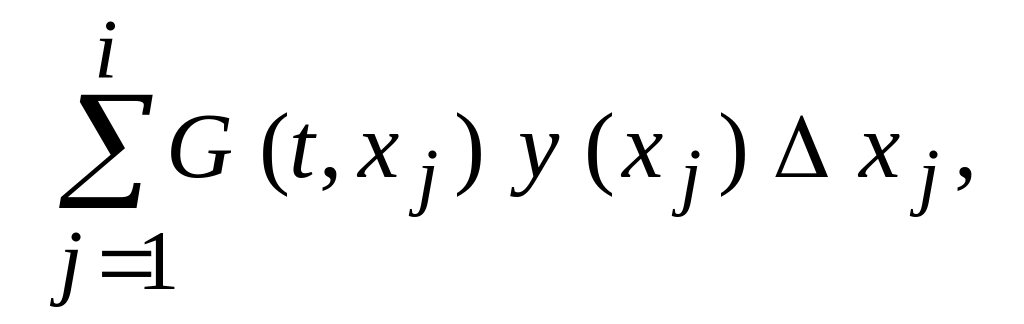
где
.
Заменим в уравнении интеграл полученной суммой
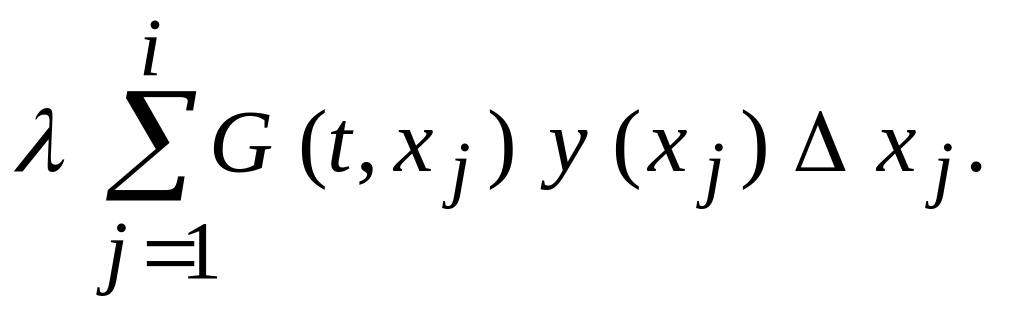
Найдем значения
искомой функции
в точках
,
получим систему
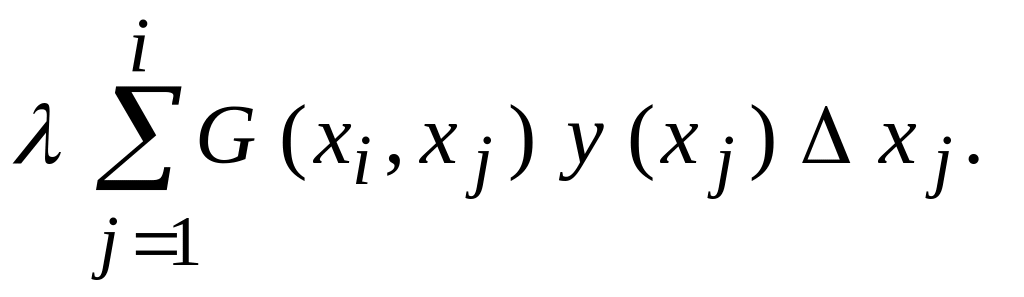(7)
Обозначим
Запишем систему (7) в развернутом виде
(8)
Получим систему с треугольной матрицей.
Решив систему,
получим таблицу значений искомой функции
в точках
Если отрезок
разбит на равные части, то
Пример 1
Дано уравнение
Фредгольма
Найти значение
искомой функции
на отрезке
.
1. Методом итераций.
2. Применив
квадратурную формулу Симпсона. Отрезок
разбить на две части.
3. Сравнить полученные
результаты в узлах
Решение
1. Метод итераций.
Рассмотрим условие сходимости итерационного процесса
Дано:
при
т.е.
.
Получим
следовательно итерационный процесс
сходится к решению.
Запишем уравнение в виде
Возьмем
тогда
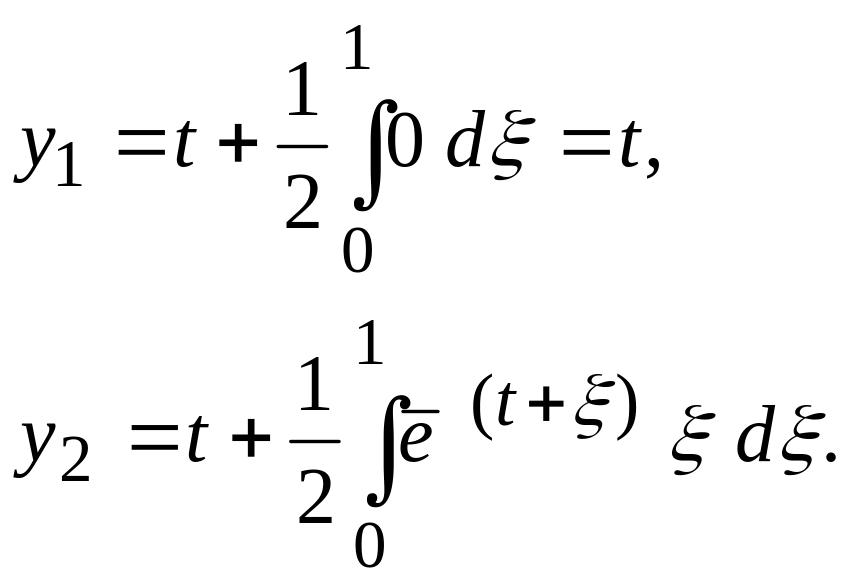
Вычислим интеграл по частям
Взяв
получим
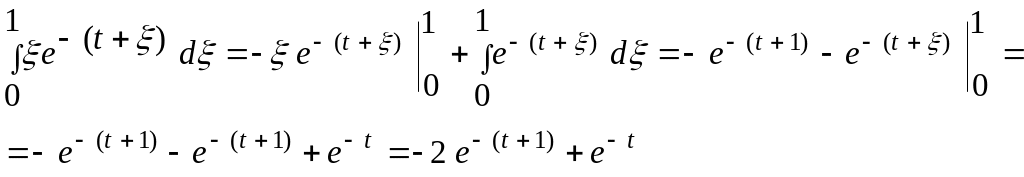
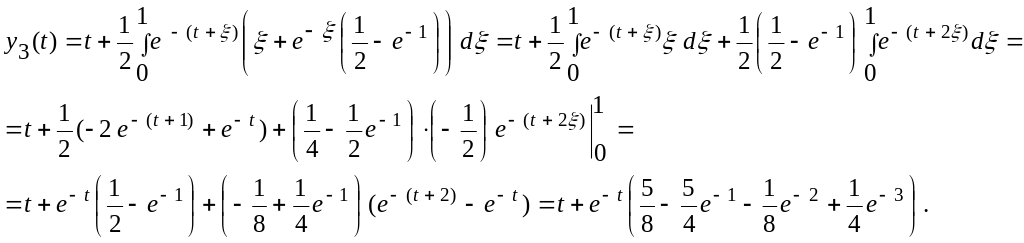
Возьмем
В узлах
получим таблицу приближенных значений
|
0 |
0,5 |
1 |
|
0,1606 |
0,5974 |
1,0591 |
2. Квадратурный
метод решения. Возьмем
Узлы
формулы
Формула Симпсона
для
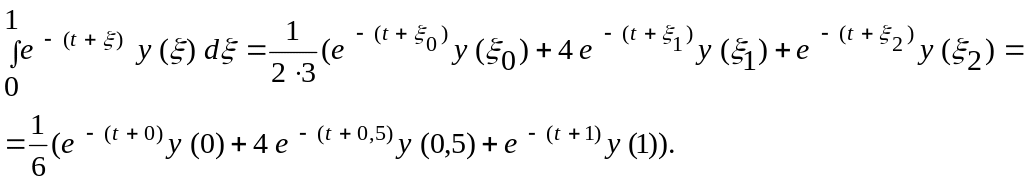
Обозначим
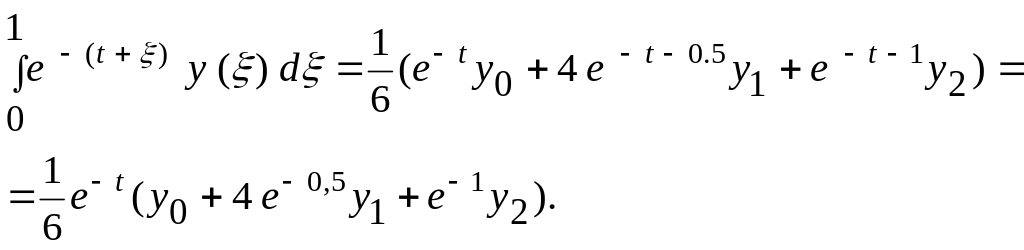
Подставим в заданное интегральное уравнение и получим уравнение
(*)
Возьмем
Подставим эти значения в полученное уравнение
Вычислим коэффициенты. Запишем систему в стандартной форме и решим методом Гаусса
Составим таблицу значений приближенного решения интегрального уравнения
T |
0 |
0,5 |
1 |
|
0,1646 |
0,5867 |
1,0546 |
Шаг интегрирования
был достаточно большим, значения
приближенного решения полученного
методом итераций и квадратурным методом
различаются на 0,5 % в точке
на 1,8 % в точке
и на 2,5 % в точке
Если найденные значения
подставим в формулу (*), получим формулу
приближенного решения уравнения
.
Лекция № 2 численное решение уравнений с частными производными
1. Примеры уравнений математической физики
1. Уравнение Лапласа (в прямоугольных координатах)
.
Уравнение используют
для математического описания плоских
электростатических и магнитных полей,
стандартных тепловых полей и др., называют
уравнением потенциала. Выражение,
стоящее в левой части уравнения,
обозначают
и уравнение записывают в виде
- оператор Лапласа).
2. Уравнение
Пуассона:
т. е.
используют в задачах электростатики,
электронной оптики, теории упругости
и др.
3. Уравнение теплопроводности (диффузии)
.
Это однородное
уравнение теплопроводности.
-
постоянная, иногда называется коэффициентом
температуропроводности. Уравнение
описывает линейные диффузионные
процессы, в частности, распространение
тепла в тонком стержне
-
неоднородное уравнение теплопроводности.
Функция
характеризует присутствие внутри
стержня тепловых источников или
поглотителей тепла.
4. Волновое уравнение
описывает свободные колебания тонкой струны. Если колебания совершаются под действием внешней силы, характеризуемой функцией , уравнение имеет вид
.
Все перечисленные уравнения являются частными случаями уравнения
,
линейного
дифференциального уравнения с частными
производными второго порядка относительно
искомой функции
двух переменных.