Лекция № 1 интегральные уравнения

Интегральным уравнением называют уравнение, содержащее искомую функцию под знаком интеграла . Интегральными уравнениями описываются законы сохранения массы, энергии, импульса. К интегральным уравнениям приводят инженерные задачи в радиотехнике, газовой динамике, электродинамике, экологии, экономике и др. Например, задачу Коши можно представить в интегральной форме , задавать начальное условие в этом случае не нужно, оно уже включено в уравнение.

Мы рассмотрим только линейные интегральные уравнения относительно скалярной функции одной действительной переменной .

Интегральное уравнение называется линейным, если искомая функция входит в уравнение линейно. Из линейных уравнений запишем только уравнение Фредгольма первого и второго рода и уравнения Вольтерра первого и второго рода, а рассмотрим решение уравнений Фредгольма и Вольтерра второго рода (численные методы, которые мы рассмотрим, применимы также для решения нелинейных интегральных уравнений).

1. Уравнение Фредгольма второго рода

2. Уравнение Вольтерра второго рода

3. Уравнение Фредгольма первого рода

4. Уравнение Вольтерра первого рода

Функция в этих уравнениях называется ядром уравнения. В уравнениях Фредгольма ядро определено и ограничено в квадрате , В уравнениях Вольтерра ядро определено и ограничено в треугольнике

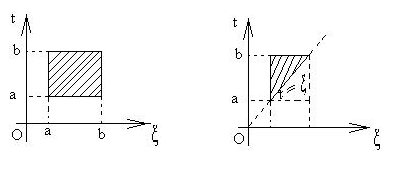
Рис. 1

Уравнение, полученное при интегральной записи задачи Коши, является уравнением Вольтерра второго рода.

В редких случаях удается получить точное аналитическое решение интегрального уравнения. Рассмотрим простейшие способы получения приближенного решения.

1. Метод последовательных приближений

Рассмотрим уравнение Фредгольма второго рода

(1)

Построим итерационный процесс, аналогичный методу простых итераций для алгебраического уравнения.

Пусть - начальное приближение искомой функции На практике часто берут Подставив в правую часть уравнения, получим первое приближение искомого решения

подставляя в правую часть уравнения, получим второе приближение

и так далее,

(2)

При достаточно малом и ограниченном ядре , итерационный процесс сходится к искомому решению . Достаточное условие сходимости имеет вид

где (3)

2. Квадратурный метод решения интегральных уравнений Фредгольма

Выберем квадратурную формулу

с узлами

Считая, что получим

, подставим в правую часть интегрального уравнения и получим

(4)

алгебраическое уравнение для поиска приближенных значений решения Решение найдем лишь в точках совпадающих с узлами примененной квадратурной формулы Подставив в уравнение (4), получим систему линейных уравнений

, . (5)

Обозначим , и запишем систему (5) уравнений с неизвестными в виде

. (6)

Решим систему и найдем значения . Получим таблицу значений приближенного решения интегрального уравнения

			…
			…