Листинг_№9

%На примере решения некорректного уравнения Фредгольма

%первого рода (54) с помощью метода регуляризации,

%т.е. путем сведения исходной задачи (54), (57) к

%решению корректного интегро-дифференциального уравнения

%(58), (58') исследуется зависимость оптимального

%значения параметра alpha_opt от шага сетки h

function noncor3

global N h

%Вводим начальное число узлов сетки по

%переменным xi и eta

N=21;

%Организуем цикл расчетов с разным сетками

for t=1:5

%Число узлов сетки по переменным xi и eta

%увеличиваем в арифметической прогрессии

N=N+30; h=1.0/(N-1); h2=h^2; h3=h^3;

xi=0:h:1; eta=0:h:1;

%Определяем значения аналитического решения cos(pi*xi)

%в узлах сетки xi

ya=cos(pi*xi);

%Определяем набор параметров регуляризации alpha

alph_l=7e-6; alph_r=2e-5; alph_h=(alph_r-alph_l)/20;

alpha=alph_l:alph_h:alph_r;

%Организуем цикл расчетов с различными значениями

%параметра регуляризации

for s=1:length(alpha)

%Согласно разностной схеме (59), (61), (61')

%определяем линейную систему уравнений Ay = b

%относительно неизвестного вектора y

%Определяем левое граничное условие согласно (61)

A(1,1)=0.25*h3*Q(xi(1),eta(1));

A(1,N)=0.25*h3*Q(xi(1),eta(N));

for j=2:(N-1)

A(1,j)=0.5*h3*Q(xi(1),eta(j));

end

A(1,1)=A(1,1)+alpha(s)*(1+0.5*h2);

A(1,2)=A(1,2)-alpha(s);

b(1)=0.5*h2*f(xi(1));

%Определяем элементы матрицы A согласно (59)

for i=2:(N-1)

A(i,1)=0.5*h3*Q(xi(i),eta(1));

A(i,N)=0.5*h3*Q(xi(i),eta(N));

for j=2:(N-1)

A(i,j)=h3*Q(xi(i),eta(j));

end

A(i,i)=A(i,i)+alpha(s)*(2+h2);

A(i,i-1)=A(i,i-1)-alpha(s);

A(i,i+1)=A(i,i+1)-alpha(s);

b(i)=h2*f(xi(i));

end

%Определяем правое граничное условие (61')

A(N,1)=0.25*h3*Q(xi(N),eta(1));

A(N,N)=0.25*h3*Q(xi(N),eta(N));

for j=2:(N-1)

A(N,j)=0.5*h3*Q(xi(N),eta(j));

end

A(N,N)=A(N,N)+alpha(s)*(1+0.5*h2);

A(N,N-1)=A(N,N-1)-alpha(s);

b(N)=0.5*h2*f(xi(N));

%Решаем линейную систему уравнений Ay = b

y=A\b';

%Оцениваем ошибку численного решения y путем

%оценки разности error=||y-ya|| в норме C, где

%ya - аналитическое решение задачи (54), (57)

for i=1:N

z(i)=abs(y(i)-ya(i));

end

error(s)=max(z);

end

%Определяем значение alph_opt, при котором ошибка

%численного решения минимальна

ermin=min(error);

for s=1:length(alpha)

if ermin==error(s)

alph_opt(t)=alpha(s);

end

end

step(t)=h;

%Рисуем график зависимости ошибки численного

%решения от параметра alpha

subplot(1,2,1);

semilogx(alpha,error,'LineWidth',0.75*t);

hold on

end

%Рисуем график зависимости оптимального значения

%параметра регуляризации alph_opt от шага сетки

subplot(1,2,2); plot(step,alph_opt);

%Определяем функцию Q(xi,eta), заданную в (58')

function y=Q(xi,eta)

if (xi==0)&(eta==0)

y=1;

else

y=(exp(xi+eta)-1)/(xi+eta);

end

%Определяем функцию f(xi), заданную в (58')

function y=f(xi)

global N h

%Используем формулу трапеции для аппроксимации

%интеграла, входящего в определение f(xi) в (58')

y=0.5*h*(fi(0,xi)+fi(1,xi));

for i=2:(N-1)

y=y+h*fi(h*(i-1),xi);

end

function y=fi(x,xi)

y=-exp(x*xi)*((x*(exp(x)+1))/(x^2+pi^2));

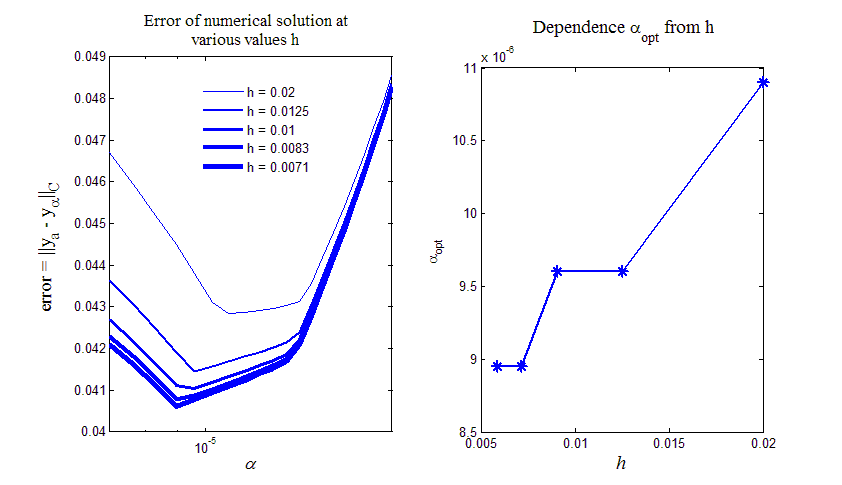
Рис.9. Изучение зависимости оптимального значения параметра регуляризации _opt от шага сетки h

На рис.9 приведен итог работы кода программы листинга_№9. На левом рисунке приведены пять графиков зависимости ошибки численного решения от параметра регуляризации  при различных значениях шага сетки h. На всех пяти графиках отчетливо видно наличие оптимального значения параметра регуляризации _opt, при котором ошибка численного решения error = (y_a = cos() — аналитическое решение исходной задачи (54), (57)) достигает минимального значения. На правом рисунке показана зависимость оптимального значения параметра регуляризации от шага сетки. Правый рисунок демонстрирует тенденцию стремления _opt к нулю при h  0, что иллюстрирует сходимость регуляризированного решения y_ к аналитическому решению y_a исходной задачи.

Некоторые приложения метода регуляризации. Некорректно поставленные задачи встречаются в практике довольно часто. Это, например, сглаживание и дифференцирование экспериментально измеренных функций, суммирование рядов Фурье с неточно заданными коэффициентами, решение линейных плохо обусловленных систем уравнений, решение задач оптимального управления, аналитическое продолжение функций, обратные задачи теплопроводности и геологической разведки, восстановление переданного сигнала и многие другие задачи.

Сглаживание функции. Пусть функция f(x), x  [a,b] измерена экспериментально и содержит заметную случайную ошибку. В терминах задачи (39) задача сглаживания функции f(x) состоит в решении некорректного уравнения , где . Применим метод регуляризации к данной задаче, ограничившись случаем n = 1, т.е. сильной регуляризацией. Тогда, принимая во внимание формулы (51) — (51), получим следующее уравнение Эйлера:

(62)

Согласно (62), сглаженная функция u(x) удовлетворяет линейному дифференциальному уравнению второго порядка, для которого поставлена вторая краевая задача.

Для решения уравнения (62) введем сетку по переменной x: x_i = a + (i  1)h, i = 1,…,N, h = (b  a)/(N  1) и составим разностную схему:

, (63)

где y_i  u(x_i), , i = 2,…,N  1. Недостающая пара уравнений вытекает из аппроксимации граничных условий со вторым порядком точности по шагу сетки:

. (64)

Находя значения в точках x = a и x = b из уравнения (62) и подставляя их в (64), получим следующие разностные уравнения для граничных условий:

, (65)

. (65)

На листинге_№10 приведен код программы сглаживания функции f(x) с помощью метода сильной регуляризации, который сводится к решению обыкновенного дифференциального уравнения второго порядка (62) согласно разностной схеме (63), (65), (65).