Листинг_№7
%Пример решения некорректного уравнения Фредгольма
%первого рода (54) с помощью метода регуляризации,
%т.е. путем сведения исходной задачи (54), (54') к
%решению корректного уравнения Фредгольма второго
%рода (55) с параметром регуляризации alpha > 0
function noncor
%Вводим число узлов сетки по переменным xi и eta
N=101; h=1.0/(N-1);
xi=0:h:1; eta=0:h:1;
%Определяем значения аналитического решения exp(xi)
%в узлах сетки xi
ya=exp(xi);
%Рисуем аналитическое решение пунктирной
%красной линией
subplot(1,2,1);
plot(xi,ya,'--','Color','red','LineWidth',4.5);
hold on
%Определяем набор параметров регуляризации alpha
alpha=[1e-2 1e-3 3e-4 1e-4 5e-5 1e-5];
%Организуем цикл расчетов с различными значениями
%параметра регуляризации
for s=1:length(alpha)
%Согласно разностной схеме (56) определяем
%линейную систему уравнений Ay = b относительно
%неизвестного вектора y
for i=1:N
A(i,1)=0.5*h*Q(xi(i),eta(1));
A(i,N)=0.5*h*Q(xi(i),eta(N));
for j=2:(N-1)
A(i,j)=h*Q(xi(i),eta(j));
end
A(i,i)=A(i,i)+alpha(s);
b(i)=f(xi(i));
end
%Решаем линейную систему уравнений Ay = b
y=A\b';
%Оцениваем ошибку численного решения y путем
%оценки разности error=||y-ya|| в норме C, где
%ya - аналитическое решение задачи (54), (54')
for i=1:N
z(i)=abs(y(i)-ya(i));
end
error(s)=max(z);
%Рисуем регуляризированные решения y при
%различных значениях параметра alpha
subplot(1,2,1); plot(xi,y,'LineWidth',3.5/s);
hold on
end
%Рисуем график зависимости ошибки численного
%решения от параметра alpha
subplot(1,2,2); loglog(alpha,error,'LineWidth',3);
%Определяем функцию Q(xi,eta), заданную в (55')
function y=Q(xi,eta)
if (xi==0)&(eta==0)
y=1;
else
y=(exp(xi+eta)-1)/(xi+eta);
end
%Определяем функцию f(xi), заданную в (55')
function y=f(xi)
%Используем формулу трапеции для аппроксимации
%интеграла, входящего в определение f(xi) в (55')
y=0.005*(fi(0,xi)+fi(1,xi));
for i=2:100
y=y+0.01*fi(0.01*(i-1),xi);
end
function y=fi(x,xi)
y=exp(x*xi)*((exp(x+1)-1)/(x+1));
На рис.7 приведен
итоговый график, генерируемый кодом
программы листинга_№7. На левом рисунке
приведены графики численного решения
при различных значениях регуляризирующего
значения. Видно, что как слишком большие
значения, так и слишком малые значения
приводят к большим отличиям от
аналитического решения
.
Аналитическое решение
представлено на левом рисунке в виде
красной жирной пунктирной линии. На
правом рисунке представлена зависимость
ошибки численного решения error
=
от параметра регуляризации
> 0. Из правого графика отчетливо видно
наличие оптимального значения параметра
opt
регуляризации, при котором ошибка
достигает минимума. В программе следующего
листинга_№8 будет изучена зависимость
оптимального значения параметра
регуляризации opt
от шага сетки h.
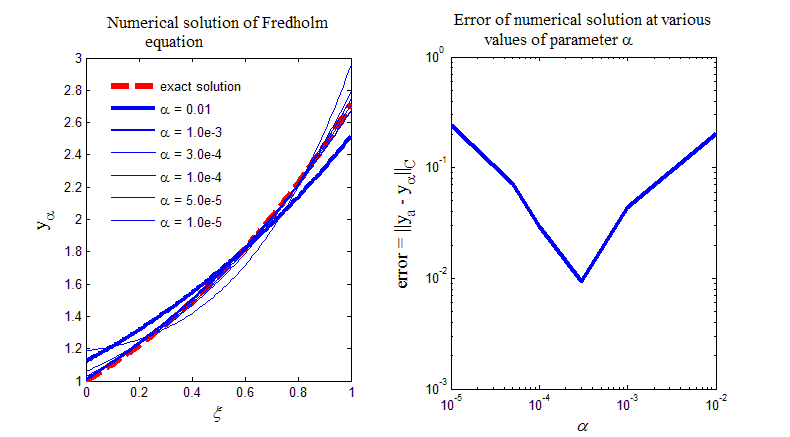
Рис.7. Численное решение некорректной задачи (54), (54) методом регуляризации, т.е. путем сведения ее к решению корректного уравнения Фредгольма второго рода (55)
На листинге_№8 приведено решение предыдущей некорректной задачи (54), (54) методом регуляризации с помощью решения корректного уравнения Фредгольма второго рода (55), (55). В этой программе нас будет интересовать зависимость оптимального значения параметра opt от шага сетки h. Напомним, что сетки были введены по переменным и для аппроксимации интеграла в интегральном уравнении (55) согласно разностной схеме (56). Необходимо убедиться, что при уменьшении шага сетки opt также уменьшается.
Листинг_№8
%На примере решения некорректного уравнения Фредгольма
%первого рода (54) с помощью метода регуляризации,
%т.е. путем сведения исходной задачи (54), (54') к
%решению корректного уравнения Фредгольма второго
%рода (55) исследуется зависимость оптимального
%значения параметра alpha_opt от шага сетки h
function noncor2
global N h
%Вводим начальное число узлов сетки по
%переменным xi и eta
N=21;
%Организуем цикл расчетов с разным сетками
for t=1:6
%Число узлов сетки по переменным xi и eta
%увеличиваем в арифметической прогрессии
N=N+20; h=1.0/(N-1);
xi=0:h:1; eta=0:h:1;
%Определяем значения аналитического решения exp(xi)
%в узлах сетки xi
ya=exp(xi);
%Определяем набор параметров регуляризации alpha
alph_l=1e-4; alph_r=1e-3; alph_h=(alph_r-alph_l)/20;
alpha=alph_l:alph_h:alph_r;
%Организуем цикл расчетов с различными значениями
%параметра регуляризации
for s=1:length(alpha)
%Согласно разностной схеме (56) определяем
%линейную систему уравнений Ay = b относительно
%неизвестного вектора y
for i=1:N
A(i,1)=0.5*h*Q(xi(i),eta(1));
A(i,N)=0.5*h*Q(xi(i),eta(N));
for j=2:(N-1)
A(i,j)=h*Q(xi(i),eta(j));
end
A(i,i)=A(i,i)+alpha(s);
b(i)=f(xi(i));
end
%Решаем линейную систему уравнений Ay = b
y=A\b';
%Оцениваем ошибку численного решения y путем
%оценки разности error=||y-ya|| в норме C, где
%ya - аналитическое решение задачи (54), (54')
for i=1:N
z(i)=abs(y(i)-ya(i));
end
error(s)=max(z);
end
%Определяем значение alph_opt, при котором ошибка
%численного решения минимальна
ermin=min(error);
for s=1:length(alpha)
if ermin==error(s)
alph_opt(t)=alpha(s);
end
end
step(t)=h;
%Рисуем график зависимости ошибки численного
%решения от параметра alpha
subplot(1,2,1);
loglog(alpha,error,'LineWidth',0.75*t);
hold on
end
%Рисуем график зависимости оптимального значения
%параметра регуляризации alph_opt от шага сетки
subplot(1,2,2); plot(step,alph_opt);
%Определяем функцию Q(xi,eta), заданную в (55')
function y=Q(xi,eta)
if (xi==0)&(eta==0)
y=1;
else
y=(exp(xi+eta)-1)/(xi+eta);
end
%Определяем функцию f(xi), заданную в (55')
function y=f(xi)
global N h
%Используем формулу трапеции для аппроксимации
%интеграла, входящего в определение f(xi) в (55')
y=0.5*h*(fi(0,xi)+fi(1,xi));
for i=2:(N-1)
y=y+h*fi(h*(i-1),xi);
end
function y=fi(x,xi)
y=exp(x*xi)*((exp(x+1)-1)/(x+1));
Рис.8. Изучение зависимости оптимального значения параметра регуляризации opt от шага сетки h
На рис.8 приведен итог работы кода программы листинга_№8. На левом рисунке приведены графики зависимости ошибки численного решения в зависимости от значений регуляризирующего параметра , полученные на различных сетках, т.е. при разных шагах h по переменным и . На всех шести графиках отмечается наличие оптимального значения параметра регуляризации opt. На правом графике построен профиль зависимости opt от шага сетки h. Видно, что оптимальное значение параметра регуляризации стремится к нулю по мере стремления шага сетки к нулю.
Можно доказать еще ряд важных утверждений при n = 1. Во-первых, решение регуляризованное задачи (51) — (51) равномерно сходится к решению исходной задачи (39), во-вторых, метод регуляризации при n = 1 обеспечивает сильную регуляризацию. Приведем лишь формулировки соответствующих теорем, опуская доказательства (формулировки и доказательства данных теорем приведены в учебнике5).
Теорема
№2. Пусть
,
тогда при n
= 1 и положительном
0 решение
задачи (51) — (51),
соответствующее правой части
,
равномерно сходится к
.
Теорема
№3. Метод регуляризации (41),
(42) при n
= 1 обеспечивает сильную регуляризацию,
т.е. регуляризованное решение сходится
к искомому решению в норме
.
Более подробно рассмотрим случай n = 1 на примере решения задачи (54) с ядром и правой частью вида:
. (57)
Задаче (54), (57) соответствует аналитическое решение u() = cos().
Согласно (51), (51), имеем (p0() 1, p1() 1):
, (58)
где функции Q(,), () с учетом (51), (57) имеют следующий вид:
. (58)
Для решения задачи (58), (58) введем сетки по переменным и : i = h(i 1), j = h(j 1), h = 1/(N 1), i,j = 1,2,…,N. Интеграл, входящий в (58), аппроксимируем по формуле трапеции, тогда
(59)
где yi u(i), i = 2,…,N. Недостающие два уравнения находятся из граничных условий, которые аппроксимируем со вторым порядком по h, т.е.
(60)
Находя соответствующие
из уравнения (58) и подставляя в (60), получим
граничные условия в следующем виде:
(61)
(61)
На листинге_№9 приведен код программы решения некорректной задачи (54), (57) методом регуляризации, т.е. путем сведения исходной задачи к решению корректного интегро-дифференциального уравнения (58), (58). Как и в предыдущих двух программах, выбор параметра регуляризации определяется его оптимальным значением opt, на котором реализуется минимум ошибки численного решения (при условии, конечно, что решение известно). В программе листинга_№9 исследуется зависимость оптимального значения параметра регуляризации opt от шага сетки h.