Листинг_№6

%Программа решения уравнения Фредгольма (30)

%путем замены ядра на вырожденное ядро (32), (33)

function degen_kernel

%Определяем параметр lambda, исходное число

%членов в разложении в ряд Фурье ядра, а также

%число расчетов с разным числом учтенных

%слагаемых в разложении ядра в ряд Фурье (32)

lambda=1; N=4; lmax=8;

%Определяем габариты области интегрирования

a=-1; b=1;

%Определяем число узлов сетки по аргументу x и xi

Nint=51; h=(b-a)/(Nint-1);

%Определяем сетки по x и xi

x=a:h:b; xi=a:h:b;

%Организуем цикл расчетов с разным числом учтенных

%слагаемых в разложении ядра в ряд Фурье (32)

for l=1:lmax

%Увеличиваем число слагаемых в разложении

%на единицу

N=N+1;

%Определяем систему линейных уравнений (30) в

%виде C alpha = d

for n=1:N

for m=1:N

I=0.5*B(n,xi(1))*A(m,xi(1))+...

0.5*B(n,xi(Nint))*A(m,xi(Nint));

for k=2:(Nint-1)

I=I+B(n,xi(k))*A(m,xi(k));

end

C(n,m)=-lambda*h*I;

if n==m

C(n,m)=C(n,m)+1;

end

end

I=0.5*B(n,xi(1))*f(xi(1))+...

0.5*B(n,xi(Nint))*f(xi(Nint));

for k=2:(Nint-1)

I=I+B(n,xi(k))*f(xi(k));

end

d(n)=h*I;

end

%Решаем систему уравнений C alpha = d

alpha=C\d';

%Определяем решение y по формуле (28)

for k=1:Nint

s=0;

for n=1:N

s=s+alpha(n)*A(n,x(k));

end

y(l,k)=f(x(k))+lambda*s;

end

end

%Рисуем численное решение исходного интегрального

%уравнения с максимальным числом учтенных

%слагаемых в разложении ядра в ряд Фурье

subplot(1,2,1); plot(x,y(lmax,:));

%Находим разницу между последующей и предыдущей

%итерациями в норме C

for l=1:(lmax-1)

for k=1:Nint

z(k)=abs(y(l+1)-y(l));

end

er(l)=max(z);

end

%Рисуем динамику разности последующей и

%предыдущих итераций в норме C от N -

%числа учтенных слагаемых в разложении (32)

subplot(1,2,2); semilogy(1:(lmax-1),er);

%Определяем функцию A(n,x)

function y=A(n,x)

if n==1

if x==0

y=1;

else

y=sin(x)/x;

end

else

y=((-1)^(n-1)*2*x*sin(x))/...

(x^2-(pi*(n-1))^2);

end

%Определяем функцию B(n,xi)

function y=B(n,xi)

if n==1

y=1;

else

y=cos(pi*(n-1)*xi);

end

%Определяем правую часть интегрального уравнения

function y=f(x)

y=sin(pi*x^2);

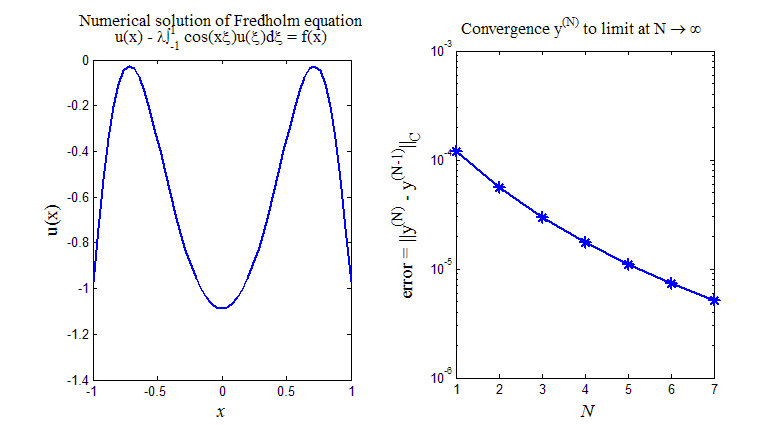
Рис.6. Численное решение уравнения Фредгольма (30) путем замены ядра уравнения на вырожденное ядро(32)

На рис.6 приведен итог работы кода программы листинга_№6. На левом рисунке приведено численное решение интегрального уравнения Фредгольма (30) методом замены ядра на вырожденное ядро (32), полученное путем разложения исходного ядра в ряд Фурье с последующим отбрасыванием бесконечного хвоста разложения. Расчетов проводилось несколько с различным числом оставленных слагаемых N в разложении (32). Численное решение y^(N) уравнения (33), полученное при некотором N сравнивалось с предыдущим, т.е. с y^(N 1) на предмет сходимости к некоторому пределу при N  . На правом рисунке приведена зависимость ошибки error = от числа учтенных слагаемых N. Можно наблюдать довольно быстрое стремление ошибки к нулю и соответственно сходимость численного y^(N) решения к некоторому пределу при N  .