Листинг_№4
%Программа численного решения уравнения
%Вольтерра (17) по разностной схеме (19)
function volterra
%Определяем отрезок интегрирования [a,b] и
%начальное значение для числа узлов сетки
a=0; b=1; N=4;
%Определяем цикл расчетов с разными сетками
for s=1:8
N=N+6; h=(b-a)/(N-1);
%Определяем сетки по x и xi
x=a:h:b; xi=a:h:b;
%Вычисляем значения искомого решения
%согласно формулам (19)
y(1)=f(x(1));
y(2)=f(x(2))-0.5*h*sinh(x(2)-xi(1))*y(1);
for n=3:N
I=0;
for m=2:(n-1)
I=I+sinh(x(n)-xi(m))*y(m);
end
y(n)=f(x(n))-0.5*h*sinh(x(n)-xi(1))*y(1)-h*I;
end
%Рисуем полученное решение
plot(x,y,'LineWidth',(2*s-1)/s);
hold on
end
%Определяем правую часть уравнения (17)
function y=f(x)
y=sin(2*pi*x)^2;
На рис.4 приведен итоговый график работы кода программы листинга_№4. Расчеты проводились на серии все более сгущающихся сетках. Отчетливо видно, что численное решение, по мере измельчение шага сетки, сходится к решению уравнения Вольтерра. Сходимость иллюстрируется увеличивающейся толщиной линией изображающей численное решение для все более подробных сеток.
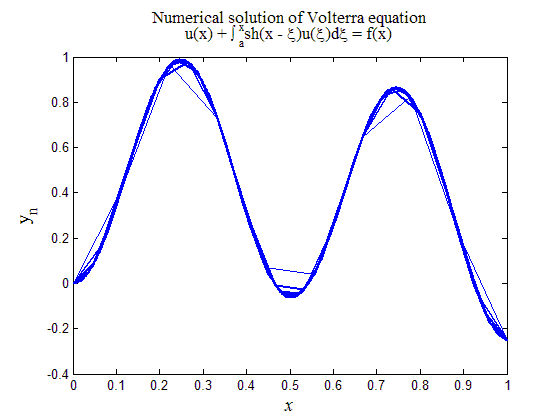
Рис.4. Численное решение уравнения Вольтерра (17) с помощью разностной схемы (19)
Метод последовательных приближений. Для неоднородного уравнения Фредгольма второго рода (3) запишем итерационный процесс:
, (20)
где s = 0,1,2,…, u0(x) = 0 — нулевое начальное распределение для решения u. Покажем, что при ограниченном ядре и достаточно малом значении || итерационный процесс сходится к решению уравнения (3).
Доказательство. Определим погрешность s-й итерации через zs = us(x) u(x). Вычитая (3) из (20), найдем
. (21)
Согласно (21), можно получить следующую оценку:
, (22)
где
.
Таким образом, согласно (22), итерации
при q
< 1 сходятся равномерно по x,
причем сходимость линейная. Последнее
неравенство всегда можно обеспечить,
выбирая достаточно малым параметр .
Метод последовательных приближений для уравнения Вольтерра (4) сходится равномерно по x при любых значениях параметра . Рассуждая аналогично предыдущему случаю, можно записать
. (23)
Проводя рассуждения, аналогичные доказательству сходимости метода Пикара (8.6) — (8.10), получим оценку
. (24)
При s правая часть неравенства (24) стремится к нулю при любых значениях параметра , что и доказывает наше утверждение.
Для примера рассмотрим численное решение уравнения Вольтерра (17) методом последовательных приближений, следуя формуле
(25)
Аппроксимируя интеграл, входящий в (25), по формуле трапеции, получим следующую расчетную схему:
(26)
На листинге_№5
приведен код программы, в которой
решается уравнение Вольтерра (17) методом
последовательных приближений в форме
(25), (26). Итерационный процесс прерывался
при условии, что
,
где
> 0 — параметр точности сходимости
итераций.
Листинг_№5
%Программа численного решения уравнения
%Вольтерра (17) методом последовательных
%приближений согласно уравнению (25)
function volt_iter
%Определяем точность сходимости итераций eps и
%максимальное число итераций itmax
eps=1e-6; itmax=10;
%Определяем отрезок интегрирования [a,b]
a=0; b=1;
%Определяем число узлов в сетке и шаг сетки
N=101; h=(b-a)/(N-1);
%Определяем сетки по x и xi
x=a:h:b; xi=a:h:b;
%Определяем параметры итерационного процесса
er=1; iter=0;
%Рисуем начальную итерацию u0(x)=0 пунктирной
%линией
y=zeros(1,N); plot(x,y,'--');
hold on
%Организуем цикл итераций
while (er>eps)&(iter<itmax)
%Вычисляем значения y2 для s+1 итерации
%согласно формулам (26)
y2(1)=f(x(1));
y2(2)=f(x(2))-0.5*h*sinh(x(2)-xi(1))*y(1);
for n=3:N
I=0;
for m=2:(n-1)
I=I+sinh(x(n)-xi(m))*y(m);
end
y2(n)=f(x(n))-0.5*h*sinh(x(n)-xi(1))*y(1)-h*I;
end
%Оцениваем разницу s+1-й и s-й итераций в норме C
for n=1:N
z(n)=abs(y2(n)-y(n));
end
er=max(z);
iter=iter+1;
y=y2;
%Рисуем полученное решение
plot(x,y,'LineWidth',(3*iter-1)/iter);
hold on
end
%Выводим число итераций и ошибку er=||y(s+1) - y(s)||c
[iter er]
%Определяем правую часть уравнения (17)
function y=f(x)
y=sin(2*pi*x)^2;
На рис.5 приведен итог работы кода программы листинга_№5. Было осуществлено численное решение уравнения Вольтерра (17) методом последовательных приближений согласно расчетной формуле (26). Расчеты показали, что достаточно 6 итераций для достижения точности сходимости = 106. На рис.5 пунктирной линией обозначена нулевая итерация u0(x) = 0. Последующие итерации представлены линиями с все большей толщиной и, начиная с третьей итерации, в имеющемся масштабе линии уже не различаются. Таким образом, метод последовательных итераций является весьма эффективным для решения уравнений Вольтерра второго рода.
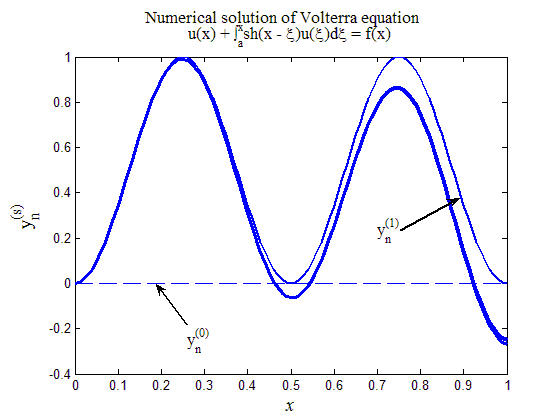
Рис.5. Численное решение уравнения Вольтерра (17) с помощью метода последовательных приближений (25), (26)
Метод замены ядра вырожденным. Ядро уравнения Фредгольма называется вырожденным, если оно может быть представлено в виде конечной суммы
. (27)
Решение уравнения Фредгольма с вырожденным ядром (27) осуществляется за конечное число шагов. Покажем это. Подставим ядро (27) в уравнение Фредгольма (3), тогда получим
, (28)
где
. (29)
Подставляя (28) в (29), найдем систему N линейных уравнений для нахождения коэффициентов 1,…,N:
. (30)
Из (28) — (30) следует, что вырожденное ядро (27) имеет ровно N собственных значений.
В качестве численного примера рассмотрим решение уравнения Фредгольма, имеющего следующий вид:
. (30)
Ядро K(x,) уравнения (30) может быть разложено в ряд Фурье по переменной :
. (31)
Рассмотрим теперь ограниченный отрезок ряда (31), отбросив бесконечный остаток, т.е. перейдем от ядра K(x,) к вырожденному ядру
. (32)
Заменяя в уравнении
(30) ядро K(x,)
= cos(x)
на вырожденное ядро
,
представленное в (32), получим уравнение
относительно неизвестной функции y(x):
. (33)
Изучим сходимость решения y(x) уравнения (33) к некоторому пределу при N путем решения системы линейных алгебраических уравнений (30) и восстановления решения по формуле (28). В этом случае можно считать, что
(34)
На листинге_№6 приведен код программы решения интегрального уравнения (30) путем замены ядра cos(x) на вырожденное ядро (32), полученное путем разложения ядра в ряд Фурье с последующим отбрасыванием бесконечного хвоста. Интегралы, входящие в (30), оценивались по формуле трапеции.