Листинг_№2

%Программа поиска собственного значения для

%однородного уравнения Фредгольма (5) согласно

%разностной схеме (12)

clear all

%Определяем отрезок интегрирования [a,b] и

%начальное значение для числа узлов сетки

a=0; b=1; N=4;

%Определяем цикл удвоения числа узлов сетки

for s=1:7

N=2*N; h=(b-a)/(N-1);

%Определяем сетки по x и xi

x=a:h:b; xi=a:h:b;

%Формируем матрицу левой части уравнения (12)

for n=1:N

A(n,1)=0.5*h*x(n)*xi(1);

for m=2:(N-1)

A(n,m)=h*x(n)*xi(m);

end

A(n,N)=0.5*h*x(n)*xi(N);

end

%Оцениваем численно собственное значение

lambda=1/max(eig(A));

%Численную ошибку оценки собственного значения

%делим на квадрат шага сетки

const(s)=abs((3.0/(b^3-a^3))-lambda)/h^2;

step(s)=h;

end

%Рисуем зависимость предстепенной константы от

%шага сетки

semilogx(step,const);

На рис.2 приведен итог работы кода программы листинга_№2. График изображает зависимость величины const в оценке ошибки приближенно вычисленного собственного значения  от шага сетки h. Из графика видно, что при шаге сетки, стремящемся к нулю, величина const действительно выходит на некоторое постоянное значение, т.е. разностная схема (12) обеспечивает второй порядок аппроксимации в оценке неизвестного собственного значения. Это не удивительно, т.к. формула трапеции, используемая при аппроксимации интеграла, имеет, как известно, второй порядок точности.

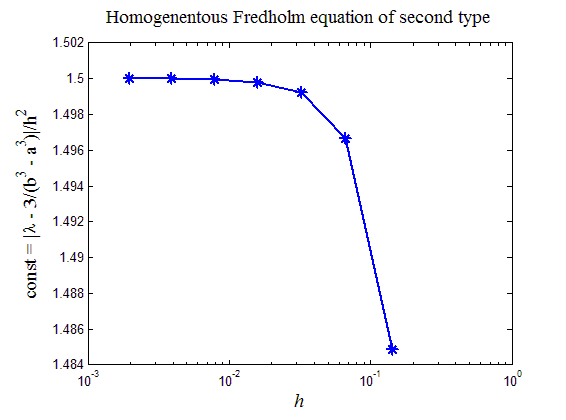
Рис.2. Оценка скорости сходимости численно найденного собственного значения однородного уравнения Фредгольма второго рода к точному собственному значению

Учитывая аппроксимацию интеграла (10), для неоднородного уравнения Фредгольма второго рода (3) можно записать следующую разностную схему:

. (13)

Система уравнений (13) легко может быть решена методом исключения Гаусса, когда   _i, i = 1,…,N, где _i, i = 1,…,N — собственные значения конечно-разностной задачи для соответствующего однородного уравнения Фредгольма второго рода. Обычно собственные значения ядра неизвестны. Поэтому для обнаружения и исключения случая   _i, i = 1,…,N, расчеты следует проводить на последовательности сгущающихся сеток. Если при сгущении сетки y_n сходится к некоторому решению u(x), то это и есть искомое решение. Если на одной из сеток расчет выпадает из общей закономерности, то имело место случайное совпадение   _i. Если на всех сетках решение y_n не сходится к пределу при h  0, то   _i.

Рассмотрим пример численного решения уравнения³

, (14)

которое имеет точное, но довольно громоздкое решение. Аппроксимируем интеграл в (14) по формуле трапеции, тогда получим следующую разностную схему:

, (15)

где n = 1,…,N. На листинге_№3 приведен код программы численного решения уравнения (14) по разностной схеме (15).

Листинг_№3

%Программа численного решения уравнения Фредгольма

%второго рода специального вида (14) по разностной

%схеме (15)

function fredh2

%Определяем константу lambda

lambda=-2;

%Определяем отрезок интегрирования [a,b] и

%начальное значение для числа узлов сетки

a=0; b=1; N=2;

%Определяем цикл расчетов с разными сетками

for s=1:9

N=N+3; h=(b-a)/(N-1);

%Определяем сетки по x и xi

x=a:h:b; xi=a:h:b;

%Формируем матрицу левой части уравнения (15)

for n=1:N

A(n,1)=0.5*h*lambda*abs(x(n)-xi(1));

for m=2:(N-1)

A(n,m)=h*lambda*abs(x(n)-xi(m));

end

A(n,N)=0.5*h*lambda*abs(x(n)-xi(N));

A(n,n)=A(n,n)+1;

end

%Определяем правую часть уравнения (15)

for n=1:N

F(n)=f(x(n));

end

%Решаем систему уравнений (15)

y=A\F';

%Рисуем полученное решение

plot(x,y,'LineWidth',(2*s-1)/s);

hold on

end

%Определяем правую часть уравнения (14)

function y=f(x)

y=sin(pi*x)^4;

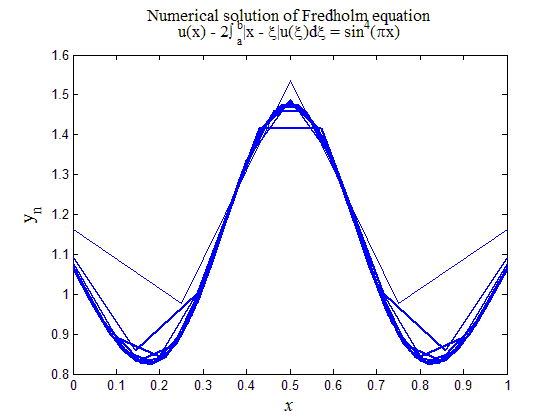
Рис.3. Численное решение уравнения Фредгольма второго рода (14) по разностной схеме (15)

На рис.3 приведен итог работы кода программы листинга_№3. Расчеты проводились на различных все более сгущающихся сетках. Это отражено на рис.3 в виде все более утолщающихся линиях на все более подробных сетках. Видно, что численное решение y_n сходится к некоторому решению по мере измельчения шага сетки h, т.е. выбранное значение  = 2 не является собственным значением ядра уравнения (14).

Уравнение Вольтерра (4) получается из уравнения Фредгольма (3) путем учета того, что K(x,) = 0 при x < . В этом случае алгебраическую систему уравнений (13) можно переписать в виде:

. (16)

Система уравнений (16) решается обратным ходом метода Гаусса, поскольку обращаемая матрица является нижней треугольной.

Рассмотрим пример решения уравнения Вольтерра (4) по разностной схеме на примере решения уравнения

, (17)

которое, согласно⁴, имеет аналитическое решение

. (18)

Как и выше воспользуемся квадратурной формулой трапеции, тогда разностная схема для решения уравнения (17) предстанет в виде:

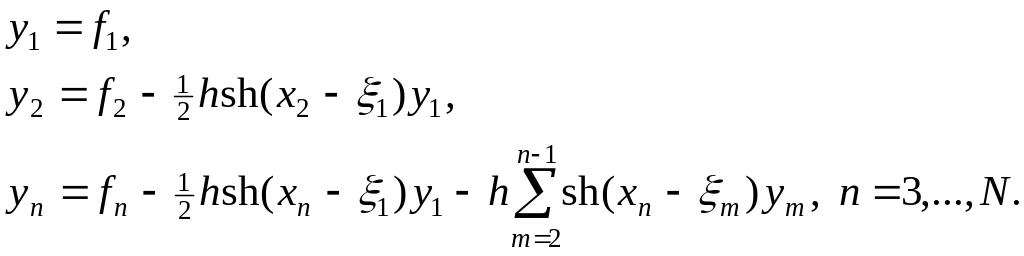(19)

На листинге_№4 приведен код программы численного решения уравнения Вольтерра (17) с помощью разностной схемы (19).