
Листинг_№11
%Изучение процедуры численного дифференцирования
%функции f(x) с точки зрения метода регуляризации
%путем решения интегро-дифференциального уравнения
%(68) по разностной схеме (69), (70), (70')
function different
global a b N h f
%Определяем габариты области решения
a=0; b=1;
%Определяем число узлов и шаг разностной схемы
N=101; h=(b-a)/(N-1);
%Определяем сетки по xi и eta
xi=a:h:b; eta=a:h:b;
%Определяем функцию, производную которой
%необходимо найти
f=sin(pi*xi);
%Накладываем на функцию f(x) небольшое зашумление
for i=1:N
f(i)=f(i)+0.05*randn;
end
%Определяем производную незашумленной функции
ya=pi*cos(pi*xi);
%Рисуем толстой пунктирной линией производную
%незашумленной функции f(x)
subplot(1,2,1);
plot(xi,ya,'--','Color','red','LineWidth',4);
hold on
%Определяем перечень значений параметра регуляризации
alpha=[2e-4 1e-4 3e-5 1e-5 5e-6 2e-6];
%Организуем цикл расчетов с разными значениями
%параметра регуляризации
for s=1:length(alpha)
%Учитываем левое граничное условие (70)
A=zeros(N,N);
A(1,1)=alpha(s)*(p1(xi(1))+0.5*h^2*p0(xi(1)));
A(1,2)=-alpha(s)*p1(xi(1));
A(1,1)=A(1,1)+0.25*h^3*(b-a);
for j=2:(N-1)
A(1,j)=A(1,j)+0.5*h^3*(b-eta(j));
end
d(1)=0.5*h^2*fi(1);
%Учитываем разностную схему (69)
for i=2:(N-1)
A(i,i-1)=-alpha(s)*p1(xi(i)-0.5*h);
A(i,i)=alpha(s)*(p1(xi(i)+0.5*h)+...
p1(xi(i)-0.5*h)+h^2*p0(xi(i)));
A(i,i+1)=-alpha(s)*p1(xi(i)+0.5*h);
A(i,1)=A(i,1)+0.5*h^3*(b-xi(i));
if i>2
for j=2:(i-1)
A(i,j)=A(i,j)+h^3*(b-xi(i));
end
end
A(i,i)=A(i,i)+0.5*h^3*(b-xi(i));
A(i,i)=A(i,i)+0.5*h^3*(b-eta(i));
if i<(N-1)
for j=(i+1):(N-1)
A(i,j)=A(i,j)+h^3*(b-eta(j));
end
end
d(i)=h^2*fi(i);
end
%Учитываем правое граничное условие
A(N,N-1)=p1(xi(N));
A(N,N)=-p1(xi(N))-0.5*h^2*p0(xi(N));
d(N)=0;
%Решаем линейную систему уравнений Ay=d
y=A\d';
%Рисуем полученные численные производные
%зашумленной функции f(x) при различных
%значениях параметра регуляризации
subplot(1,2,1); plot(xi,y,'LineWidth',s/2.5);
hold on
%Оцениваем ошибку численного дифференцирования
%зашумленной функции в норме C
for i=1:N
z(i)=abs(y(i)-ya(i));
end
error(s)=max(z);
end
%Рисуем график зависимости ошибки численного
%дифференцирования методом регуляризации от
%параметра регуляризации
subplot(1,2,2); semilogx(alpha,error);
%Определяем функцию p0(xi)
function y=p0(xi)
y=1+xi;
%Определяем функцию p1(xi)
function y=p1(xi)
y=1+xi^2;
%Определяем функцию fi(xi(i)), которая
%определена в (67)
function y=fi(i)
global a b N h f
if i==N
y=0;
end
if i==(N-1)
y=0.5*h*(f(N-1)+f(N)-2*f(1));
end
if i<(N-1)
y=0.5*h*(f(i)+f(N)-2*f(1));
for j=(i+1):(N-1)
y=y+h*(f(j)-f(1));
end
end
На рис.11 приведен вариант работы кода программы листинга_№11. На левом рисунке приведены шесть профилей численного решения y, полученных при шести значениях параметра регуляризации . Видно, что метод сильной регуляризации осуществляет процедуру дифференцирования корректно. Это выражается в сглаживании коротковолновых возмущений, привнесенных зашумленностью (x). На правом рисунке приведен график зависимости ошибки численного решения от параметра регуляризации . Видно, что параметр регуляризации имеет оптимальное значение opt, при котором ошибка является минимальной.
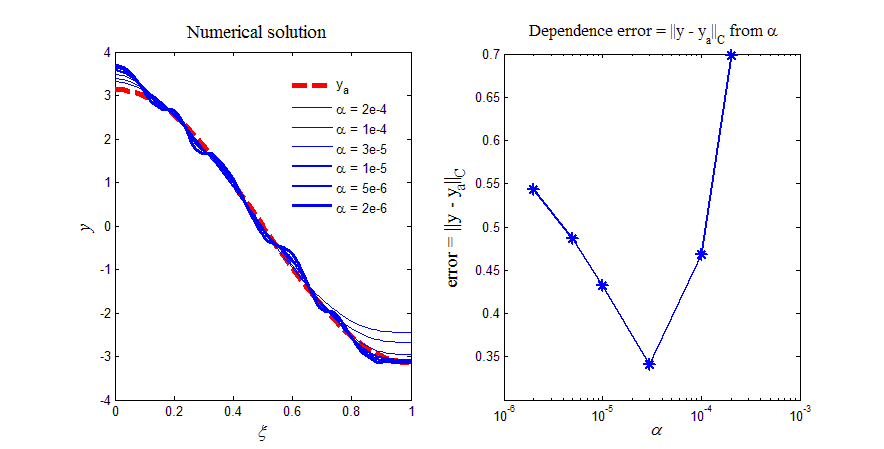
Рис.11. Изучение процедуры дифференцирования с помощью метода сильной регуляризации (68) — (70)
1 http://eqworld.ipmnet.ru/ru/solutions/ie/ie-toc6.htm
2 Михлин С.Г. Лекции по линейным интегральным уравнениям. — М.: Физматгиз, 1959.
3 http://eqworld.ipmnet.ru/en/solutions/ie/ie0402.pdf
4 http://eqworld.ipmnet.ru/en/solutions/ie/ie0212.pdf
Пространство C(p)
— пространство функций u(),
a <
< b, непрерывных и
ограниченных вместе со своими p-ми
производными, причем
![]() .
.
5 Калиткин Н.Н. Численные методы. — М.: Наука, Главн. ред. физ.-мат. литературы, 1978, с.471 — 473.
—
