Плохотников К.Э. ВЫЧИСЛИТЕЛЬНЫЕ МЕТОДЫ. Теория и практика в среде MATLAB

Лекция №14 Интегральные уравнения Корректно поставленные задачи

Постановка задачи. Интегральным называют уравнение, в котором неизвестная функция u(x) входит под знак интеграла. В одномерном случае интегральное уравнение имеет следующий вид:

, (1)

где ядро K(x,,u) и правая часть F(x,u) считаются заданными функциями. Среди нелинейных интегральных уравнений общего вида (1) различают нелинейные уравнения Урысона и Гоммерштейна:

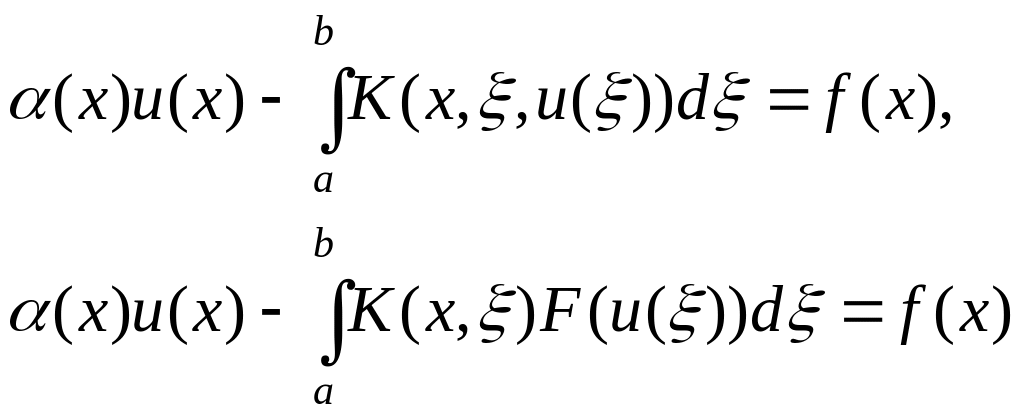
соответственно.

В качестве примера интегрального уравнения можно привести задачу восстановления переданного радиосигнала u(t) по принятому сигналу f(t) согласно решению интегрального уравнения типа свертки:

. (2)

В (2) ядро K() определяется свойствами приемной аппаратуры и окружающей сигнал среды.

Отметим то обстоятельство, что уравнения в частных производных часто являются следствием законов сохранения, которые могут выступать в форме интегральных уравнений. Например, уравнения Навье-Стокса, используемые для описания сплошной среды, являются следствием законов сохранения массы, импульса и энергии плюс соответствующих условий гладкости, наложенных на неизвестные величины. Данное обстоятельство было неоднократно использовано в предыдущих лекциях при построении консервативных разностных схем.

Если переход от обыкновенных дифференциальных уравнений к уравнениям в частных производных является принципиальным усложнением, переход в интегральном уравнении к многомерному случаю естественен и состоит в формальной замене в (1) переменных x и  на соответствующие векторы x = (x₁,…,x_p)  G,  = (₁,…,_p)  G и проведении интегрирования по области G.

В дальнейшем рассмотрим некоторые частные случаи одномерного уравнения (1).

Наиболее хорошо изучены линейные интегральные уравнения, когда неизвестная функция u входит в интегральное уравнение линейно. Например, линейное уравнение

, (3)

называют уравнением Фредгольма второго рода. Если ядро K(x,) = 0 при x < , т.е. ядро отлично от нуля на треугольной области, то уравнение (3) переходит в уравнение, которое принято называть уравнением Вольтерра второго рода:

. (4)

Если в уравнениях (3), (4) отбросить член u не входящий под знак интеграла, то получим уравнения Фредгольма и Вольтерра первого рода. Уравнения первого рода являются некорректно поставленными и будут рассмотрены далее специально. Уравнения второго рода являются корректными. Рассмотрим их более подробно.

Для однородного уравнения Фредгольма второго рода (3) ставится задача на собственные значения:

. (5)

Задача на собственные значения (5) состоит в поиске таких  = _i, при которых уравнение (5) имеет нетривиальные решения u = _i. В этом случае _i называются собственными значениями ядра K(x,), а _i — его собственными функциями. Если ядро вещественное и симметричное, т.е. K(x,) = K(,x) = K^*(x,), то оно имеет, по крайней мере, одно собственное значение. Все собственные значения такого ядра вещественны, а его собственные функции ортогональны друг другу. Отметим, что система функций _i может быть неполной и даже конечной.

Неоднородное уравнение Фредгольма (3) при значении параметра , отличного от любого из собственных значений _i ядра, имеет единственное решение u(x), которое для симметричного ядра может быть представлено в виде разложения Шмидта:

. (6)

Если ядро K(x,) и правая часть f(x) интегрируемы с квадратом, то ряд в (6) сходится абсолютно и равномерно. Из (6) видно, что при   _i решение u(x) существует, единственно и непрерывно зависит от f(x), т.е. задача (3) корректна. Если параметр  равен одному из собственных значений _i, тогда неоднородное уравнение Фредгольма (3) может не иметь решения или иметь их множество при специальном выборе правой части. Другими словами, при  = _i задача (3) является некорректно поставленной.

Уравнение Вольтерра не имеет собственных значений, поэтому неоднородное уравнение (4) всегда имеет единственное решение.

Разностный метод. Проиллюстрируем использование разностного метода на примере численного решения нелинейного интегрального уравнения

, (7)

взятого с сайта¹. Там же приведен аналитический метод решение уравнения (7), который дает пару решений:

. (7)

Введем сетки по переменным x и   [0,1]: x_n = h(n  1), n = 1,…,N, _m = hm, m = 1,…,N, h = 1/(N  1). Аппроксимируем интеграл в (7) по формуле трапеции и запишем уравнение (7) в узлах сетки, тогда, считая, что y_n  u(x_n), получим

. (8)

Нелинейную систему алгебраических уравнений (8) будем решать методом последовательных приближений по формуле

, (9)

где s = 2,3,… — номер итерации в методе последовательных приближений, а — произвольное начальное приближение.

На листинге_№1 приведен код программы численного решения интегрального уравнения (7) методом последовательных приближений согласно схеме (9). Процедура повтора итераций прекращалась согласно критерию: , где  > 0 — малый параметр точности, который находится в нашем распоряжении.