
Листинг_№9
%Программа численного решения задачи (62),
%(68), (72) попеременно-треугольным способом
function triangle
global a b k1 k2
%Определяем габариты области интегрирования и
%константы k1, k2, входящие в уравнение (62)
a=1; b=1; k1=1; k2=1;
%Определяем число узлов сетки и шаги h1, h2
%по переменным x1, x2
N=35; M=35;
h1=a/(N-1); h2=b/(M-1);
x1=0:h1:a; x2=0:h2:b;
%Определяем шаг в итерационной схеме на
%установление и число шагов на установление
tau=0.001; Nt=30;
r1=(tau*k1)/h1^2; r2=(tau*k2)/h2^2;
r3=1+r1+r2;
%Определяем начальное распределение
for n=1:N
for m=1:M
y(1,n,m)=0.1*randn;
end
end
%Определяем нижнее и верхнее граничные условия
for t=1:Nt
for n=1:N
y(t,n,1)=u(x1(n),x2(1));
y(t,n,M)=u(x1(n),x2(M));
end
end
%Определяем левое и правое граничные условия
for t=1:Nt
for m=1:M
y(t,1,m)=u(x1(1),x2(m));
y(t,N,m)=u(x1(N),x2(m));
end
end
%Оцениваем ошибку отличия численного решения от
%аналитического в норме C
for n=1:N
for m=1:M
z(n,m)=abs(y(1,n,m)-u(x1(n),x2(m)));
end
end
error(1)=max(max(z));
%Организуем основной цикл итераций на установление
for t=2:Nt
w=zeros(N,M);
%Находим промежуточное решение w согласно (71)
for m=2:(M-1)
for n=2:(N-1)
w(n,m)=(r1*w(n-1,m)+r2*w(n,m-1)+...
(k1/h1^2)*(y(t-1,n-1,m)-...
2*y(t-1,n,m)+y(t-1,n+1,m))+...
(k2/h2^2)*(y(t-1,n,m-1)-...
2*y(t-1,n,m)+y(t-1,n,m+1))+...
f(x1(n),x2(m)))/r3;
end
end
%Находим решение на следующем слое согласно (71')
for m=(M-1):-1:2
for n=(N-1):-1:2
y(t,n,m)=(r1*y(t,n+1,m)+r2*y(t,n,m+1)+...
y(t-1,n,m)+r1*(y(t-1,n,m)-...
y(t-1,n+1,m))+r2*(y(t-1,n,m)-...
y(t-1,n,m+1))+tau*w(n,m))/r3;
end
end
%Оцениваем ошибку отличия численного решения от
%аналитического в норме C
for n=1:N
for m=1:M
z(n,m)=abs(y(t,n,m)-u(x1(n),x2(m)));
end
end
error(t)=max(max(z));
end
for n=1:N
for m=1:M
z(n,m)=y(Nt,n,m);
end
end
%Рисуем профиль численного решения на последнем шаге
%итерации
subplot(1,2,1); surf(x2,x1,z);
%Рисуем профиль ошибки численного решения от номера
%шага итерации
subplot(1,2,2): plot(1:Nt,error);
%Определяем функцию правой части (68)
function y=f(x1,x2)
global a b k1 k2
y=-2*k2*(x1-0.5*a)^2-2*k1*(x2-0.5*b)^2;
%Определяем аналитическое решение (69)
function y=u(x1,x2)
global a b
y=(x1-0.5*a)^2*(x2-0.5*b)^2;
На рис.10 приведен
итог работы кода программы листинга_№9.
На левом рисунке приведен трехмерный
профиль численного решения по схеме
(71), (71)
задачи Дирихле (62), (68), (72) попеременно-треугольным
способом. Трехмерный профиль приведен
для численного решения полученного на
последнем шаге итерационного процесса,
это решение весьма близко к аналитическому
решению (69) исходной задачи. На правом
рисунке приведена зависимость ошибки
численного решения от номера шага
итерационного процесса, т.е. error
=
![]() ,
где t
= 1,…, tmax
— номер итерации.
,
где t
= 1,…, tmax
— номер итерации.
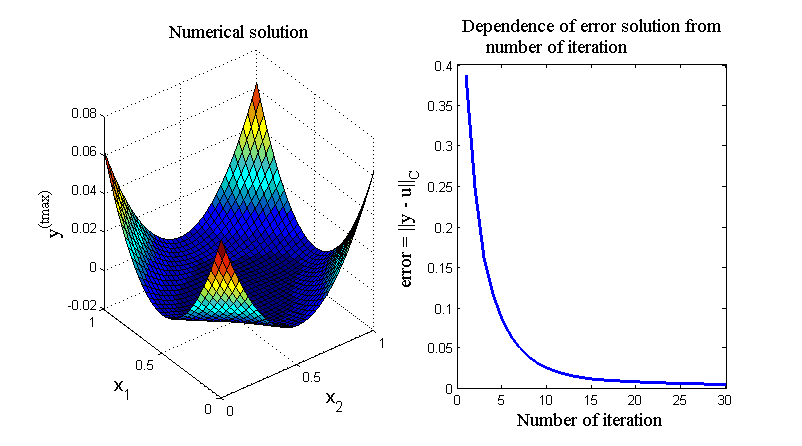
Рис.10. Решение задачи Дирихле (62), (68), (72) попеременно- треугольным способом
См., например: Тихонов А.Н., Самарский А.Н. Уравнения математической физики. — М.: Наука, Глав. ред. физ.-мат. литературы, 1972.
1 Калиткин Н.Н. Численные методы. — М.: Наука, Глав. ред. физ.-мат. литературы, 1978.
2 Более подробно о многочленах Чебышева в книге: Калиткин Н.Н. Численные методы. — М.: Наука, Глав. ред. физ.-мат. литературы, 1978 (Приложение, с.501).
3 Самарский А.А., Гулин А.В. Численные методы. — М.: Наука, Глав. ред. физ.-мат. литературы, 1989, с.317.
—
