Листинг_№7

%Программа решения уравнения (44) методом

%быстрого преобразования Фурье по схеме (52)

%с правой частью (53) в уравнении u''-mu u= -f

function fourier

global a mu h w

a=1; mu=1;

%Определяем возможные степени двойки числа

%узлов сетки N=2^r

r=[3 4 5 6 7 8];

%Организуем цикл расчетов с разными N=2^r

for i=1:length(r)

%Определяем параметры сетки и параметр w

N=2^r(i); h=a/N; x=0:h:a;

w=cos((2*pi)/N)+sqrt(-1)*sin((2*pi)/N);

%Вычисляем bp согласно схеме быстрого

%преобразования Фурье в (52)

for p=0:(N-1)

bp=0.5*(b(r(i),0,mod(p,2^(r(i)-1)))+...

b(r(i),1,mod(p,2^(r(i)-1)))*w^(-p));

afrr(p+1)=bp/((4/h^2)*sin((pi*p)/N)^2+mu);

end

%Находим решение согласно (45)

for n=0:N

s=0;

for q=0:(N-1)

s=s+afrr(q+1)*w^(n*q);

end

y(n+1)=s;

end

%Находим отклонение численного решения от

%аналитического, т.е. ошибку численного решения

%в норме C

for n=0:N

y(n+1)=abs(y(n+1)-x(n+1)^2*(a-x(n+1))^2);

end

error(i)=max(max(y));

Nr(i)=N;

end

%Рисуем график зависимости ошибки численного решения

%от числа шагов сетки в логарифмическом масштабе по

%осям абсцисс и ординат

loglog(Nr,error);

%Определяем функцию правой части

function y=f(x)

global a mu

y=-2*a^2+12*a*x+(mu*a^2-12)*x^2-2*mu*a*x^3+mu*x^4;

%Определяем рекурсивную функцию вычисления

%коэффициентов b(l1,l2,...,lk,pk) в быстром

%преобразовании Фурье согласно схеме (52)

function z=b(r,l,p)

global h w

k=length(l);

if k<=(r-2)

l0=[l 0]; l1=[l 1];

z=0.5*(b(r,l0,mod(p,2^(r-k)))+...

b(r,l1,mod(p,2^(r-k)))*w^(-2^k*p));

else

s=0;

for i=1:k

s=s+l(i)*2^(i-1);

end

z=0.5*(f(s*h)+f((s+2^(r-1))*h)*w^(-2^(r-1)*p));

end

На рис.7 приведен итоговый график работы кода программы листинга_№7. Из графика на рис.7 видно, что с экспоненциальный рост числа узлов сетки приводит к экспоненциальному уменьшению ошибки численного решения с помощью метода быстрого преобразования Фурье согласно схеме (52). Ошибка оценивалась по отношению к аналитическому решению (54) согласно формуле: error = .

Метод быстрого преобразования Фурье легко обобщается на многомерный случай. Для примера рассмотрим уравнение

,

для которого определена первая краевая задача в прямоугольной области. Введем равномерную сетку , n = 0,1,…,N, , m = 0,1,…,M и определим на ней разностную схему

(55)

Решение уравнения (55) будем искать в виде разложения Фурье:

.

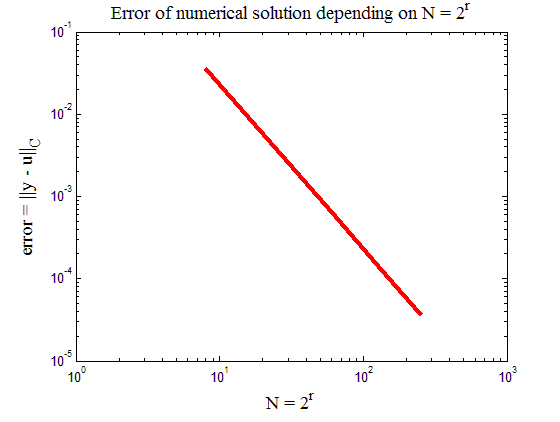
Рис.7. Зависимость ошибки численного решения задачи (44) с помощью быстрого преобразования Фурье (52) от N = 2^r

Аналогично формулам одномерного случая (46), (47) имеем

, (46)

где

. (47)

Представим (47) в следующем виде:

. (56)

Обе суммы в (56) имеют вид, аналогичный сумме (47). По этой причине, если N и M разлагаются на множители, то каждую из сумм можно вычислить согласно рекуррентным формулам типа (52). Если и , то число операций на каждый узел сетки есть O(r₁L₁ + r₂L₂) = O(log(NM)), что аналогично одномерному случаю.