Прямые методы решения

Стационарные (не эволюционные) схемы можно составлять непосредственно, аппроксимируя производные разностями, а также с помощью интегро-интерполяционного метода. Так для многомерного уравнения u =  f простейшая разностная схема имеет следующий вид:

. (43)

Для стационарных схем типа (43) наиболее сложным является вопрос о реальном вычислении решения. Действительно, разностная схема (43) имеет N^p неизвестных, если считать, что число узлов по каждому из направлений N. На листинге_№6 приведен код программы рисования матрицы двумерного уравнения (43). В программе используется специальная функция spy пакета MATLAB, которая предназначена для изображения разреженных матриц.

Листинг_№6

%Программа рисования структуры матрицы

%двумерного разностного уравнения (43)

clear all

%Выбираем число узлов сеток по x1 и x2

N=7; M=7;

%Создаем матрицу двумерного разностного

%уравнения (43), заполненную нулями

A=zeros(N*M);

%Вносим единицы в те места матрицы, которые

%отвечают уравнениям разностной схемы (43)

%для регулярных узлов

for m=2:(M-1)

for n=2:(N-1)

k=n+N*(m-1);

kn1=n-1+N*(m-1);

kn2=n+1+N*(m-1);

km1=n+N*(m-2);

km2=n+N*m;

A(k,k)=1;

A(k,kn1)=1; A(k,kn2)=1;

A(k,km1)=1; A(k,km2)=1;

end

end

%Рисуем матрицу A в координатах n и m

spy(A);

%Создаем матрицу B заполненную нулями для

%учета нерегулярных узлов, т.е. для учета

%возможных граничных условий

B=zeros(N*M);

%Формируем матрицу B, добавляя в нее единицы,

%учитывающие возможные ненулевые граничные

%условия

for n=1:N

B(n,n)=1; B(n,n+N)=1;

B(n+N*(M-1),n+N*(M-1))=1;

B(n+N*(M-1),n+N*(M-2))=1;

end

for m=1:M

B(1+N*(m-1),1+N*(m-1))=1;

B(1+N*(m-1),2+N*(m-1))=1;

B(N+N*(m-1),N+N*(m-1))=1;

B(N+N*(m-1),N-1+N*(m-1))=1;

end

hold on

%Добавляем образ граничных условий B к

%матрице A

spy(B,10);

Результат работы кода программы листинга_№6 приведен на рис.6, где изображена матрица двумерного уравнения (43). Матрица ленточная, причем лента не полностью заполнена и имеет ширину ~ N. Красным цветом выделены элементы матрицы, наличие которых отвечает заданию возможных граничных условий второго рода при x₁ = 0, x₁ = a и x₂ = 0, x₂ = b.

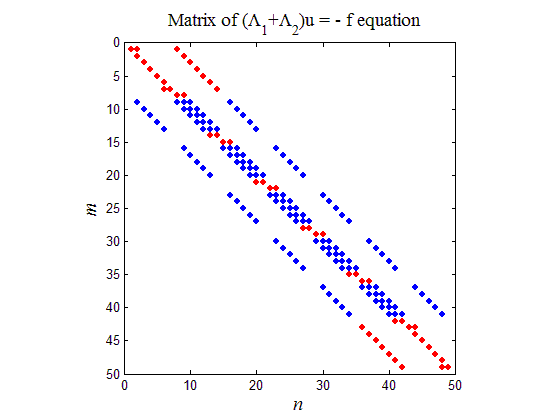
Рис.6. Матрица двумерного разностного уравнения (43)

Вычисление разностного решения методом Гаусса, который не учитывает разреженность матрицы, требует ~ N^3p операций (при p = 1 на метод прогонки уходит ~ N операций), т.е. на каждый узел сетки приходится ~ N^2p операций. При заметном значении N это число операций может оказаться неприемлемо большим. Это означает, что прямое решение двумерного разностного уравнения (43) методом Гаусса возможно при значениях N, не более 100.

Если строить схемы высокого порядка точности, например, с помощью сплайнов в комбинации с вариационными методами и использовать сгущающиеся сетки (обычно в последовательности N = 4, 8, 16, 32) с уточнением решения по способу Рунге, то может быть достигнута заметная точность даже при небольшом числе узлов сетки.

Рассмотрим некоторые способы прямого решения важных частных эллиптических задач. К ним относится быстрое преобразование Фурье, которое применимо к задаче Дирихле на прямоугольнике.

Быстрое преобразование Фурье основано на том, что, если N_ — число узлов сетки по переменной x_ разлагается на множители, то вычислять коэффициенты дискретного преобразования Фурье можно не по прямым формулам, а по более экономичным, рекуррентным формулам. При метод является особенно быстрым и требует ~ 4log₂N действий на каждый узел сетки.

Первоначально рассмотрим одномерную задачу для уравнения с постоянными коэффициентами . Аппроксимируем последнее уравнение на разностной схеме x_n = nh, n = 0,1,…,N:

. (44)

Разностное решение y_n будем искать в виде разложения Фурье:

, (45)

где . Подставим (45) в (44), умножим полученное уравнение на , просуммируем по n от 0 до N1. Учитывая условие ортогональности гармоник, найдем

, (46)

где величины

(47)

являются дискретными коэффициентами Фурье правой части уравнения. Разностное решение уравнения (44) может быть получено согласно формулам (45) — (47). Формулы (45) — (47) являются неэкономичными, поскольку надо вычислить N коэффициентов b_p, на вычисление каждого из которых требуется ~ 2N операций, т.е. всего ~ 2N² операций. Последний показатель заметно уступает методу прогонки, где требуется ~ N операций.

Пусть теперь число N можно разложить на сомножители, например, N = KL, тогда формулу (47) можно преобразовать таким образом, чтобы общее количество требуемых операций уменьшилось. Представим индексы n и p в виде:

(48)

С учетом представления (48) перепишем сумму (47) в виде двойной суммы:

. (49)

Поскольку , отбросим в (49) в показатели степени последнее слагаемое, тогда можно записать следующее представление

, (50)

где

. (51)

Проведем баланс числа операций по формулам (50), (51). Вычисление N коэффициентов b(p) по формуле (50) требует 2NL операций. Вычисление KL = N вспомогательных коэффициентов по формуле (51) требует дополнительно 2NK операций. Следовательно, всего операций для определения коэффициентов Фурье по формулам (50), (51) равно 2N(L + K), что существенно меньше 2N². Действительно, пусть , тогда требуется операций, что в раз меньше, чем 2N².

Если K может быть также разложено на множители, то формулу (51) можно преобразовать аналогично, что еще более уменьшит общее количество операций. Приведем без вывода рекуррентные формулы вычисления коэффициентов Фурье при N = L^r:

,

, (52)

,

при этом .

Число вспомогательных коэффициентов k-го ранга равно N, т.е., согласно (52), для вычисления коэффициентов всех рангов требуется 2NLr операций. Учитывая, что , можно найти оптимальное число сомножителей , при котором общее число операций 2NLr минимально. Приравнивая производную по r выражения к нулю, находим . Таким образом, минимум числа операций 2eNlnN реализуется, когда и при . Однако, в рамках процедуры быстрого преобразовании Фурье принято считать, что N = 2^r и L = 2. Данный случай мало отличается от оптимального, т.к. требуемое в этом случае число операций 4Nlog₂N мало отличается от оптимального числа операций  3,768 Nlog₂N.

На отрезке [0,a] с помощью процедуры (52) быстрого преобразования Фурье численно решим задачу , правая часть которой

(53)

обеспечивает аналитическое решение вида:

. (54)

На листинге_№7 приведен код программы решения задачи (44) методом быстрого преобразования Фурье по схеме (52) и сравнение полученного численного решения с аналитическим решением (54).