Листинг_№4
%Программа рисования набора чебышевских шагов
%(31) tau(k), k=1,2,...,K
clear all
%Определяем точность счета на установление
eps=1e-8;
%Определяем габариты области в плоскости x1 и x2
a=1; b=1;
%Определяем число узлов сеток по x1 и x2
N=101; M=301;
h1=a/(N-1); h2=b/(M-1);
%Пороговое значение шага, превышение которого
%приводит к неустойчивости при решении по
%разностной схеме (34)
tau0=(0.5*h1^2*h2^2)/(h1^2+h2^2);
%Определяем спектральные пределы оператора A
gm1=(4/h1^2)*sin((pi*h1)/(2*a))^2+...
(4/h2^2)*sin((pi*h2)/(2*b))^2;
gm2=(4/h1^2)*cos((pi*h1)/(2*a))^2+...
(4/h2^2)*cos((pi*h2)/(2*b))^2;
ro=(sqrt(gm2)-sqrt(gm1))/(sqrt(gm2)+sqrt(gm1));
%Определяем число шагов Чебышева K
K=fix(log(2/eps)/log(1/ro));
%Вычисляем шаги Чебышева
for k=1:K
tau(k)=2/((gm2+gm1)+...
(gm2-gm1)*cos((pi*(2*k-1))/(2*K)));
end
%Рисуем шаги Чебышева от номера k
semilogy(1:K,tau,'LineWidth',2);
hold on
%Рисуем линию, изображающую пороговое значение
%устойчивости разностной схемы (34)
semilogy(1:K,tau0*ones(1,K),'--',...
'LineWidth',3,'Color','red');
На рис.4 приведены значения шагов Чебышева при некотором выборе значений соответствующих параметров. Пунктирная линия на рис.4 обозначает порог устойчивости расчетов по разностной схеме (34). Видно, что приблизительно половина шагов из всего набора меньше порогового значения, а вторая половина больше.
Идея выбора определенной последовательности чебышевских шагов состоит в том, чтобы шаг роста неустойчивости был скомпенсирован на следующем шаге соответствующим ее уменьшением. Правило перестановки особенно просто, когда число шагов является степенью двойки. В этом случае шаги располагаем в естественном порядке и группируем парами: первый — последний, второй — предпоследний и т.д. Затем пары группируются в четверки: первая — последняя и т.д. Аналогично группируются восьмерки и т.д. Например, для 16 шагов искомый порядок таков:
{1, 16, 8, 9, 4, 13, 5, 12, 2, 15, 7, 10, 3, 14, 6, 11}. (38)
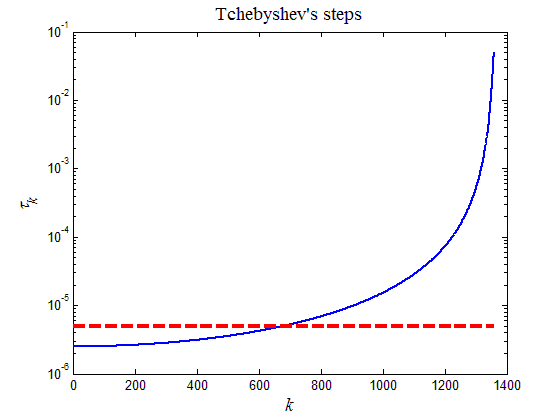
Рис.4. Чебышевский набор шагов при некотором выборе значений соответствующих параметров
Возвращаемся к разностной схеме (34). Будем считать, что
, (39)
тогда уравнение
(40)
имеет следующее решение
. (41)
Уравнение (40) будем решать с помощью счета на установление по разностной схеме (34) с правой частью (41) и с последовательностью чебышевских шагов (38). Будем оценивать динамику ошибки
errork
=
,
k
= 1,…,K
+ 1, (42)
где
— аналитическое решение (41). Код
соответствующей программы представлен
на листинге_№5.
Листинг_№5
%Программа оценки качества сходимости в схеме
%на установление (34) при специальном выборе
%последовательности чебышевских шагов
function cheb2
global a b
%Определяем точность счета на установление
eps=1e-2;
%Определяем габариты области в плоскости x1 и x2
a=1; b=1;
%Определяем число узлов сеток по x1 и x2
N=11; M=11;
h1=a/(N-1); h2=b/(M-1);
%Задаем сетки по x1 и x2
x1=0:h1:a; x2=0:h2:b;
%Определяем спектральные пределы оператора A
gm1=(4/h1^2)*sin((pi*h1)/(2*a))^2+...
(4/h2^2)*sin((pi*h2)/(2*b))^2;
gm2=(4/h1^2)*cos((pi*h1)/(2*a))^2+...
(4/h2^2)*cos((pi*h2)/(2*b))^2;
ro=(sqrt(gm2)-sqrt(gm1))/(sqrt(gm2)+sqrt(gm1));
%Определяем число шагов Чебышева K
K=fix(log(2/eps)/log(1/ro));
%Вычисляем шаги Чебышева
for k=1:K
tau(k)=2/((gm2+gm1)+...
(gm2-gm1)*cos((pi*(2*k-1))/(2*K)));
end
%Задаем порядок использования шагов Чебышева
ord=[1 16 8 9 4 13 5 12 2 15 7 10 3 14 6 11];
%Вычисляем аналитическое решение (41)
for n=1:N
for m=1:M
ya(n,m)=(x1(n)-0.5*a)^4+(x2(m)-0.5*b)^4;
end
end
%Определяем начальное условие для схемы (34)
for n=1:N
for m=1:M
y(1,n,m)=0;
end
end
%Задаем граничные условия при x2=0 и x2=b
for k=1:(K+1)
for n=1:N
y(k,n,1)=(x1(n)-0.5*a)^4+(x2(1)-0.5*b)^4;
y(k,n,M)=(x1(n)-0.5*a)^4+(x2(M)-0.5*b)^4;
end
end
%Задаем граничные условия при x1=0 и x1=a
for k=1:(K+1)
for m=1:M
y(k,1,m)=(x1(1)-0.5*a)^4+(x2(m)-0.5*b)^4;
y(k,N,m)=(x1(N)-0.5*a)^4+(x2(m)-0.5*b)^4;
end
end
%Определяем основной цикл расчета по схеме (34)
for k=2:(K+1)
p1=tau(ord(k-1))/h1^2; p2=tau(ord(k-1))/h2^2;
for n=2:(N-1)
for m=2:(M-1)
y(k,n,m)=y(k-1,n,m)+...
p1*(y(k-1,n-1,m)-2*y(k-1,n,m)+...
y(k-1,n+1,m))+p2*(y(k-1,n,m-1)-...
2*y(k-1,n,m)+y(k-1,n,m+1))+...
tau(ord(k-1))*f(x1(n),x2(m));
end
end
end
%Определяем величину ошибки (42) на
%каждом шаге расчетов
for k=1:(K+1)
for n=1:N
for m=1:M
z(n,m)=100*abs(y(k,n,m)-ya(n,m));
end
end
error(k)=max(max(z));
end
%Рисуем динамику ошибки от номера шага
semilogy(1:(K+1),error);
%Определяем функцию правой части (39)
function y=f(x1,x2)
global a b
y=-12*(x1-0.5*a)^2-12*(x2-0.5*b)^2;
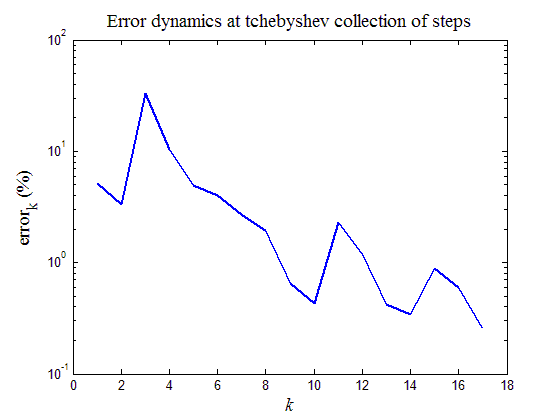
Рис.5. Динамика ошибки решения, полученная методом установления (34), в зависимости от номера шага
После отработки кода программы листинга_№5 получится график, приведенный на рис.5. Итоговый график представляет динамику ошибки (42) в схеме на установление (34) в зависимости от номера шага с чебышевским набором шагов в последовательности (38). Из графика видно как ошибка совершает колебания, возникающие при чередовании шагов превышающих и не достигающих порога устойчивости. В целом же видно, что точность расчета существенно повышается к концу последнего шага и становится меньше заданной точности в 1%.