Листинг_№2

%Программа построения трехмерного профиля

%множителя роста гармоник при переходе со

%слоя на слой в продольно-поперечной схеме и

%графика зависимости сомножителя gamma от q

clear all

a=1; b=1;%габариты прямоугольной области

N=100; M=100;%число узлов сетки по x1 и x2

h1=a/N; h2=b/M;%шаги равномерной сетки по x1 и x2

%Оптимальное значение шага по времени

tau=(a*b)/(pi*sqrt(N*M));

%Цикл построения трехмерного профиля множителя

%роста гармоник

for q=1:(N-1)

alpha=((2*tau)/h1^2)*sin((pi*q*h1)/(2*a))^2;

for r=1:(M-1)

beta=((2*tau)/h2^2)*sin((pi*r*h2)/(2*b))^2;

ro(q,r)=((1-alpha)*(1-beta))/...

((1+alpha)*(1+beta));

end

end

%Рисуем трехмерный профиль множителя роста

n1=1:(N-1); n2=1:(M-1);

subplot(1,2,1); surf(n2,n1,ro);

%Определяем зависимость gamma от q

for q=1:(N-1)

alpha=((2*tau)/h1^2)*sin((pi*q*h1)/(2*a))^2;

gamma(q)=(1-alpha)/(1+alpha);

end

%Рисуем график зависимости gamma от q

subplot(1,2,2); plot(n1,gamma);

Оценку величины оптимального шага в (23) следует рассматривать как довольно грубую. Например, в книге¹ величина оптимального шага оценивалась, исходя из уравнения , согласно которому

. (23)

Оценки величины оптимального шага (23), (23) протестируем на примере решения двумерного эволюционного уравнения (16) с помощью продольно-поперечной разностной схемы. На листинге_№3 приведен соответствующий программный код.

Листинг_№3

%Программа численного определения величины

%оптимального шага по времени в процессе

%решения двухмерного уравнения теплопроводности

%(11) с помощью продольно-поперечной схемы

function optimum

global a b vc0 r0 r1

%Определяем габариты области интегрирования

%по времени, направлениям x1 и x2, а также

%константу vc0, задающую амплитуду

%начального распределения

a=1; b=1; vc0=100;

r0=0.2*min(a,b); r1=0.4*min(a,b);

%Задаем точность расчета на установление eps

eps=1e-8;

%Определяем число шагов по направлениям x1 и x2

N=41; M=41; h1=a/(N-1); h2=b/(M-1);

%Определяем сетки по x1 и x2

x1=0:h1:a; x2=0:h2:b;

%Оцеваем оптимальный шаг по формуле (23)

tau0=(a*b)/(pi*sqrt(N*M));

%Оцениваем оптимальный шаг по формуле (23')

tau1=(1/pi)*(a^2/N^2+b^2/M^2)^0.5*(1/a^2+1/b^2)^(-0.5);

%Выводим численные оценки величины оптимального шага

[tau0 tau1]

%Формируем массив шагов по времени

tau=(tau0/10):(tau0/10):(4*tau0);

k=0;

%Формируем цикл расчетов с различными шагами по времени

for tu=1:length(tau)

%Определяем начальные данные в виде кольца

for n=1:N

for m=1:M

y1(n,m)=v0(x1(n),x2(m));

end

end

%Организуем основной цикл интегрирования по времени

nrm=max(max(abs(y1)));

step(tu)=0;

%Формируем цикл по времени решения уравнения (16)

%на установление, т.е. до тех пор, пока не будет

%достигнута нужная точность eps

while (nrm>eps)&(step(tu)<300)

p1=(0.5*tau(tu))/h1^2;

p2=(0.5*tau(tu))/h2^2;

%Находим решение на полуцелом временном слое,

%т.е. решаем уравнение (11.39)

for m=2:(M-1)

%Учитываем нулевое граничное при x1=0

alpha(2)=0; beta(2)=0;

for n=2:(N-1)

alpha(n+1)=p1/(1+p1*(2-alpha(n)));

beta(n+1)=(y1(n,m)+p2*(y1(n,m-1)-...

2*y1(n,m)+y1(n,m+1))+p1*beta(n))/...

(1+p1*(2-alpha(n)));

end

%Учитываем нулевое граничное при x1=a

ys(N,m)=0;

for n=N:-1:2

ys(n-1,m)=alpha(n)*ys(n,m)+beta(n);

end

end

%Находим решение на следующем временном слое,

%т.е. решаем уравнение (11.39')

for n=2:(N-1)

%Учитываем нулевое граничное при x2=0

alpha(2)=0; beta(2)=0;

for m=2:(M-1)

alpha(m+1)=p2/(1+p2*(2-alpha(m)));

beta(m+1)=(ys(n,m)+p1*(ys(n-1,m)-...

2*ys(n,m)+ys(n+1,m))+p2*beta(m))/...

(1+p2*(2-alpha(m)));

end

%Учитываем нулевое граничное при x2=b

y2(n,M)=0;

for m=M:-1:2

y2(n,m-1)=alpha(m)*y2(n,m)+beta(m);

end

end

for m=1:M

y2(1,m)=0; y2(N,m)=0;

end

%Находим норму решения эволюционной задачи в L2

s=0;

for n=1:N

for m=1:M

s=s+h1*h2*y2(n,m)^2;

end

end

nrm=sqrt(s);

y1=y2;

step(tu)=step(tu)+1;

end

end

%Рисуем график зависимости числа шагов в задаче на

%установление с заданной точностью eps от шага

%интегрирования по времени

plot(tau,step);

%Определяем функцию начального распределения

function y=v0(x1,x2)

global a b vc0 r0 r1

r=sqrt((x1-0.5*a)^2+(x2-0.5*b)^2);

y=0;

if (r>=r0)&(r<=r1)

y=vc0*(r1-r)*(r-r0);

end

Работа программы листинга_№3 генерирует вывод двух чисел в командное окно MATLAB и графика, примерный вид которого приведен на рис.3. Пара чисел соответствует оценкам оптимального шага по двум формулам (23) и (23). Эти оценки довольно близки, отличия проявляются, когда N и M заметно отличаются. На рис.3 виден отчетливый минимум при выборе величины шага интегрирования по времени с помощью продольно-поперечной схемы. При данном конкретном значении параметров теоретические оценки оптимального шага по формулам (23) и (23) довольно близки к истинному значению, полученному из графика рис.3.

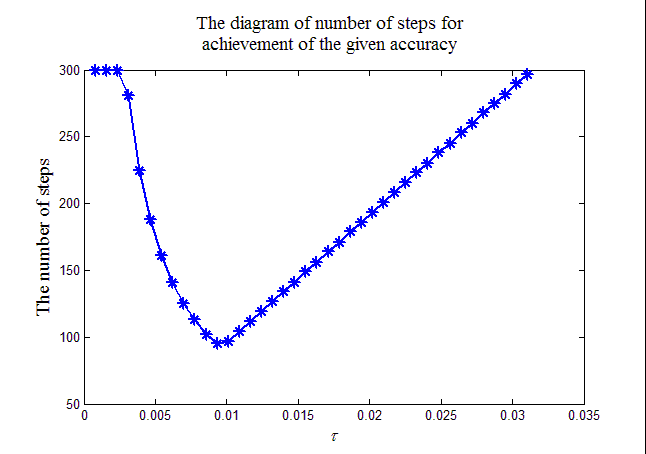
Рис.3. График зависимости числа шагов в продольно-поперечной схеме для достижения заданной точности от шага сетки по времени

Минимальное число шагов K необходимое для достижения заданной точности  определяется из условия . Для оценки числа K выберем в качестве шага по времени — оптимальный шаг (23), а также предположим, что a = b и N = M, тогда нетрудно подсчитать согласно (20) — (21), что , т.е.

или ,

где T — время счета на установление (14). Таким образом, минимально необходимое число шагов по времени для достижения заданной точности реализуемое при оптимальном шаге (23) пропорционально числу узлов сетки по пространству.

Локально-одномерная схема (11.48), (11.49) с полусуммой по времени в двумерном случае допускает аналогичные выводы о наличии оптимального шага по времени для достижения заданной точности в счете на установление.

Действительно, представим локально-одномерную схему в виде:

, (24)

, (24)

где операторы ₁, ₂ определены в (17) и коммутируют друг с другом. Умножим уравнение (24) слева на E + ½ ₂, а уравнение (24) — на E — ½ ₁, тогда, после исключения , найдем

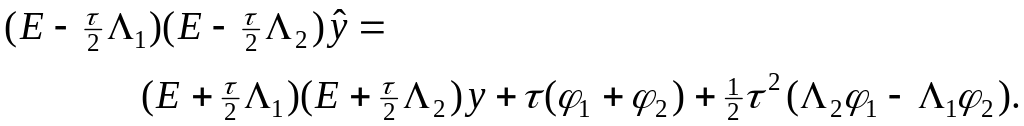
Последнее уравнение может быть преобразовано к канонической форме (17), т.е.

, (25)

где операторы A и B определены в (17). Поскольку левая часть локально-одномерной схемы (25) совпадает с левой частью продольно-поперечной схемы (17), постольку минимальное количество шагов для достижения заданной точности в схеме на установление реализуется при некотором оптимальном шаге ₀, оценка которого приведена в формулах (23), (23).

В общем случае, когда размерность два и более, область по пространству сложно устроена и пр., заранее неизвестно, какое число шагов необходимо совершить до установления. Поэтому на практике используют тот или иной нестрогий критерий установления. Без обсуждения приведем следующие три критерия сходимости:

,

,

.

Чебышевский набор шагов. Счет на установление может быть проведен с переменным шагом по времени. В задачах, в которых границы спектра разностных операторов известны, построены специальные наборы шагов _k, k = 1,…K, обеспечивающие более быстрое затухание начальных данных, чем в случае расчетов с одним-единственным оптимальным шагом.

Пусть разностная схема может быть приведена к канонической двухслойной форме:

, (26)

где, как обычно считается, что A и B — самосопряженные положительно определенные операторы, удовлетворяющие неравенствам

. (27)

Затухание начальных данных определяется однородным уравнением (26) при  = 0. Обозначая решение однородного уравнения (26) символом z^(k), k = 1,…,K, перепишем его в форме

, (28)

где

. (28)

Согласно (28), имеем

. (29)

Из (29) видно, что для наиболее быстрого затухания начальных данных последовательность шагов _k, k = 1,…K надо подобрать так, чтобы была минимальна при заданном числе шагов K.

Поскольку A и B — самосопряженные операторы, оператор C также самосопряженный, причем согласно (27) следует следующая оценка:

. (30)

С учетом (30) норму операторного многочлена можно оценить по формуле

,

где — алгебраический многочлен. Известно, что многочлен, минимально уклоняющийся на отрезке от нуля, является многочленом Чебышева². Учитывая это обстоятельство, можно использовать следующий чебышевский набор шагов:

. (31)

Считая многочлен многочленом Чебышева, можно оценить его максимальное отклонение от нуля согласно формуле:

. (32)

Отбросим в (32), считая что это слагаемое много меньше единицы, тогда число шагов K в схеме счета на установление (26) с чебышевским набором шагов по времени для достижения заданной точности , можно представить в виде следующей формулы:

(33)

Проиллюстрируем использование чебышевского набора шагов по времени на примере счета на установление с помощью явной разностной схемы вида

. (34)

Схема (34) записана в канонической форме (26), поскольку B = E и A =  (₁ + ₂). Найдем ₁, ₂, которые, согласно (27), определяют пределы изменчивости оператора A, т.е. . Для этого достаточно найти минимальное и максимальное собственные значения оператора A =  (₁ + ₂). Задача на собственные значения оператора A решена в учебнике³, где приведено следующее выражение для собственных значений

. (35)

Учитывая, что q = 1,…,N1 r = 1,…,M1 в (35), найдем

. (36)

Учитывая, что и , оценим по порядку величины число K в расчете на установление с чебышевским набором шагов. Для этого положим, что a = b, N = M >>1, тогда , , . Подставляя значение  в (33), находим искомое число шагов для достижения заданной точности :

. (37)

Оценка (37) говорит о том, что данная процедура эквивалентна экономичным схемам с постоянным оптимальным шагом.

Явная схема (34) устойчива только при условии, что . Среди чебышевского набора шагов (31) есть как большие , так и меньшие . Большие шаги вызывают рост погрешности, меньшие — ее затухание. В целом же после K шагов ошибка уменьшится в . Ошибки на промежуточных шагах могут возрасти настолько сильно, что превысят пределы памяти, отводимые для чисел с плавающей запятой (в MATLAB под тип double отводится 64 бит или 8 байт) и расчет не удастся довести до конца. Для преодоления этой трудности необходимо выбирать шаги Чебышева в таком порядке, чтобы отдельный локальный рост в начальных данных был скомпенсирован соответствующим затуханием при последующих шагах. На листинге_№4 приведена небольшая программа, которая изображает последовательность чебышевских шагов (31) для разностной схемы (34) при некотором выборе параметров.