Плохотников К.Э. ВЫЧИСЛИТЕЛЬНЫЕ МЕТОДЫ. Теория и практика в среде MATLAB

Лекция №12 Эллиптические уравнения Счет на установление

Эллиптические уравнения как стационарные решения эволюционных задач. К эллиптическим уравнениям приводит множество физических задач. К ним относятся: определение прогиба нагруженной мембраны, балки и прочие задачи из теории сопротивления материалов, оценка стационарного, т.е. независимого от времени распределения тепла в теле, стационарные течения жидкости, газа в трубах и т.д. Все множество такого рода задач имеет общее свойство, согласно которому считается, что внешние воздействия не зависят от времени, а начальные данные заданы были столь давно, что физическая система успела забыть об этом воздействии и решение стало стационарным и не зависящим от времени, т.е. u = u(r), r = (x₁,…,x_p).

Примером эллиптического уравнения является задача Дирихле с краевыми условиями первого рода, согласно которой требуется найти непрерывное решение задачи

u(r) =  f(r), r  G, u_(r) = (r), (1)

где , G = G(r) — многомерная замкнутая область с границей . В отличие от эволюционных уравнений, задача (1) начальные данные не содержит. Обобщением задачи (1) в контексте, например, стационарного уравнения теплопроводности из предыдущей лекции, является уравнение вида:

div[k(r)gradu(r)] =  f(r), r  G, u_(r) = (r), (2)

где k(r) > 0— коэффициент теплопроводности.

Задачу (2) принято называть стационарной на фоне эволюционного уравнения параболического типа с теми же граничными условиями и с произвольными начальными данными:

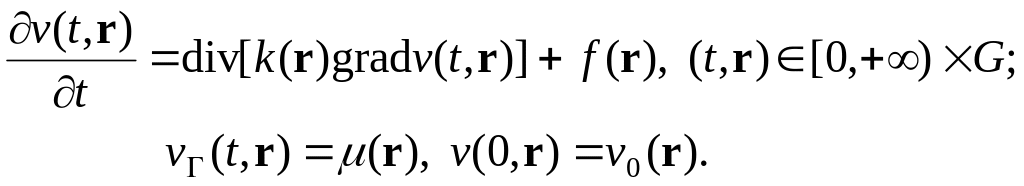(3)

Исследуем вопрос об отличие решения эволюционной задача v(t,r) от решения стационарной задачи u(r). Для этого вычтем уравнение (2) из уравнения (3) и введем обозначение w(t,r) = v(t,r)  u(r), тогда

(4)

Эволюционная задача (4) имеет однородные (нулевые) краевые условия и произвольные начальные данные, т.к. функция v₀(r) считалась произвольным начальным распределением.

В курсе математической физики^ показано, что решение задачи (4) с помощью метода разделения переменных можно представить в виде следующего бесконечного ряда:

, (5)

где _q, w_q(r) — собственные значения и собственные функции многомерной задачи Штурма-Лиувилля:

. (6)

С учетом (6) коэффициенты c_q, входящие в (5), можно назвать коэффициентами Фурье начальных данных задачи (4) по системе собственных функций w_q(r), т.е.

.

Собственные значения _q задачи (6) положительны и образуют неубывающую последовательность

, (7)

а собственные функции w_q(r) образуют полную ортонормированную систему в G(r).

Согласно (5), (7), можно получить следующую оценку для нормы решения w(t,r) уравнения (4):

. (8)

Неравенство (8) означает, что разность экспоненциально в норме при t  . Другими словами, решение v(t,r) эволюционной задачи (3) среднеквадратично сходится к решению u(r) стационарной задачи (2) при t  .

Из изложенного выше следует, что вместо задачи (2) для эллиптического уравнения можно взять эволюционную задачу (3) для параболического уравнения с аналогичным пространственным оператором, произвольно выбрать начальные данные и вычислить решение v(t,r) при достаточно большом значении времени t. Стационарный предел u(r), к которому стремится v(t,r) при t   является решением стационарной задачи (2).

Такой способ решения эллиптического уравнения называется счетом на установление. Этот способ позволяет использовать для решения эллиптических задач хорошо апробированные схемы решения параболических уравнений, например, продольно-поперечную схему для двумерной задачи и локально-одномерную — для многомерных задач.

Поскольку сходимость к стационарному решению экспоненциальная, т.е. довольно быстрая, постольку, задавая точность , можно дать следующую оценку для момента достижения нужной точности в счете на установление:

, (9)

где ₁ — наименьшее собственное значение соответствующей задачи Штурма-Лиувилля (6).

Протестируем процедуру счета на установление на примере численного решения двумерного эллиптического уравнения с однородными граничными условиями в прямоугольной области. Запишем соответствующую задачу в следующем виде:

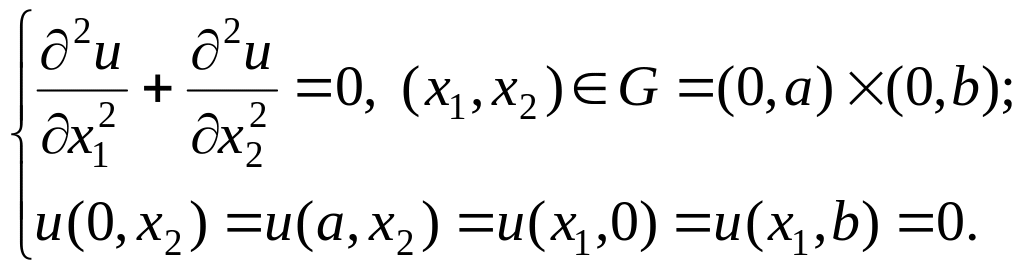(10)

Задача (10) имеет очевидное решение u(x₁,x₂) = 0. Построим соответствующую эволюционную задачу:

(11)

добавим к ней произвольные начальные данные:

v(0,x₁,x₂) = v₀(x₁,x₂). (12)

Методом разделения переменных легко решить соответствующую уравнению (11) задачу Штурма-Лиувилля. Получаются следующие собственные значения и собственные функции:

, (13)

где q, r = 1,2,… Из (13) легко найти минимальное собственное значение: , которое позволяет оценить время счета на установление

(14)

с заданной точностью .

Задачу (11) решим численно с помощью продольно-поперечной схемы (11.39), (11.39) на временном отрезке [0,T]. Зададимся для определенности точностью  = 10^8 и рассмотрим соответствующий код программы, представленный на листинге_№1.