Листинг_№10

%Программа сравнения разностных схем (40), (45)

%на примере динамики образования ударной волны

%Очищаем рабочее пространство

clear all

%Задаем пределы области интегрирования G=[0,T]x[0,a]

T=4; a=2;

%Задаем параметры сетки по времени и пространству

tau=0.001; h=0.01; r=tau/h;

%Определяем параметры псевдовязкости схем (40), (45)

nu=1; nu1=0.1;

%Задаем сетки по времени и пространству

t=0:tau:T; x=0:h:a;

Nt=length(t); Nx=length(x);

%Определяем левое граничное условие u(t,0)=0

for m=1:Nt

y(m,1)=0;

end

%Определяем правое граничное условие u(t,0)=0

for m=1:Nt

y(m,Nx)=0;

end

%Определяем начальное условие u(0,x)=sin(pi x)^2,

%0<=x<=1; u(0,x)=0, 1<x<=2

for n=1:Nx

if x(n)<=1

y(1,n)=sin(pi*x(n))^2;

else

y(1,n)=0;

end

end

%Организуем цикл расчета по схеме (40) на различные

%моменты времени

for m=1:(Nt-1)

for n=2:(Nx-1)

y(m+1,n)=(1-r*(y(m,n)-y(m,n-1)))*y(m,n)-...

0.5*r*nu^2*(y(m,n+1)-y(m,n-1))*...

(y(m,n+1)-2*y(m,n)+y(m,n-1));

end

end

%Рисуем профили волны в различные моменты времени на

%одном и том же графике в координатах решение -

%пространственная координата

for m=1:35:Nt

subplot(1,2,1);

plot(x,y(m,:));

hold on

end

%Организуем цикл расчета по схеме (45) на различные

%моменты времени

for m=1:(Nt-1)

for n=2:(Nx-1)

y(m+1,n)=(1-r*(y(m,n)-y(m,n-1)))*y(m,n)+...

r*nu1*(y(m,n+1)-2*y(m,n)+y(m,n-1));

end

end

%Рисуем профили волны в различные моменты времени

for m=1:35:Nt

subplot(1,2,2);

plot(x,y(m,:));

hold on

end

Итоговый результат работы кода листинга_№10 представлен на рис.14. Слева на рис.14 приведены профили волны на различные моменты времени, рассчитанные по разностной схеме (40). Жирными линиями на графике выделено начальное распределение и уже сформировавшаяся ударная волна в последний момент времени. Заметно, что ударная волна слегка размазана в соответствии с выбором величины параметра . Аналогичная картина представлена на рис.14 справа, где приведены результаты расчета по “линейной” разностной схеме (45). Визуальное сравнение левого и правого рисунков показывает их неплохое совпадение. Это удалось добиться за счет подбора параметра ₁.

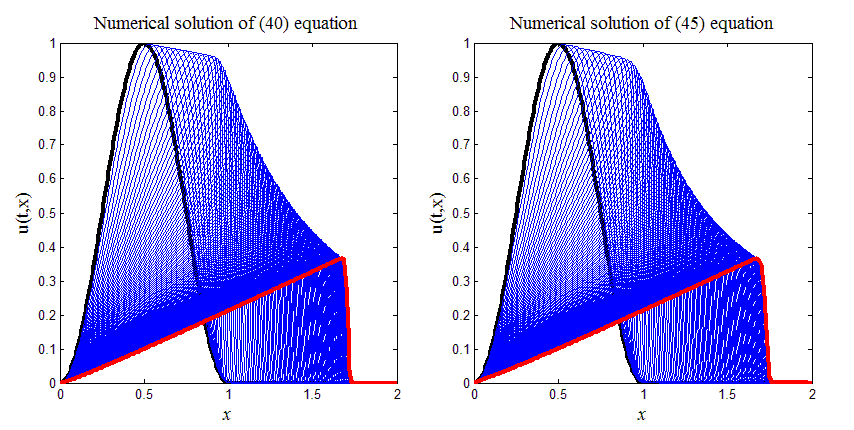
Рис.14. Изучение механизма образования ударной волны на примере решения квазилинейного уравнения переноса с помощью разностных схем (40), (45)

Консервативные схемы. В условиях высокой степени неопределенности процедуры составления разностных схем, одним из важнейших свойств, которым может удовлетворять схема является свойство консервативности — следствие того или иного закона сохранения.

Рассмотрим закон сохранения на примере уравнения переноса, записанного в дивергентной форме (33). Выберем некоторую ячейку сетки и проинтегрируем по ней уравнение (33), тогда получится следующее точное интегральное соотношение:

. (46)

Уравнение (33) можно проинтегрировать по всей области G(t,x) = [x₀,x_N][t₀,t_M] и получить выражение, аналогичное (46), т.е.

. (47)

Уравнение (47) напоминает физический закон сохранения, где первый интеграл описывает изменение величины за истекшее время, а второй интеграл есть разность потоков через правую и левую границы области G. Выражение (47) является законом сохранения для квазилинейного уравнения переноса (28). Аналогично можно рассматривать уравнение (46) в качестве закона сохранения, но для отдельной ячейки, где также есть сохраняемая величина и потоки на соответствующих границах. Просуммируем теперь уравнение (46) по всем ячейкам области G, тогда

. (48)

Совершенно очевидно, что интегралы по внутренним границам области G взаимно уничтожаются и остаются интегралы только по наружным границам, т.е. приходим к закону сохранения в форме (47). Таким образом, закон сохранения во всей области есть следствие закона сохранения в отдельных ячейках.

Не всякая разностная схема обладает таким свойством. Схемы, в которых закон сохранения во всей области является следствием закона сохранения в отдельных ячейках, называются консервативными. Если в некоторой схеме разностный закон сохранения нарушается во всей области G, то такую схему называют неконсервативной.

Построим некоторые примеры консервативных схем. Аппроксимируем интегралы в (47) по формулам прямоугольника^, тогда получим явную схему следующего вида:

. (49)

Консервативность разностной схемы (49) проверяется непосредственно суммированием по m и n, т.е.

. (50)

Выражение (50) является конечно-разностной аппроксимацией закона сохранения в форме (47).

Можно построить и другие консервативные разностные схемы, выбирая различные шаблоны. Например, следуя шаблону рис.2,в, можно получить консервативную неявную схему бегущего счета:

. (51)

Решая квадратное уравнение (51) относительно и выбирая положительное значение корня, находим

. (51)

Построены также схемы, которые удовлетворяют многим законам сохранения. Такие схемы называют полностью консервативными.

Изучим схемы (49), (51) на предмет описания процесса образования ударной волны. На листинге_№11 приведен код соответствующей программы.