Листинг_№9

%Программа рисования по формуле (38)

%последовательности формирования

%ударной волны при eps -> 0

%очищаем рабочее пространство

clear all

%задаем параметры функции (38)

a=2; b=0.2; eps=2;

%определяем переменную xi=x-Vt

xi=-2:0.01:2;

%Формируем цикл построения графиков

%ueps при различных значениях eps

for i=1:10

%уменьшаем текущее значение

%значение eps вдвое

eps=eps/2;

for j=1:length(xi)

if xi(j)<-0.5*pi*eps

ueps(j)=a;

end

if (xi(j)>=(-0.5*pi*eps))&...

(xi(j)<=(0.5*pi*eps))

ueps(j)=0.5*(a+b)-...

0.5*(a-b)*sin(xi(j)/eps);

end

if xi(j)>0.5*pi*eps

ueps(j)=b;

end

end

axis([-2 2 0 2]);

plot(xi,ueps,'LineWidth',2);

hold on

end

Обычно коэффициент псевдовязкости связывается с шагом сетки по пространству, т.е. считают, что

 =  h,  = const, (39)

тогда любой сильный разрыв согласно (38) размазывается на одно и то же число шагов сетки  / h = . В этом случае при h  0 уравнение с псевдовязкостью переходит в исходное квазилинейное уравнение (28), а размазанная ударная волна (38) переходит в разрывную ударную волну.

Составим для уравнения с псевдовязкостью (35) явную разностную схему на равномерной сетке:

(40)

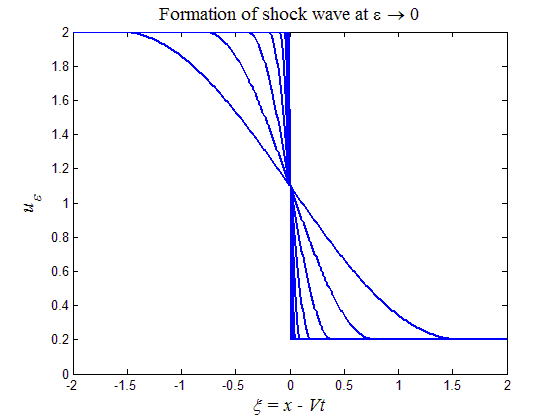
Рис.13. Образование разрывного решения — ударной волны при   0 согласно представлению (38)

Исследуем вопрос об устойчивости разностной схемы (40). Поскольку разностная схема (40) является нелинейной, линеаризуем ее, определяя уравнение для погрешности y:

(41)

Поскольку коэффициенты при y являются переменными, для дальнейшего исследования вопроса устойчивости схемы (40) воспользуемся принципом “замороженных” коэффициентов. Согласно этому принципу коэффициенты при y считаются постоянными величинами. Проведем в (41) замены и т.д., тогда

(42)

Изучим рост ошибки, которая имеет вид . Подставим в (42) выражения

,

тогда множитель роста гармоники предстанет в виде:

. (43)

Если коэффициент псевдовязкости выбран согласно (39), то величина в квадратных скобках в (43) равномерно ограничена по шагу h. В этом случае последний член в (43) имеет порядок O() и не влияет на устойчивость разностной схемы (40). Первые два члена в правой части уравнения (43) для обеспечения условия устойчивости разностной схемы (40) приводят к условию, аналогичному условию Куранта:

.

Схема (40) является примером так называемой однородной разностной схемы для решения задач с произвольным числом движущихся разрывов, число которых может меняться со временем. Отметим, что помимо псевдовязкости уравнения (35), применяют также псевдовязкость, именуемую линейной. Она имеет следующий вид:

, (44)

где , ₁ = const. Уравнение (44) напоминает уравнение теплопроводности все решения которого достаточно гладкие.

Для уравнения (44) определим явную разностную схему вида:

. (45)

Проведем сравнительный численный анализ схем (40) и (45). На листинге_№10 приведен код соответствующей программы расчета образования ударной волны по схемам (40) и (45).