Листинг_№8

%Программа рисования приближенных

%характеристик (30)

%очищаем рабочее пространство

clear all

%задаем размеры области G=[0,T]x[0,a] и

%константу alpha

T=1; a=1; alpha=0.3;

%определяем набор значений констант t0 и x0

t0=0:0.1:T; x0=0:0.1:a;

t=0:0.1:T; x=0:0.1:a;

%рисуем характеристики, выходящие из

%левого граничного условия

for m=1:length(t0)

for n=1:length(x)

y(n)=(exp(alpha*x(n))-1)/alpha+...

t0(m)*exp(alpha*x(n));

end

plot(x,y);

hold on

end

%рисуем характеристики, выходящие из

%начального условия

for n=1:(length(x0)-1)

x=x0(n):((a-x0(n))/10):a;

for nn=1:length(x)

y(nn)=log((1+alpha*x(nn))/...

(1+alpha*x0(n)))/alpha;

end

plot(x,y);

hold on

end

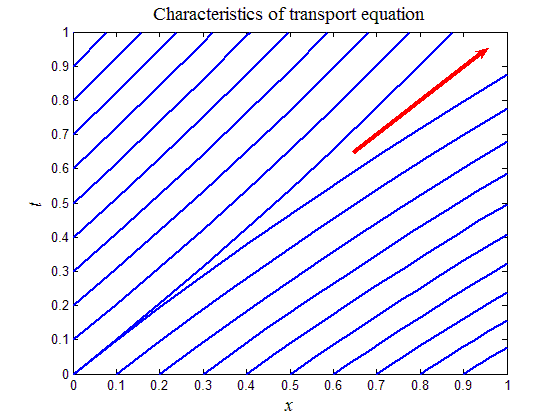
Рис.11,а. Характеристики первого типа начальных данных	Рис.11,б. Характеристики второго типа начальных данных с пустой областью	Рис.11,в. Характеристики второго типа начальных данных с доопределенной пустой областью

Второй тип начальных данных. Краевое и начальное значения монотонны как в первом случае, но имеют разрывы. Для упрощения ситуации положим

(31)

На рис.11,б приведены соответствующие характеристики. В силу (31) характеристики приближенно можно представить прямыми линиями, которые имеют одинаковый наклон левее и правее точки разрыва x₀. Из точки разрыва начальных данных x₀ выходит две характеристики, выделенные на рис.11,б жирными стрелками красного цвета. Между этими линиями нет ни одной характеристики и решение в этой области не определено.

Потребуем, чтобы задача была корректной, т.е. устойчивой относительно бесконечно малых возмущений начальных данных. Для этого заменим разрыв в начальных данных на монотонный переход в бесконечно узком интервале. Тогда пустая область на рис.11,б будет заполнена набором характеристик, аналитический вид которых следующий:

(32)

На рис.11,в приведен вид характеристик (две черные стрелки) в пустой области разрыва начальных данных. В итоге доопределения с помощью (32) решение непрерывно на всей плоскости, кроме точки (0,x₀). Таким образом, разрыв начальных данных сглаживается со временем, но след разрыва остается. Этот след в виде разрыва производных передается по двум характеристикам, выходящим из точки разрыва x₀. Во всех остальных точках решение будет гладким, если соответствующие граничные и начальные данные были гладкими.

Разрыв производных называют слабым разрывом решения. Слабые разрывы квазилинейного уравнения переносятся по характеристикам.

Третий тип начальных данных. Пусть нарушено условие монотонности, предполагаемое в двух предыдущих случаях. Положим, как и в (31),

но теперь a > b > 0. В этом случае характеристики будут иметь вид, представленный на рис.12,а.

В угле, образованном жирными (красными) стрелками, через каждую точку проходит две характеристики, каждая из которых приносит свое значение начальных данных, т.е. вне этого угла решение однозначно определено, а внутри угла решение однозначно не определено. В этом случае непрерывное решение построить не удается, т.е. решение должно быть разрывным или обобщенным решением дифференциального уравнения (28).

Обобщенное решение удовлетворяет некоторому интегральному уравнению, которое получается из специальной дивергентной формы записи дифференциального уравнения. Разные дивергентные формы записи одного и того же уравнения приводят к разным разрывным решениям, при этом гладкие решения для всех дивергентных форм одинаковы. Дивергентная форма, представляющая физический закон сохранения, определяет правильное решение, которое еще называют допустимым.

Рис.12,а. Характеристики третьего типа начальных данных	Рис.12,б. Построение обобщенного, разрывного решения	Рис.12,в. Обобщенное, разрывное решение и поле характеристик

Квазилинейное уравнение переноса (28) легко переписать в одной из дивергентных форм:

. (33)

Нас интересует решение, имеющее единственный разрыв. Пусть наклон линии разрыва соответствует скорости V, и разрыв двигается как волна. Из вида характеристик на рис.12,а следует, что искомое разрывное решение должно иметь следующий вид:

Проинтегрируем дивергентную форму (33) по площади прямоугольника со сторонами  и h = V, и левый нижний угол которого находится в точке разрыва x₀ (рис.12,б), тогда

откуда находим скорость распространения разрыва

. (34)

Разрыв решения называют сильным разрывом, а в газовой динамике такой разрыв называют ударной волной. Сильный разрыв квазилинейного уравнения переноса распространяется не по характеристике. Так, на рис.12,б жирная стрелка, по которой распространяется разрыв, не является характеристикой. В теории квазилинейных уравнений доказывается, что только обобщенное решение устойчиво относительно малых возмущений начальных данных.

Четвертый тип начальных данных. В этом случае функция начального условия u(0,x) непрерывна и убывает на некотором интервале, что переадресует нас к третьему типу. Пересечение характеристик также приводит к образованию сильного разрыва (рис.12,в), скорость которого описывается уравнением, подобным (34). Однако в этом случае скорость сильного разрыва может меняться.

Псевдовязкость. Основную трудность при расчетах по разностным схемам доставляют сильные разрывы решения. Прием по преодолению этой трудности состоит в том, чтобы внести в исходное уравнение такую “малую” добавку, чтобы исходные разрывные решения стали непрерывными и достаточно гладкими. Составляя для нового уравнения соответствующую разностную схему, можно получить нужное решение.

Гладкие решения характерны для уравнений с диссипативными членами типа диффузии, теплопроводности или вязкого трения. Добавляемый в исходное уравнение член, оказывающий выглаживающее воздействие, принято называть псевдовязкостью или искусственной, математической вязкостью.

Рассмотрим пример. Добавим в исходное квазилинейное уравнение (28) соответствующий член, тогда

, (35)

где третье слагаемое выступает в качестве псевдовязкости, а коэффициент  ² считается малым.

Видно, что для гладких, дважды непрерывно-дифференцируемых функций решения уравнения (28) близки к решениям уравнения (35).

Поищем среди гладких решений уравнения (35) решение, напоминающее ударную волну:

где b < a и скорость ударной волны . Рассмотрим автомодельное решение в виде бегущей волны

. (36)

После подстановки (36) в (35), находим

. (37)

Приравнивая каждый из сомножителей в (37) к нулю, получаем два решения:

из которых можно сконструировать решение, похожее на слегка размытую с шириной ~ ударную волну:

(38)

Решение (38) непрерывно-дифференцируемо и при   0 сходится к разрывному решению — ударной волне. На листинге_№9 приведен код программы рисования последовательности профилей (38), приводящих к образованию ударной волны при   0. Итоговый рисунок приведен на рис.13.