Листинг_№6

%Программа рисования характеристик

%t=sqrt(A-ln(xv-x)^2) уравнения

%du/dt+t(xv-x)du/dx=0

%очищаем рабочее пространство

clear all

%задаем размеры области G=[0,T]x[0,a]

T=1; a=1;

%определяем координату xv, на которой

%скорость переноса меняет знак

xv=0.5;

t=0:0.1:T;

%Определяем значения константы A

for m=1:length(t)

A(m)=t(m)^2+log(xv^2);

end

%Рисуем характеристики, выходящие из

%левой границы области G=[0,T]x[0,a]

x=0:0.001:(xv-1e-4);

for m=1:length(A)

for n=1:length(x)

y(n)=sqrt(A(m)-log((xv-x(n))^2));

end

plot(x,y);

hold on

end

%Рисуем характеристики, выходящие из

%правой границы области G=[0,T]x[0,a]

x=(xv-1e-4):0.001:a;

for m=1:length(A)

for n=1:length(x)

y(n)=sqrt(A(m)-log((xv-x(n))^2));

end

plot(x,y);

hold on

end

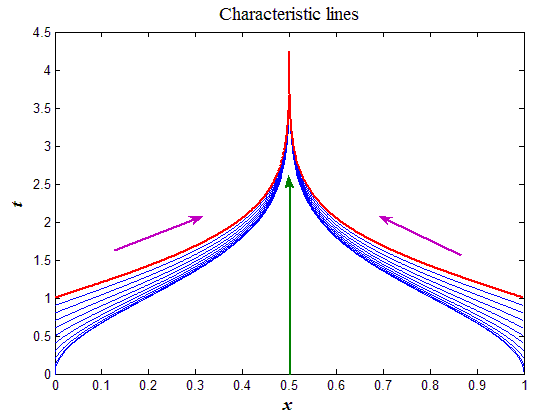
Рис.9,а. Характеристики (23) уравнения (21)	Рис.9,б. Шаблон разностной схемы для уравнения (24)

Возвращаясь к вопросу о корректности уравнения переноса со скоростью переноса меняющей знак и учитывая пример (21) — (23), можно констатировать, что необходимо задавать два граничных условия на левой и правой границах области G(t,x) = [0,T][0,a], т.е.

(24)

Согласно (24), каждая из двух границ области (левая и правая) имеют свою зону влияния, которые разделены линией (вертикальная стрелка на рис.9,а). В каждой зоне можно использовать свою схему бегущего счета с учетом направления расчета.

Есть и другой способ. Построим для шаблона рис.9,б неявную разностную схему:

(25)

С учетом направления характеристик (стрелки на рис.9,а) и принимая во внимание шаблон на рис.9,б видно, что при любом знаке скорости c и при любом соотношении шагов по времени  и пространству h значение вычисляется интерполяцией. Методом разделения переменных можно убедиться, что схема устойчива при любом знаке c.

Поскольку разностная схема на следующем слое связывает три соседних узла, постольку для решения полученной системы уравнений необходимо привлекать метод прогонки. Теоретические основы метода прогонки обсуждались в лекции №5. Применяя достаточное условие устойчивости метода прогонки (условие диагонального преобладания), приходим к условию Куранта в форме:

. (26)

Условие Куранта (26) для применимости метода прогонки является достаточным, поэтому при его нарушении схема (25) может все еще давать разумные численные решения. Исследуем этот вопрос на примере решения дачи (24) в виде:

(27)

Задача (27) имеет аналитическое решение

.

На листинге_№7 приведен код программы численного решения задачи (27) с помощью разностной схемы (25) для сеток разной длины по времени и пространству.

Листинг_№7

%Программа численного решения задачи (27)

%Очищаем рабочее пространство

clear all

%Определяем область интегрирования G=[0,T]x[0,a] и

%прямую x=xv, на которой скорость в уравнении

%переноса меняет знак

T=1; a=1; xv=0.5;

k=1;

%Организуем цикл решения задачи (27) для различных

%сеток: Nt - число узлов в сетке по времени,

%Nx - число узлов в сетке по пространству

for Nt=10:10:100

for Nx=10:10:100

%вычисляем шаг по времени и по пространству

tau=T/(Nt-1); h=a/(Nx-1);

%определяем начальное условие

for n=1:Nx

y(1,n)=-log((xv-h*(n-1))^2);

end

%программируем процедуру прогонки решения

%задачи (27) по разностной схеме (25)

for m=1:(Nt-1)

alpha(2)=0;

beta(2)=-(tau*m)^2-log(xv^2);

for n=2:(Nx-1)

c=tau*m*(xv-h*(n-1));

r=(tau*c)/(2*h);

alpha(n+1)=-r/(1-r*alpha(n));

beta(n+1)=(y(m,n)+r*beta(n))/...

(1-r*alpha(n));

end

y(m+1,Nx)=-(tau*m)^2-log((xv-a)^2);

for n=Nx:-1:2

y(m+1,n-1)=alpha(n)*y(m+1,n)+beta(n);

end

end

%оцениваем ошибку численного решения, как

%разность численного решения и аналитического

%решения в норме l2

s=0;

for m=2:(Nt-1)

for n=2:(Nx-1)

s=(y(m,n)+(tau*(m-1))^2+...

log((xv-h*(n-1))^2))^2*tau*h;

end

end

%запоминаем норму ошибки и число узлов NtNx

%разностной схемы в области интегрирования G

error_l2(k)=sqrt(s);

gr(k)=Nt*Nx;

k=k+1;

end

end

t=0:tau:T;

x=0:h:a;

%Рисуем численное решение задачи (27) в области G

%с максимальным количеством узлов NtNx

subplot(1,2,1); surf(x,t,y);

%Рисуем график зависимости ошибки численного

%решения задачи (27) в норме l2 от произведения NtNx

subplot(1,2,2); plot(gr,error_l2);

На рис.10 приведен итог работы кода программы листинга_№7. На рис.10 слева изображено численное решение задачи (27) согласно разностной схеме (25) при выборе области интегрирования G(t,x) = [0,1][0,1]. По времени и пространству выбирались равномерные сетки: 0 = t₁ < … < t₁₀₀ = 1 и 0 = x₁ < … < x₁₀₀ = 1. На рис.10 справа приведен график зависимости разности численного и аналитического решений в норме от числа узлов сетки в области G(t,x) = [0,1][0,1]. Если число узлов по времени N_t, а по пространству — N_x, то общее число узлов сетки N_tN_x. Из графика видна тенденция уменьшения ошибки в норме по мере роста числа узлов сетки N_tN_x.

Вернемся теперь к условию Куранта в форме (26). Для параметров задачи (27), выбранных в листинге_№7, соотношение Куранта варьировалось в довольно широком диапазоне ( ), при этом проблем с устойчивостью численного решения методом прогонки не наблюдалось.

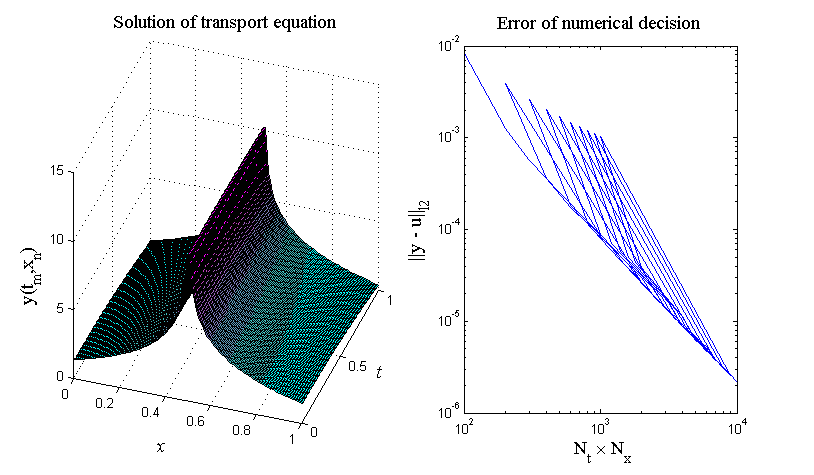
Рис.10.Численное решение задачи (27) (рисунок слева) и зависимость ошибки численного решения в норме от числа узлов сетки в области интегрирования G = [0,T][0,a] (рисунок справа)

Квазилинейное уравнение

Сильные и слабые разрывы. При решении линейного уравнения переноса разрывы в решениях появляются в связи с разрывами либо в начальных, либо в граничных условиях. В квазилинейных уравнениях, даже при наличии гладкости в начальных и граничных условиях, решения могут стать разрывными. Исследуем вопрос об образовании разрывов на примере решения простейшего квазилинейного уравнения

, (28)

которое возникает при одномерном описании движения жидкости и газа. В уравнении переноса (28) скорость переноса определяется самим решением, т.е. c = u(t,x).

В дальнейшем будем рассматривать простейший случай уравнения (28), когда решение u знакопостоянно u(t,x) > 0 и граничное и начальное значения на положительных полуосях системы координат (t,x) полностью определяют решение в первом квадранте. Поскольку граничное и начальное значения передаются по характеристикам x  ut = const, а их наклон зависит от решения, постольку возможны такие начальные данные, при которых характеристики могут пересекаться, что приводит к появлению разрывных решений. С этой точки зрения существует четыре типа начальных данных.

Первый тип начальных данных. Начальные и граничные являются непрерывными функциями такими, что u(0,x) монотонно не убывает, а u(t,0) монотонно не возрастает и они непрерывно согласованы в начале координат.

Наклон (тангенс угла наклона к оси x) характеристик в каждой точке плоскости (t,x) равен 1/u(t,x). При данном типе начальных данных наклон монотонно и непрерывно убывает слева направо (рис.11,а). Первый квадрант всюду плотно покрыт характеристиками и через каждую точку проходит одна и только одна характеристика. По этим характеристикам в данную точку переносится либо граничное, либо начальное значения. Решение однозначно определено и непрерывно во всем квадранте.

Для примера возьмем следующие граничные и начальные условия

,

тогда характеристики, выходящие из точек (t,0), t  [0,T] и (0,x), x  [0,a], в окрестности этих точек удовлетворяют уравнениям:

. (29)

Решая уравнения (29), можно найти два класса приближенных характеристик, выходящих из граничного и начального условий, т.е.

, (30)

где t₀, x₀ — константы, пробегающие значения по отрезку [0,T] и отрезку [0,a] соответственно.

На листинге_№8 приведен код небольшой программы, которая изображает приближенные характеристики (30) в области G = [0,T][0,a]. Итог работы кода программы листинга_№8 приведен на рис.11,а. Стрелка на рис.11,а указывает общее направление переноса граничных и начальных условий.