Листинг_№5
%Программа тестирования схемы без шаблона для
%численного решения уравнения переноса (19)
function witht_template
%Определяем пределы интегрирования уравнения
%переноса по времени и по пространству, [0,T]x[0,a]
T=1; a=1; kmax=400; l=1;
for k=50:50:kmax
%Определяем число узлов сетки по времени и
%по пространству
Nt=k; Nx=k;
%Определяем неравномерную сетку по времени
t(1)=0;
for m=1:(Nt-1)
t(m+1)=t(m)+(T/(Nt-1))*(1+0.1*randn);
end
%Определяем неравномерную сетку по пространству
x(1)=0;
for n=1:(Nx-1)
x(n+1)=x(n)+(a/(Nx-1))*(1+0.1*randn);
end
%Задаем левое граничное условие u(t,0)=-t^2
for m=1:Nt
y(m,1)=-t(m)^2;
end
%Задаем начальные данные u(0,x)=x^2
for n=1:Nx
y(1,n)=x(n)^2;
end
%Организуем цикл расчетов по схеме без шаблона
for m=1:(Nt-1)
tau=t(m+1)-t(m);
for n=2:Nx
c=t(m+1)/x(n); xa=x(n)-c*tau;
p=1;
while (~((xa>=x(p))&(xa<x(p+1))))&((p+1)~=Nx)
p=p+1;
end
if xa>0
%интерполяция
y(m+1,n)=((x(p+1)-xa)/(x(p+1)-x(p)))*...
y(m,p)+((xa-x(p))/(x(p+1)-x(p)))*y(m,p+1);
else
y(m+1,n)=-(t(m)-xa/c)^2;
end
end
end
%Находим различие между численным и
%аналитическим решениями
for m=1:Nt
for n=1:Nx
yerror(m,n)=abs(y(m,n)-ya(t(m),x(n)));
end
end
%Запоминаем ошибку численного решения в норме C
error_without_template(l)=max(max(yerror));
l=l+1;
end
%Рисуем зависимость ошибки численного решения от
%количества узлов сетки по пространству и времени
plot(50:50:kmax,error_without_template,...
'-*','MarkerSize',12);
%Определяем аналитическое решение (20) уравнения переноса
function y=ya(t,x)
y=x^2-t^2;
Знакопеременная скорость переноса c(t,x). В этом случае задача поставлена корректно, когда условия поставлены на тех границах, характеристики из которых идут внутрь области G(t,x).
Пусть скорость
c(t,x)
непрерывна в области G(t,x)
= [0,T][0,a]
и меняет знак на линии
,
т.е.
,
при этом будем считать
,
и
,
.
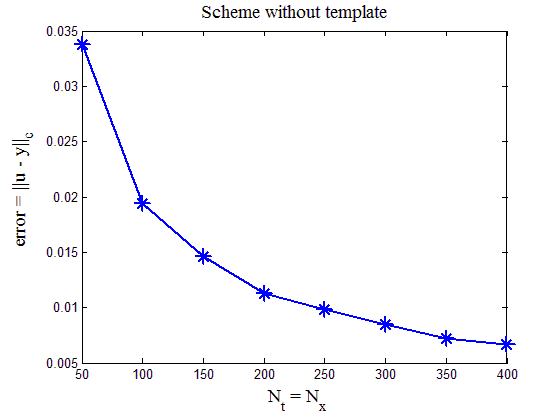
Рис.8. Зависимость ошибки численного решения задачи (19), (20) от числа узлов сетки по времени и пространству для схемы без шаблона
Для примера рассмотрим уравнение переноса следующего вида
(21)
где
.
Найдем вид характеристик для уравнения
(21). Для этого необходимо решить
обыкновенное дифференциальное уравнение
. (22)
Решение уравнения (22) легко найти. Решение содержит две ветви, из которых выбираем положительную (t > 0), т.е.
,
A
= const. (23)
Нарисуем характеристики (23) средствами MATLAB. На листинге_№6 приведен короткий код программы рисования характеристик (23). Итог работы кода программы листинга_№6 приведен на рис.9,а. В целях упрощения кода на рис.9,а нарисованы лишь те характеристики, которые выпущены из левой и правой границ области G(t,x) = [0,T][0,a]. Стрелкой на рис.9,а обозначена линия, на которой скорость переноса обращается в ноль.