Листинг_№4
%Программа сравнения явно-неявной схемы для решения
%уравнения переноса с безусловно устойчивой схемой (7в)
function obvious
%Определяем пределы интегрирования уравнения переноса
%по времени и по пространству, [0,T]x[0,a]
T=1; a=1; kmax=300; l=1;
for k=50:50:kmax
%Определяем число узлов сетки по времени и
%по пространству
Nt=k; Nx=k;
%Определяем неравномерную сетку по времени
t(1)=0;
for m=1:(Nt-1)
t(m+1)=t(m)+(T/(Nt-1))*(1+0.1*randn);
end
%Определяем неравномерную сетку по пространству
x(1)=0;
for n=1:(Nx-1)
x(n+1)=x(n)+(a/(Nx-1))*(1+0.1*randn);
end
%Задаем левое граничное условие u(t,0)=-t^2
for m=1:Nt
y(m,1)=-t(m)^2;
end
%Задаем начальные данные u(0,x)=x^2
for n=1:Nx
y(1,n)=x(n)^2;
end
%Организуем цикл расчетов по явно-неявной
%схеме (15), (15')
for m=1:(Nt-1)
tau=t(m+1)-t(m);
for n=2:Nx
h=x(n)-x(n-1); c=t(m+1)/x(n); r=(tau*c)/h;
if r<=1
y(m+1,n)=(1-r)*y(m,n)+r*y(m,n-1)+...
tau*f(t(m)+0.5*tau,x(n)-0.5*h);
else
y(m+1,n)=(1-1/r)*y(m+1,n-1)+y(m,n-1)/r+...
(tau/r)*f(t(m)+0.5*tau,x(n)-0.5*h);
end
end
end
%Находим различие между численным и
%аналитическим решениями
for m=1:Nt
for n=1:Nx
yerror(m,n)=abs(y(m,n)-ya(t(m),x(n)));
end
end
%Выводим ошибку численного решения в норме C
error_obvious(l)=max(max(yerror));
%Организуем расчет по безусловно устойчивой схеме (7в)
for m=1:(Nt-1)
tau=t(m+1)-t(m);
for n=2:Nx
h=x(n)-x(n-1); c=t(m+1)/x(n); r=(tau*c)/h;
y(m+1,n)=(r/(1+r))*y(m+1,n-1)+y(m,n)/(1+r)+...
(tau/(1+r))*f(t(m)+0.5*tau,x(n)-0.5*h);
end
end
%Находим различие между численным и
%аналитическим решениями
for m=1:Nt
for n=1:Nx
yerror(m,n)=abs(y(m,n)-ya(t(m),x(n)));
end
end
%Выводим ошибку численного решения в норме C
error_non_obvious(l)=max(max(yerror));
l=l+1;
end
plot(50:50:kmax,error_obvious,'-*', ...
50:50:kmax,error_non_obvious,'-p','MarkerSize',12);
%Определяем функцию, возвращающую правую часть уравнения
function y=f(t,x)
y=x^2+2*t^2;
%Определяем аналитическое решение уравнения переноса
function y=ya(t,x)
y=x^2-t^2+x^2*t;
На рис.7 приведен итоговый график сравнения явно-неявной схемы (15), (15) и безусловно устойчивой неявной схемы (7в) на примере решения задачи (16), (17). На графике по оси абсцисс отложено число точек сетки по времени и по пространству, по оси ординат — ошибка как разность численного и аналитического решений в норме . Из графика отчетливо видно, что явно-неявная схема более точна, чем безусловно устойчивая неявная схема.
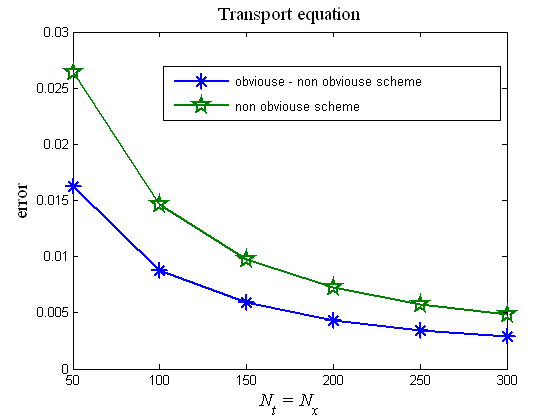
Рис.7. Сравнение ошибок при расчетах по явно-неявной (15), (15) и безусловно устойчивой неявной (7в) разностных схем
Схема без шаблона.
Рассмотрим характеристику, которая
приходит в узел (tm +1,xn)
и которая пересекает слой tm
в точке
.
Найдем пару узлов
на слое tm,
между которыми попадает точка
.
Определим
с помощью линейной интерполяции по
значениям
:
, (18)
при этом
.
Переносим значение
по характеристике в узел (tm +1,xn),
т.е. полагаем
.
В соответствии с геометрическим смыслом
устойчивости, разностная схема (18)
безусловно устойчива.
В разностной схеме
(18) положение пары узлов
и
относительно узла (tm +1,xn)
не определено, когда скорость c
= c(t,x)
не фиксирована или сетка по пространству
не равномерна. Это означает, что разностная
схема (18) является схемой без шаблона.
Изучим поведение точности схемы (18) на примере решения задачи:
(19)
Решение задачи (19) можно легко найти
. (20)
На листинге_№5 приведен код программы, которая с помощью схемы без шаблона численно решает задачу (19). На выходе работы программы строится график ошибки численного решения error = в зависимости от числа узлов сетки по времени и по пространству (Nt = Nx). Данный график приведен на рис.8. График на рис.8 демонстрирует “правильное” поведение ошибки, она уменьшается по мере роста числа узлов одновременно по времени и по пространству.