Листинг_№3

%Программа численного решения уравнения

%переноса du/dt+cdu/dx=tx

%u(0,x)=x^3/(12c^2), u(t,0)=(ct^3)/12 и

%сравнение его с аналитическим решением

function schm4_conv

global c

%определяем параметр скорости переноса c,

%а также отрезок времени интегрирования T и

%диапазон изменения пространственной

%переменной a

c=0.25; T=2; a=1; h=0.2;

%определяем количество делений шага h пополам

kmax=7;

for k=1:kmax

%делим шаг h пополам

h=h/2;

%определяем шаг по времени, который считается

%пропорциональным шагу по пространству

tau=0.5*h/c; r=(c*tau)/h;

%определяем сетки по времени и по пространству

t=0:tau:T; x=0:h:a;

%определяем начальное значение u(0,x)=x^3/(12c^2)

for j=1:length(x)

y(1,j)=x(j)^3/(12*c^2);

end

%организуем расчет по разностной схеме (7г)

for i=1:(length(t)-1)

%определяем левое граничное значение

%u(t,0)=(ct^3)/12

y(i+1,1)=(c*t(i+1)^3)/12;

for j=2:length(x)

y(i+1,j)=((r-1)/(r+1))*...

(y(i+1,j-1)-y(i,j))+y(i,j-1)+...

2*(tau/(r+1))*(t(i)+0.5*tau)*(x(j)-0.5*h);

end

end

for i=1:length(t)

for j=1:length(x)

yt(i,j)=abs(y(i,j)-ya(t(i),x(j)));

end

end

s=0;

for i=2:(length(t)-1)

for j=2:(length(x)-1)

s=s+tau*h*(y(i,j)-ya(t(i),x(j)))^2;

end

end

step(k)=h;

%оцениваем ошибку численного решения в нормах

%l2 и C и делим эти оценки на квадрат шага h^2

constl2(k)=max(max(yt))/h^2;

constC(k)=sqrt(s)/h^2;

end

%рисуем зависимость предстепенной константы в

%оценке ошибки от шага сетки h

plot(step,constl2,'-*',step,constC,'-p','MarkerSize',12);

%функция, возвращающая аналитическое решение

function z=ya(t,x)

global c

z=(1/(8*c^2))*(x+c*t)*((x+c*t)^2/3-(x-c*t)^2);

if (x-c*t)>=0

z=z+(x-c*t)^3/(6*c^2);

else

z=z-(x-c*t)^3/(6*c^2);

end

На рис.5 приведен итог работы программы листинга_№3. Отчетливо видно, что и в норме , и в норме численное решение по разностной схеме (7г) сходится к аналитическому решению со вторым порядком точности по  и h.

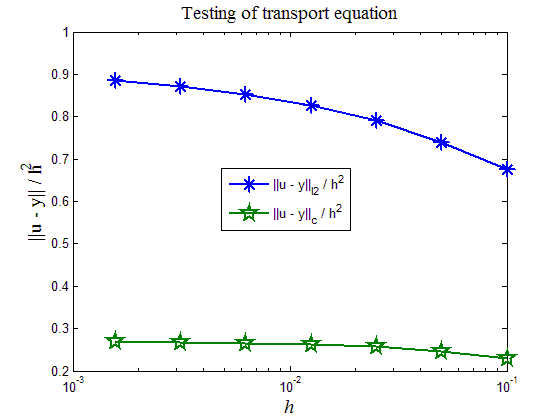
Рис.5. Зависимости предстепенных констант в оценках ошибок численного решения для двух норм

Геометрическая интерпретация устойчивости

Дадим геометрическую интерпретацию устойчивости по начальным данным. Для простоты рассмотрим однородное уравнение (3), т.е. при f(t,x) = 0. Общее решение однородного уравнения переноса имеет вид (4): , т.е. значения решения переносятся вдоль характеристики x  ct = const без изменения.

Рассмотрим разностную схему (7а) с шаблоном на рис.6,а (аналогичный шаблон приведен на рис.2,а). На рис.6,а стрелкой обозначена характеристика, приходящая в точку (t_m +1,x_n). Характеристика пересекает слой t_m в точке . Точка пересечения находится согласно определению характеристики: = const.

Рис.6,а. Перенос значения функции по характеристике при выполнении условия Куранта (для схемы (7а))	Рис.6,б. Перенос значения функции по характеристике при нарушении условия Куранта (для схемы (7а))	Рис.6,в. Перенос значения функции по характеристике при любых значениях  и h (для схемы (7в))

Найдем решение в точке с помощью линейной интерполяции разностного решения между двумя узлами шаблона рис.6,а на слое t_m, тогда

.

Далее полученное значение из точки переносим без изменения по характеристике в узел (t_m +1,x_n), т.е. положим .

Выполнение условия устойчивости для схемы (7а) c  h обеспечивает попадание точки в полуинтервал [x_n 1,x_n), т.е. . Если условие устойчивости нарушается, точка становится меньше x_n 1, т.е. при c > h. В этой ситуации решение в точке находится с помощью экстраполяции. Другими словами, схема (7а) устойчива, если вычисляется по значениям с предыдущего слоя при помощи интерполяции (рис.6,а). Схема (7а) неустойчива, если при вычислении величины используется экстраполяция (рис.6,б).

Разностные схемы (7б), (7в) можно также интерпретировать как линейные интерполяции по двум уже вычисленным значениям с переносом полученного значения по характеристике. Так, безусловная устойчивость схемы (7в) обязана тому, что приходящая в узел (t_m +1,x_n) характеристика при любых  и h пересекает отрезок (пунктирная линия на рис.6,в), соединяющий узлы интерполяции значения решения, которое по характеристике переносится в узел (t_m +1,x_n).

Разностная схема (7г) также может быть истолкована как интерполяция, но не двухточечная, а трехточечная. Учитывая рис.2,г видно, что при любом выборе шагов  и h приходящая в узел (t_m +1,x_n) характеристика переносит значение, которое вычисляется с помощью интерполяции по ранее вычисленным значениям.

Данная геометрическая интерпретация полезна тем, что по имеющейся характеристике можно подобрать шаблон разностной схемы так, чтобы было выполнено требование устойчивости. Рассмотрим некоторые примеры.

Явно-неявная схема. Будем считать, что шаг по времени и по пространству не постоянны, а скорость переноса переменная величина, т.е. c = c(t,x). При вычислении проверим условие Куранта (8) в текущей ячейке. Если условие Куранта выполняется, то используем схему (7а):

, (15)

если условие Куранта в форме (8) нарушается, используем схему (7б):

. (15)

Явно-неявная схема (15), (15) безусловно устойчива, причем невязка этой схемы меньше, чем у безусловно устойчивой схемы (7в). Схему (15), (15) используют в том случае, когда искомое решение является недостаточно гладким или быстропеременным.

Сравним разностные схемы (15), (15) и (7в) на примере решения задачи:

(16)

Решение задачи (16) можно легко найти

. (17)

На листинге_№4 приведен код программы численного решения задачи (16) и сравнения полученного решения с аналитическим решением (17). Сравнение производится в норме , т.е. error = .