Листинг_№1
%Программа численного решения уравнения
%переноса du/dt+cdu/dx=tx
%u(0,x)=x^3/(12c^2), u(t,0)=(ct^3)/12
%очищаем рабочее пространство
clear all
%определяем параметр скорости переноса c,
%а также отрезок времени интегрирования T и
%диапазон изменения пространственной
%переменной a
c=0.25; T=2; a=1;
%определяем шаг по пространству
h=0.005;
%рассматривается два варианта расчета
%при tau=h/c (условие Куранта выполняется) и
%при tau=1.12*h/c (условие Куранта нарушено)
tau=(1.0*h)/c;
r=(c*tau)/h;
%определяем сетки по времени и по пространству
t=0:tau:T;
x=0:h:a;
%определяем начальное значение u(0,x)=x^3/(12c^2)
for j=1:length(x)
y(1,j)=x(j)^3/(12*c^2);
end
%организуем расчет по разностной схеме (7а)
for i=1:(length(t)-1)
%определяем левое граничное значение
%u(t,0)=(ct^3)/12
y(i+1,1)=(c*t(i+1)^3)/12;
for j=2:length(x)
y(i+1,j)=(1-r)*y(i,j)+r*y(i,j-1)+...
tau*(t(i)+0.5*tau)*(x(j)-0.5*h);
end
end
[xi ti]=meshgrid(x,t);
%рисуем численное решение уравнения переноса u(t,x)
surf(ti,xi,y); [xi ti]=meshgrid(x,t);
%рисуем численное решение уравнения переноса u(t,x)
surf(ti,xi,y);
|
|
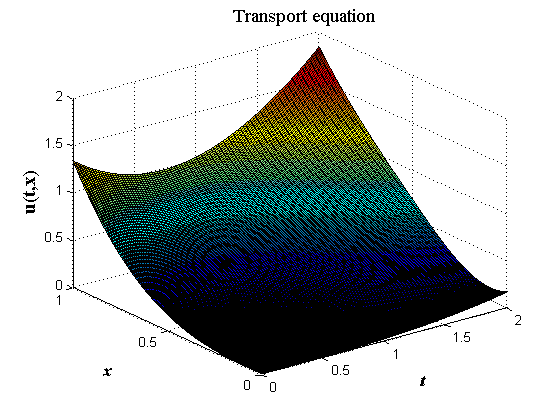
Рис.3,а. Численное решение уравнения (10) по разностной схеме (7а) при выполнении условия Куранта |
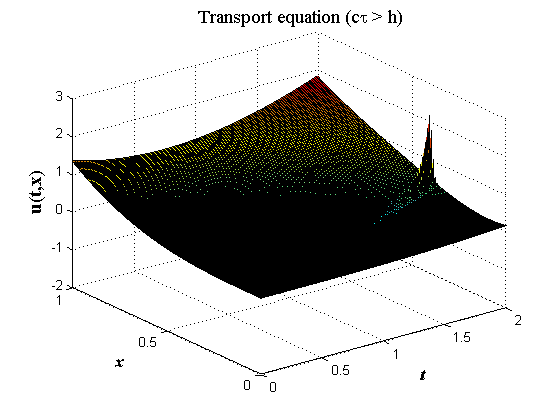
Рис.3,б. Численное решение уравнения (10) по разностной схеме (7а) с нарушением условия Куранта (8) |
Сравним теперь
численное решение задачи (10) и аналитическое
решение (11). На листинге_№2 приведен код
соответствующей программы. В программе
считается, что
= 0.5h/c
и варьируется шаг по пространству. На
рис.4 приведен итог работы кода программы
листинга_№2 в виде кривой зависимости
отношения ошибки численного решения к
шагу сетки const(h)
=
в зависимости от шага сетки h.
Из условия аппроксимации разностной
схемой (7а) исходного уравнения (3) с
порядком O(
+ h)
следует, что величина const(h)
должна стремиться к некоторой константе
по мере того, как h
0. Такая тенденция видна на рис.4.
Листинг_№2
%Программа численного решения уравнения
%переноса du/dt+cdu/dx=tx
%u(0,x)=x^3/(12c^2), u(t,0)=(ct^3)/12 и
%сравнение его с аналитическим решением
function schm1_conv
global c
%определяем параметр скорости переноса c,
%а также отрезок времени интегрирования T и
%диапазон изменения пространственной
%переменной a
c=0.25; T=2; a=1; h=0.2;
%определяем количество делений шага h пополам
kmax=7;
for k=1:kmax
%делим шаг h пополам
h=h/2;
%определяем шаг по времени, который считается
%пропорциональным шагу по пространству
tau=0.5*h/c; r=(c*tau)/h;
%определяем сетки по времени и по пространству
t=0:tau:T; x=0:h:a;
%определяем начальное значение u(0,x)=x^3/(12c^2)
for j=1:length(x)
y(1,j)=x(j)^3/(12*c^2);
end
%организуем расчет по разностной схеме (7а)
for i=1:(length(t)-1)
%определяем левое граничное значение
%u(t,0)=(ct^3)/12
y(i+1,1)=(c*t(i+1)^3)/12;
for j=2:length(x)
y(i+1,j)=(1-r)*y(i,j)+r*y(i,j-1)+...
tau*(t(i)+0.5*tau)*(x(j)-0.5*h);
end
end
for i=1:length(t)
for j=1:length(x)
yt(i,j)=abs(y(i,j)-ya(t(i),x(j)));
end
end
step(k)=h;
%определяем ошибку численного решения в норме C
%и делим ее на шаг сетки h
const(k)=max(max(yt))/h;
end
%рисуем зависимость предстепенной константы от
%шага сетки h
plot(step,const,'-*','MarkerSize',12);
%функция, возвращающая аналитическое решение
function z=ya(t,x)
global c
z=(1/(8*c^2))*(x+c*t)*((x+c*t)^2/3-(x-c*t)^2);
if (x-c*t)>=0
z=z+(x-c*t)^3/(6*c^2);
else
z=z-(x-c*t)^3/(6*c^2);
end
Разностная схема (7б) исследуется аналогично. Для исследования аппроксимации разложение в ряд Тейлора удобно проводить в окрестности узла (xn 1,tm + ). Для дважды непрерывно дифференцируемого решения данная схема при выполнении условия устойчивости
c h (12)
обеспечивает сходимость со скоростью O( + h).
Разностная схема (7в) безусловно устойчива и на дважды непрерывно дифференцируемых решениях сходится к точному решению со скоростью O( + h).
Разностная схема
(7г) симметричная и следует ожидать, что
порядок ее аппроксимации выше, чем в
предыдущих членах. Для оценки порядка
аппроксимации разложение в ряд Тейлора
удобно провести в окрестности центра
ячейки
.
После проведения соответствующих
выкладок, можно найти оценку невязки:
. (13)
Тем самым схема (7г) имеет второй порядок аппроксимации, когда решения имеют непрерывные производные вплоть до третьей.
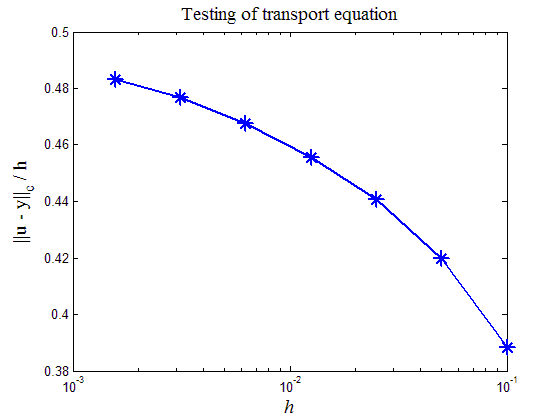
Рис.4. Зависимость предстепенной константы в оценке ошибки численного решения от шага сетки
Устойчивость разностной схемы (7г) исследуем с помощью метода разделения переменных. Подставляя в (7г)
,
найдем значение коэффициента роста Фурье-гармоники при переходе со слоя на слой:
. (14)
Из оценки (14)
следует, что
для любой гармоники и при любых
соотношениях шагов. Это означает, что
схема (7г) безусловно и равномерно
устойчива по начальным данным в норме
.
Исследуем разностную
схему (7г) на предмет сходимости в двух
нормах:
и
.
На листинге_№3 приведен код программы
для изучения сходимости схемы (7г) на
примере численного решения задачи (10)
и сравнения полученного решения с
аналитическим решением (11). В программе
вычисляются зависимости предстепенных
констант const(h)
для двух норм от шага сетки h,
при этом считается, что
= 0.5h/c.
Согласно теоретическим оценками,
предстепенная константа const(h)
=
должна выходить на некоторое постоянное
значение при h
0.