Листинг_№11
%Программа сравнения разностных схем (49), (50')
%на примере динамики образования ударной волны
%Очищаем рабочее пространство
clear all
%Задаем пределы области интегрирования G=[0,T]x[0,a]
T=3; a=3;
%Задаем параметры сетки по времени и пространству
tau=0.002; h=0.01; r=tau/h;
%Задаем сетки по времени и пространству
t=0:tau:T; x=0:h:a;
Nt=length(t); Nx=length(x);
%Определяем левое граничное условие u(t,0)=0
for m=1:Nt
y(m,1)=0;
end
%Определяем начальное условие u(0,x)=sin(pi x)^2,
%0<=x<=1; u(0,x)=0, 1<x<=a
for n=1:Nx
if x(n)<=1
y(1,n)=sin(pi*x(n))^2;
else
y(1,n)=0;
end
end
%Организуем цикл расчета по схеме (49) на различные
%моменты времени
for m=1:(Nt-1)
for n=2:Nx
y(m+1,n)=y(m,n)-r*(y(m,n)^2-y(m,n-1)^2);
end
end
%Рисуем профили волны в различные моменты времени на
%одном и том же графике в координатах решение -
%пространственная координата
for m=1:35:Nt
subplot(1,2,1);
plot(x,y(m,:));
hold on
end
%Организуем цикл расчета по схеме (50') на различные
%моменты времени
for m=1:(Nt-1)
for n=2:Nx
y(m+1,n)=-1/r+sqrt(1/r^2+(2/r)*y(m,n)+y(m+1,n-1)^2);
end
end
%Рисуем профили волны в различные моменты времени
for m=1:35:Nt
subplot(1,2,2);
plot(x,y(m,:));
hold on
end
На рис.15 приведен итог работы кода программы листинга_№11. Образовавшиеся ударные волны довольно сильно отличаются друг от друга при расчетах по схеме (49) (левый график на рис.15) и по схеме (51) (правый график на рис.15). Отличия связаны с разными амплитудами ударных волн и с разной скоростью их распространения. Отметим, что таких явных отличий для ударных волн на рис.14, полученных по схемам (40), (45), не просматривается.
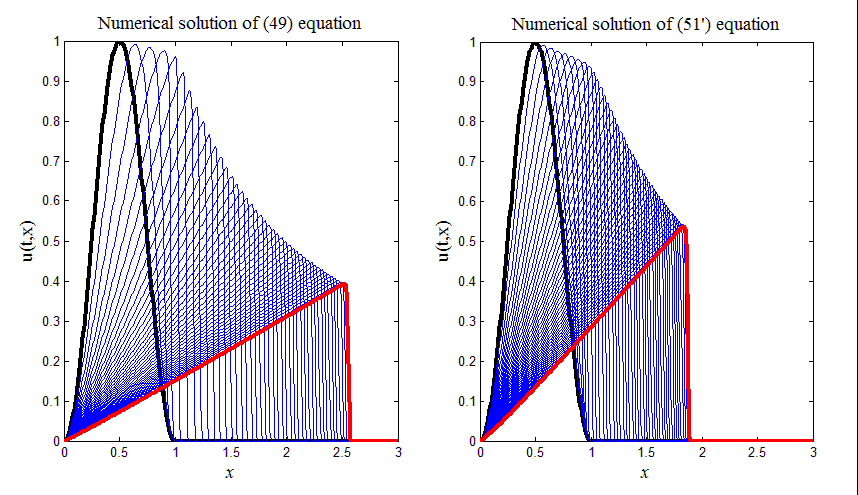
Рис.15. Изучение механизма образования ударной волны на примере решения квазилинейного уравнения переноса с помощью разностных схем (49), (51)
Устойчивость называется безусловной, если ее определение выполняется при произвольном соотношении шагов по различным переменным (при условии достаточной малости шагов). Если определение устойчивости обеспечивается дополнительным соотношением, то устойчивость называется условной.
Это довольно грубые схемы аппроксимации
интеграла по формулам:
,
.
На равномерной сетке эти схемы дают
первый порядок точности O(h).
—