Характеристика системы массового обслуживания с неограниченным ожиданием.
Системы, в которых, с одной стороны, возникают массовые запросы (требования) на выполнение каких-либо видов услуг, а с другой стороны, происходит удовлетворение этих запросов, называются системами массового обслуживания.
Системы массового обслуживания, у которых возможно появление как угодно длинной очереди требований к обслуживающему устройству, называются системами с ожиданием.
Если время ожидания заявки в очереди ничем не ограничено, то система называется «чистой системой с ожиданием». Если оно ограничено какими-то условиями, то система называется «системой смешанного типа». Это промежуточный случай между чистой системой с отказами и чистой системой с ожиданием.
Основные понятия смо:
Требование (заявка) — запрос на обслуживание.
Входящий поток требований — совокупность требований, поступающих в СМО.
Время обслуживания — период времени, в течение которого обслуживается требование.
Математическая модель СМО — это совокупность математических выражений, описывающих входящий поток требований, процесс обслуживания и их взаимосвязь.
системы с потерями, в которых требования, не нашедшие в момент поступления ни одного свободного прибора, теряются;
системы с ожиданием, в которых имеется накопитель бесконечной ёмкости для буферизации поступивших требований, при этом ожидающие требования образуют очередь;
системы с накопителем конечной ёмкости (ожиданием и ограничениями), в которых длина очереди не может превышать ёмкости накопителя; при этом требование, поступающее в переполненную СМО (отсутствуют свободные места для ожидания), теряется.
Характеристика системы массового обслуживания с ограниченной длиной очереди.
Системы, в которых, с одной стороны, возникают массовые запросы (требования) на выполнение каких-либо видов услуг, а с другой стороны, происходит удовлетворение этих запросов, называются системами массового обслуживания.
Системы массового обслуживания, допускающие очередь, но с ограниченным числом мест в ней, называются системами с ограниченной длиной очереди.
Основные понятия смо:
Требование (заявка) — запрос на обслуживание.
Входящий поток требований — совокупность требований, поступающих в СМО.
Время обслуживания — период времени, в течение которого обслуживается требование.
Математическая модель СМО — это совокупность математических выражений, описывающих входящий поток требований, процесс обслуживания и их взаимосвязь.
системы с потерями, в которых требования, не нашедшие в момент поступления ни одного свободного прибора, теряются;
системы с ожиданием, в которых имеется накопитель бесконечной ёмкости для буферизации поступивших требований, при этом ожидающие требования образуют очередь;
системы с накопителем конечной ёмкости (ожиданием и ограничениями), в которых длина очереди не может превышать ёмкости накопителя; при этом требование, поступающее в переполненную СМО (отсутствуют свободные места для ожидания), теряется.
Графы. Основные определения. Применение графов при решении задач исследования операций.
В некоторых практических ситуациях для наочности удобно использовать схемы, которые называют графами. Граф состоит с однородных объектов, которые называются узлами (англ. - node) и линий, которых называют дугами (англ. - arc), и связывают пары узлов между собой. Эти объекты – узлы и дуги – могут исполнять только роль схемы, определяя связи, в других случаях они имеют определенные характерные оценки, которые соответствуют поставленной задаче. В ориентированном графе эти линии имеют вид стрелок, указывая на ориентацию между узлами. Подобная сетевая схема используется для наочного представления транспортной задачи с узлами-поставщиками и узлами-потребителями, где направленные дуги у виде стрелок определяют возможные маршруты перевозок (потоков):
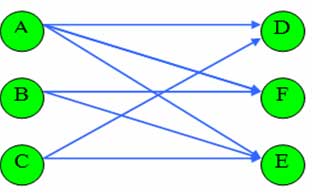
Ключевое слово «поток» определило в математическом программирование класс моделей потокового программирования (сетевого). Формирование этого направления припадает на 60-е года ХХ в. определено публикацией фундаментальной роботы Дж. Данцига, Л. Форда и Д. Фалкерсона. Оказалось, что если задачу можноа подать в графической форме в виде сетки, тогда можно с помощью довольно эффективных потоковых алгоритмов получить ее оптимальное решение на основе математических графов с меньшими затратами компьютерных ресурсов. Ориентированный граф называют сеткой (network), где определяют:
внешний узел-источник, который имеет только выходящие дуги;
внешний узел-сток, который имеет только входящие дуги;
все остальные узлы – внутренние (промежуточные, транзитные) , у которых есть входящие и выходящие дуги, которые связывают узлы.
Для дуги могут быть такие характеристики: пропускная способность канала, расстояние между парой узлов, стоимость перевозок, вероятность прохождения сигнала по цепи, количество необходимых ресурсов для исполнения операции и т. д. Поскольку задачи на графах относят к оптимизационных задач, они составляют самостоятельный и очень распространенный класс сетевых моделей оптимизации. Дуга со стрелкой и определенным значением соответственного параметра определяет универсальное понятие – поток (flow), что движется с начального узла в конченый. Объектом потоков в практических задачах выступают жидкость, груз, сигналы связи, темп исполнения операций из залученных ресурсов, энергия, газ, пассажиры, капитал, транспортные средства и тому подобное. Способы представления сетки в Еxcel:
Матрица смежности – квадратная матрица связи типа «каждый-с-каждым» размером n?n, де n – число узлов. Элемент такой матрицы принимает не нулевое значение (расстояние, затраты), если существует дуга между узлами, или 0 в противоположном случае. Эта матрица полностью определяет структуру сетки. Для анализа и расчётов используется аппарат матричной и линейной алгебры. Этот способ используется при решении классической транспортной задачи, задачи коммивояжера, то есть там, где количество дуг значительно превышает количество узлов. Например, для описания графа, который состоит из 15 узлов и, соответственно, 225 дуг, лучше применить матрицу для компактной записи данных.
Вектор координат и характеристик коэффициентов дуг – таблица с трех и больше столбцов (начало дуги, конец дуги, одна и больше характеристик дуги, например, ее длина) и строк. Этот способ применяют там, где число узлов и дуг приблизительно одинаковое. Например, в сетевой транспортной задаче с промежуточными пунктами лучше и более естественно использовать векторную форму представления транспортной сети, чем матричную.
Для сетевых моделей оптимизации фундаментальным есть принцип сохранения потока в любом узле (экономисты называют это балансом), а именно: сума потоков на выходе узла равно суме потоков на его входе плюс потенциал узла (+предложение/ -спрос).