1.5 Выбор средства измерения с позиции
обеспечения необходимой точности
Для того чтобы выбрать СИ, требуется определить необходимую точность проводимого измерения. Определим необходимую точность на основе анализа измерительной схемы:
;
Из вышеприведенной формулы выразим допустимую погрешность СИ:
;
Теперь осталось вычислить полученные выражения.
;
;
;
;
;
;
;
Таким образом, для регистрации допуска
торцевого биения с погрешностью в 50 мк
должно быть выбрано СИ с погрешностью
измерения не более 14,009 мк. Таким
является прибор Головка рычажно-зубчатая
ИТ с
при интервале измерений в (120÷180) мм.
2. Оценка достоверности контроля
2.1 Понятие о вероятностных ошибках I и II рода,
причины их возникновений
Поскольку измерения выполняются в условиях помех, то о результатах можно говорить с некоторой вероятностью. Выдвигаемая гипотеза может быть правильной или не правильной, поэтому возникает необходимость ее проверки. Поскольку проверку производят статистическими методами, ее называют статистической. В итоге статистической проверки гипотезы в двух случаях может быть принято неправильное решение, т.е. могут быть допущены ошибки двух родов:
Ошибка первого рода
– ошибка, состоящая в отбрасывании
нулевой гипотезы, поскольку статистика
принимает значение, принадлежащее
критической области, в то время как эта
нулевая гипотеза верна.
Вероятность ошибки первого рода – вероятность допустить ошибку первого рода.
Ошибка второго рода
– ошибка принять нулевую гипотезу,
поскольку статистика принимает значение,
не принадлежащее критической области,
в то время как нулевая гипотеза не верна.
Вероятность ошибки второго рода – вероятность допустить ошибку второго рода.
Очевидно, что вероятность правильного решения о процедуре контроля (достоверность решения) вычисляется как:
Оценка вероятностных ошибок осуществляется в области безразмерных величин. Введем следующие обозначения:
– безразмерная величина, характеризующая
истинное значение погрешности
контролируемого параметра, т.е. отклонение
от
номинального значения.
Очевидно, что при попадании параметра в допуск, справедливо следующее неравенство:
– безразмерная величина, пропорциональная
текущей ошибке измерения
(в данном случае находится пределах
).
При выполнении измерений на результате
сказывается и величина отклонения
параметра от номинала и ошибка средства
измерения, т.е. формируется видимое
значение контролируемого параметра,
которое через безразмерные величины
можно характеризовать как
.
Величины ξ и η являются случайными и взаимонезависимыми, и они характеризуется функциями распределения:
где
-
плотность распределения случайной
величины
.
где
-
плотность распределения случайной
величины
.
Совместная функция распределения суммы двух случайных величин и :
(формула 2.1)
-
совместная плотность распределения
случайной величины.
Поскольку ξ и η являются взаимонезависимыми случайными величинами, совместная плотность распределения может быть представлена:
Тогда соотношение (2.1) можно записать:
Ошибка I рода.
Ошибка I рода имеет место при условии, что контролируемый параметр находится в поле допуска ξ ≤ 1, а видимые значения ξ + η > 1 фиксируют выход за пределы допуска
Область интегрирования двумерной функции распределения в этом случае может быть отражена графически.
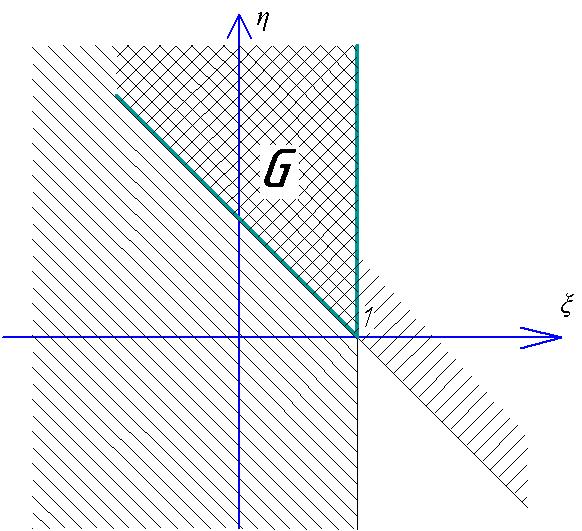
Рисунок 1.7 Область интегрирования ошибки I рода
Из рисунка следует, что ошибка первого рода составляет:
Ошибка II рода
Ошибка II рода имеет место при условии
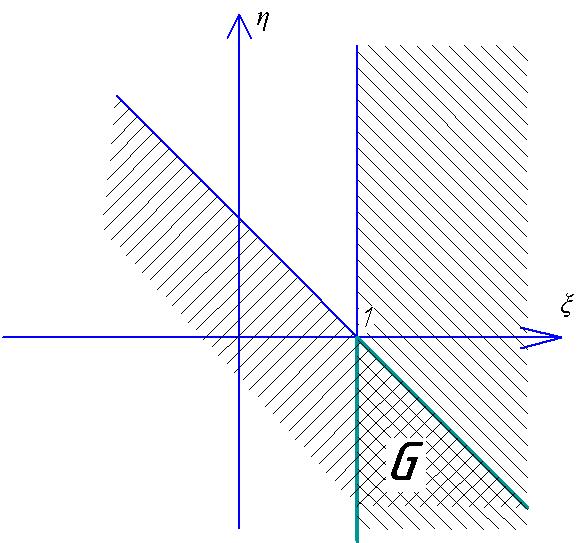
Рисунок 1.8 Область интегрирования ошибки II рода
